гидромеханика. Решение Составляем уравнение Бернулли для сечений 11 и 22, относительно плоскости сравнения 00, проходящей по оси горизонтального участка трубопровода(рис. 20. 1)
 Скачать 230.3 Kb. Скачать 230.3 Kb.
|
 Составляем уравнение Бернулли относительно плоскости 1-1 Z1+p1/rg+av1^2/2g=z2+p2/rg+av2^2/2g Где z1 = H + h , z 2 = 0, p1=p2=pa, v1=v2=0 Решение Составляем уравнение Бернулли для сечений 1-1 и 2-2, относительно плоскости сравнения 0-0, проходящей по оси горизонтального участка трубопровода(рис. 6.20.1): 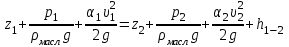 (1) (1)где 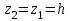 , , 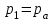 , , 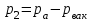 , , 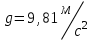 - ускорение свободного падения, - ускорение свободного падения, 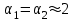 , считая режим движения ламинарным, , считая режим движения ламинарным, 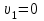 , , 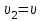 , , 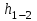 - суммарные потери напора. В процессе решения задачи режим движения масла будет проверен. - суммарные потери напора. В процессе решения задачи режим движения масла будет проверен. 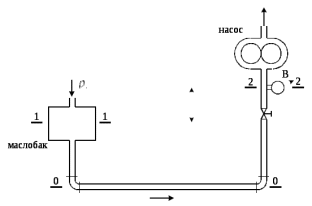 Рис. 6.20.1 После подстановки всех параметров уравнение Бернулли принимает вид 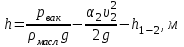 (2) (2)Скорость движения масла: 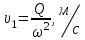 (3) (3)где 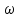 - площадь поперечного сечения трубопровода, - площадь поперечного сечения трубопровода, 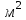 ; ;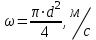 (4) (4)Подставляя выражение (4) в выражение (3) получаем 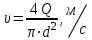 (5) (5)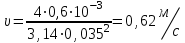 Критерий Рейнольдса: 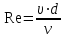 (6) (6)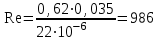 Так как число 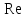 меньше критического значения меньше критического значения 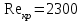 , то режим течения ламинарный, следовательно, принятое значение , то режим течения ламинарный, следовательно, принятое значение 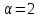 верно. верно.Суммарные потери напора: 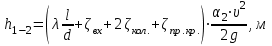 (7) (7)где 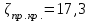 - коэффициент сопротивления пробкового крана с углом закрытия - коэффициент сопротивления пробкового крана с углом закрытия  (справочные данные); (справочные данные);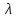 - коэффициент гидравлического трения, который для ламинарного режима определяется по формуле; - коэффициент гидравлического трения, который для ламинарного режима определяется по формуле;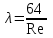 (8) (8)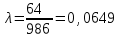 тогда 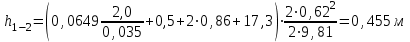 Подставляя полученные значения в формулу (2) находим высоту на которой следует установить шестеренчатый насос системы смазки 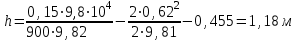 Ответ: высота установки насоса 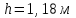 . . |
