олимпиада. Решение. Так как 35%0,35, то вторая бригада должна вспахать на 0,35
 Скачать 77.19 Kb. Скачать 77.19 Kb.
|
|
Одна тракторная бригада должна была вспахать 240 га, а другая на 35 % больше, чем первая. Вспахивая ежедневно на 3 га меньше второй бригады, первая всё же закончила работу на 2 дня раньше, чем вторая. Сколько гектаров вспахивала первая бригада ежедневно? Пусть первая бригада вспахивает х гектаров ежедневно. Укажите номер уравнения, которое позволяет найти х. Решение. Так как 35%=0,35, то вторая бригада должна вспахать на 0,35.240=84 (га) больше, чем первая, то есть вспахать всего 240+84=324 (га). Пусть первая бригада вспахивает x гектаров ежедневно. Составим таблицу.
Вторая бригада на выполнение работы тратит на 2 дня больше, чем первая бригада. Составим уравнение. 324:(x+3)- 240:x=2 162:(x+3)- 120:x=1 Моторная лодка прошла по течению реки 36 км, а против течения 48 км, затратив на весь путь столько времени, сколько надо на прохождение 90 км по озеру. Найдите собственную скорость лодки, если скорость лодки равна 3 км/ ч? Пусть собственная скорость лодки составляет x км/ч. Укажите номер уравнения, которое позволяет найти х. Пусть собственная скорость лодки - х км/ч. Следовательно скорость по течению реки составляет х + 3 км/ч, а против него х - 3 км/ч. Время, которое затратила лодка на движение по течению составляет: 36/(х + 3) ч, а против него 48/(х - 3) ч. Время, за которое лодка прошла бы 90 км по озеру составляет 90/х ч. Составим уравнение: 36/(х + 3) + 48/(х - 3) = 90/х; Теплоход прошёл расстояние между двумя пристанями по течению реки за 7 ч, а против течения – за 9 ч. Определить расстояние между пристанями, если скорость течения реки 2 км/ч. Составьте математическую модель по условию текстовой задачи, обозначив за х км/ч. собственную скорость теплохода. Бассейн наполняется двумя трубами за 2 часа 55 минут. Первая труба может наполнить его на 2 часа быстрее, чем вторая. Укажите номер уравнения, которое позволяет найти 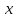 – производительность второй трубы. – производительность второй трубы.Пусть за х часов наполняет бак вторая труба одна тогда ( х-2) часа наполняет бак одна первая труба 1/х часть бассейна наполняет в час первая труба 1/ (х-2) часть бассейна наполняет в час вторая труба 2 часа 55 мин = 35/12 часа 1 : (35/12) = 12/35 часть бассейна наполняют обе трубы за час уравнение 1/ х +1/(х-2) = 12/35 Моторная лодка прошла против течения реки 221 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 15 км/ч. Пусть х км/ч – скорость течения реки. Укажите номер уравнения, которое позволяет найти х. V(Км/ч) S(км) T(ч) Лодка туда х-4 221 221/х-4 Лодка обратно х+4 221 221/(х+4)-2 Решение: 221/х-4 - 221/х+4=2 Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 204 км. На следующий день он отправился обратно со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Пусть х км/ч – первоначальная скорость велосипедиста. Составьте математическую модель по условию текстовой задачи. Скорость из А в В х Проехал 204/х часов Скорость из В в А х+5 Проехал 204/(х+5) часов Разница 204/х - 204/(х+5) = 5 Один рабочий выполняет некоторую работу за 24 дня, другой рабочий ту же работу может выполнить за 48 дней. За сколько дней будет выполнена эта работа, если рабочие будут работать вместе? Выберете математическую модель, которая соответствует условию текстовой задачи.  На двух станках за 4 часа обработали 80 деталей, причём на 1-ом станке обрабатывали на 2 детали в час больше, чем на втором. Обозначьте буквой х количество деталей, обработанных за 1 час на 1-ом станке и составьте уравнение по условию задачи х-в час на 1,х+2-в час на 2 4(х+х+2)*4=80 2х+2=80/4 2х+2=20 Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше? Укажите номер уравнения, которое позволяет найти х– производительность второго рабочего. Второй делает x деталей в час, первый x+1 деталь в час. Первый выполнит заказ на 156 деталей за 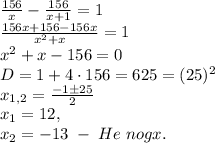 Второй рабочий делает 12 деталей в час. Паша набирает 600 символов на 30 секунд быстрее, чем Даша – 450 символов. Паша за минуту печатает на 90 символов больше, чем Даша. Укажите номер уравнения, которое позволяет найти х – кличество символов, которое набирает Паша за 1 минуту. Пусть х – символов в минуту набирает Паша, а Даша – (х-90) символов в минуту. Паша будет набирать текст 600/х минут, Даша: 450/(х-90) минут. Разница во времени – 30 минут (0,5 часа) . Составим уравнение: 450/(х – 90) – 600/х = 0,5 |
