Вариант 4 доделать. Решение Тогда наращенную сумму по схеме простых процентов можно будет определять следующим образом

• Название: Решение Тогда наращенную сумму по схеме простых процентов можно будет определять следующим образом
• Дата: 11.05.2018
• Размер: 55.16 Kb.
• Имя файла: Вариант 4 доделать.docx
• Тип: Решение; #43396

Вариант 4

1. Предприниматель взял в банке ссуду на 3 года под процентную ставку 25% годовых. Определить, во сколько раз к концу срока сумма долга будет больше выданной банком суммы, если банк начисляет простые проценты.

Решение:

Тогда наращенную сумму по схеме простых процентов можно будет определять следующим образом:

FV = PV + I = PV + i • PV • n = PV (1 + i • n)

где i — процентная ставка

n — количество периодов начисления.

Данная формула называется «формулой простых процентов».

FV= PV*(1+0,25*3)= PV*1,75

Ответ: К концу срока сумма долга будет больше выданной банком суммы в 1,75 раза.

2. Векселедержатель 1 октября предъявил для учета вексель на сумму 600 тыс. руб. со сроком погашения 25 октября текущего года. Банк учел вексель по простой учетной ставке 20 % годовых. Какую сумму получит векселедержатель от банка?

Решение:

Рассчитаем сумму, которую получит векселедержатель от банка по формуле:

P=F(1-t/Td),
где F – стоимость векселя;
t – продолжительность финансовой операции в днях;

Т - количество дней в году;

d – учетная ставка;

P=600∙(1-24/365∙0,2)=592,11 тыс. руб.

Таким образом, владелец векселя получит 592,11 тыс. руб.

3. Банк предоставил ссуду в размере 500 тыс. руб. на 33 месяца под процентную ставку 28 % годовых на условиях ежегодного начисления процентов. Какую сумму нужно будет вернуть банку по окончании срока при использовании следующих условий: 1) при расчетах используется схема сложных процентов; б) при расчетах используется смешанная схема?
Решение:

1) Определим сумму, которую необходимо вернуть банку по окончании срока при использовании схемы сложных процентов:



где P – первоначальный размер ссуды;

r – процентная ставка;

w – число лет.



2) Определим сумму, которую необходимо вернуть банку по окончании срока при использовании смешанной схемы начисления процентов:

F = P(1 + r)^w.(1 + f∙r),

где f- целая часть периода финансовой операции/

F = 500∙(1 + 0,28)^2.(1 + 0,75∙0,28)=991,23 тыс. руб.

4. Долговое обязательство на выплату 2 млн. руб. учтено за 2 года до срока. Определить полученную сумму, если производилось: а) полугодовое; б) поквартальное; в) помесячное дисконтирование по сложной учетной ставке 20 % годовых.

Решение:

Используя следующую формулу, определим полученную сумму, если производилось дисконтирование:



где F - наращенная сумма;

P - вложенная сумма;

n - количество лет;

d - сложная учетная ставка;

m - количество начислений процентов в году;

а) полугодовое:



б) поквартальное:



в) помесячное:



5. Банком выдан кредит на 9 месяцев под 24% годовых с ежеквартальным начислением сложных процентов. Определите величину простой учетной ставки, обеспечивающей такую же величину начисленных процентов. 
Решение:

Эквивалентность номинальной ставки сложных процентов при начислении процентов m раз в год и простой учетной ставки: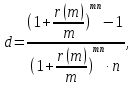



где r(m) – сложная процентная ставка; 

n - продолжительность финансовой операции в годах.

m- число начислений в году;

d – простая учетная ставка.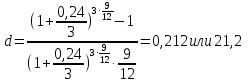



Т.е. величина простой учетной ставки, обеспечивающей такую же величину начисленных процентов, как и при ежеквартальном начислении сложных процентов при 24% годовых, составляет 21,2%.

6. Принято решение объединить три платежа стоимостью 10 000 долл., 20 000 долл. и 15 000 долл., срок уплаты которых наступит соответственно через 135, 166 и 227 дней от настоящего момента времени, в один платеж, равный им по сумме. Определить срок консолидированного платежа при использовании простой процентной ставки 8 % годовых. 
Решение:

1) Сумма консолидированного платежа согласно условию задачи: 

S₀=10+20+15=45 тыс. долл.

2) Срок выплаты консолидированного платежа найдем по формуле:



где i – ставка процента

S₀ – сумма консолидированного платежа;

P₀ – современная величина консолидируемых платежей.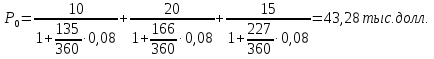







7. На вклад в 900 тыс. руб. каждые полгода начисляются сложные проценты по номинальной годовой процентной ставке 8 %. Оцените сумму вклада через 1,5 года с точки зрения покупательной способности, если ожидаемый темп инфляции –0,5 % за квартал. 
Решение:

1) Определим годовой темп инфляции:

I_p=(1+0,05)⁴=1,2155

2) Будущая стоимость вклада через 1,5 года составит:





3) Величина вклада с точки зрения ее покупательной способности равна: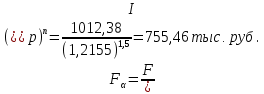



8. В банк на депозит внесено 100тыс руб..срок депозита-три года. Сложная ссудная ставка равна 8% годовых. Определить ставку налога на начисленные проценты, если после его уплаты у вкладчика осталось 120 ты. Руб

9. В начале каждого года Вы вкладываете 500 тыс. руб.в банк, ежегодно начисляющий сложные проценты по ставке 9% годовых. Определить сумму, которая накопится на счете через 5 лет. Если эта сумма получается в результате однократного помещения денег в банк, то какой величины должен быть внос?

10 Какую сумму необходимо положить в банк, чтобы в течение 8 лет иметь возможность снимать со счета по 3000 в конце каждого полугодия и за 8 лет исчерпать счет полностью, если банк ежеквартально начисляет сложные проценты по ставке 10% годовых?

11предприниматель планирует накопить1 млн руб осуществляя в начале года равные вклады в банк под сложную ссудную ставку 10%. Какой величины должен быть каждый вклад, чтобы накопить необходимую сумму за 5 лет,за 10 лет?

12. Некоторая фирма создала фонд в размере5млн руб для премирования своих работников. Фирма предполагает ежегодно выплачивать работникам 600тыс.руб Найти срок использования фонда, если банк начисляет ежегодно сложные проценты по ставке 8% годовых?

13. Ежегодно в конце года на депозит вносится 100тыс.руб.Какая сумма накопится на депозите через 5 лет,если банк ежегодно начисляет сложные процеты по учетной ставке 10% годовых, Как изменится ответ, если банк будет начислять проценты по сложной ссудной ставке10% годовых.

14.найти годовую ренту- сумму сроком в 10 лет для двух годовых рент: одна продолжается 5 лет с годовым платежом 1 млн руб., другая – продолжительность 8 лет с годовым платежом 0,8 млн руб. Годовая ставка сдложных процентов равна 8%.

15. Согласно условиям финансового контракта на счет вбанке в течение 5 летбудут поступать в начале года денежные суммы,первая из которых равна 60тыс. Руб, а каждая следующая будет увеличиваться на 3 тыс.руб. Оцените этот аннуитет,если банк применяет процентную ставку12%годовых и сложные проценты начисляются в начале года.

16. Финансовая компания в течение трех лет в соотвествии со своими обязательствами должна выплачивать вкладчикам 8млн руб ежегодно. Какой суммой должна располагать компания,чтобы иметь возможность выполнить обязательства, если норма доходности составляет 12% за год и выплаты происходят постоянно и достаточно непрерывно.