Промежуточная контрольная работа 7 класс,с КЭСами. промежуточная контрольная работа с кэс 7 класс. Решение всех заданий. Время, отводимое на выполнение работы 40 минут Темы, подлежащие контролю
 Скачать 51.34 Kb. Скачать 51.34 Kb.
|
|
Пояснительная записка Цель работы: контроль знаний, умений и навыков учащихся 7 класса, полученных при изучении математических выражений, тождеств, уравнений, функций и степеней с натуральным показателем. Форма работы: письменная контрольная работа, содержащая полное решение всех заданий. Время, отводимое на выполнение работы: 40 минут Темы, подлежащие контролю: Выражения. Преобразование выражений. Уравнения с одной переменной. Функции. Степень и её свойства Статистические характеристики Описание работы: Контрольная работа содержит 2 варианта по 6 заданий в каждом. Составлены с учетом УМК по алгебре 7 класса автора Ю. Н. Макарычев, Н. Г. Миндюк, 2017 год. Первое задание проверяет знание свойств степени с натуральным показателем. Второе задание проверяет умение правильно преобразовывать выражение, используя правило раскрытия скобок, а также приведение подобных слагаемых и умение находить значение буквенного выражения. Третье задание проверяет умение решать простейшие задачи на составления уравнений. Четвертое задание проверяет умение решать уравнения, используя правила преобразования выражений. Пятое задание проверяет навыки построения графика линейной функции. Шестое задание проверяет не только нахождения статистических характеристик, но и умение правильно находить значение буквенного выражения при заданных значениях переменных. Решение контрольной работы должно содержать подробное объяснение по каждому заданию. Критерии оценивания Первое задание оценивается в 2 балла 1балл - верное применение свойств степени 1 балл – нет вычислительных ошибок. Второе задание оценивается в 2 балла 1 балл – правильное применение свойств раскрытия скобок и приведение подобных слагаемых 1 балл - нет вычислительных ошибок. Третье задание оценивается в 2 балла 1балл – правильно описан процесс в задаче и по этому описанию составлено уравнение 1 балл - нет вычислительных ошибок. Четвертое задание оценивается в 2 балла 1 балл - правильное применение свойств раскрытия скобок и приведение подобных слагаемых 1 балл - нет вычислительных ошибок. Пятое задание оценивается в 3 балла 1 балл – определен вид функции и что является ее графиком, правильно взято количество точек и они верно вычислены по формуле. 1 балл – график линейной функции правильно построен в системе координат. 1 балл – правильно найдены точки пересечения с осями координат Шестое задание оценивается в 3 балла 1 балл - правильно найдены значения функции по формуле 1 балл – ряд чисел упорядочен и нет вычислительных ошибок 1 балл – правильно найдены все статистические характеристики. Максимальное количество баллов за контрольную работу 14 баллов Отметка «5» выставляется, если выполнены задания на 13 – 14 баллов. Отметка «4» выставляется, если выполнены задания на 9 – 12 баллов. Отметка «3» выставляется, если выполнены задания на 6 – 8 баллов. Отметка «2» выставляется, если выполнены задания на сумму менее 6 баллов.
Промежуточная контрольная работа по алгебре 7 класс Вариант 1 1. Выполните действия: а) х5 х9; б) х10 : х3; в) (х2)7; г) (2х5)3. 2. Упростите выражение: 7а – 2(3а - 1), если а = 1,5. 3. Мастер изготовил в 2 раза больше деталей, чем его ученик. Сколько деталей изготовил каждый из них, если вместе они изготовили 42 детали? 4. Решите уравнения: а) (7х +1) – (6х+3) = 5; б) 4х-12= 3(х-1) 5. Постройте график функции: у = 4х – 3. Найдите точки пересечения графика с осями координат. 6. Дана функция у = 3х2 – 5 составьте таблицу значений функции в точках -2;-1; 0; 1;2; 3;4 и для полученного ряда чисел найдите: а) среднее арифметическое; б) размах; в) моду; г) медиану. Промежуточная контрольная работа по алгебре 7 класс Вариант 2 1. Выполните действия: а) а9 а10; б) а14 : а6; в) (а5)4; г) (3а3)4. 2. Упростите выражение: 13а – 4(3а – 1), если а = 2,5. 3. Турист проехал на велосипеде в 5 раз большее расстояние, чем прошёл пешком. Весь путь туриста составил 30 км. Какое расстояние турист проехал? 4. Решите уравнения: а) (6х +1) – (3 – 2х) = 14; б) 4(х-1)= 2(х+2) 5. Постройте график функции: у =4 - 3х. Найдите точки пересечения графика с осями координат. 6. Дана функция у =2х - х2 составьте таблицу значений функции в точках -1; 0; 1;2; 3;4;5 и для полученного ряда чисел найдите: а) среднее арифметическое; б) размах; в) моду; г) медиану. Решение к контрольной работе Вариант 1 1. Выполните действия: а) х5 х9 = х14; б) х10 : х3= х7; в) (х2)7= х14; г) (2х5)3=8х15. 2. Упростите выражение 7а – 2(3а - 1) и найдите его значение при а = 1,5. 7а – 6а +2 = а + 2. Если а = 1,5, то а+2 = 1,5 + 2 = 3,5. 3. Мастер изготовил в 2 раза больше деталей, чем его ученик. Сколько деталей изготовил каждый из них, если вместе они изготовили 42 детали? Пусть х деталей изготовил ученик, тогда 2 х деталей изготовил рабочий. А по условию задачи вместе они изготовили 42 детали. Составим и решим уравнение. 2х + х = 42, 3х = 42, х = 42:3, х = 14. Значит 14 деталей изготовил ученик, тогда мастер изготовил 2 * 14 = 28 деталей. Ответ:14 деталей, 28 деталей. 4. Решите уравнение: а) (7х +1) – (6х+3) = 5 7х +1 – 6х – 3 = 5, х -2 = 5, х = 7. Ответ 7. б) 4х – 12 = 3(х – 1) 4х – 12 = 3х – 3 4х – 3х = -3 + 12 х = 9 Ответ: 9 5. Постройте график функции: у = 4х – 3. Найдите точки пересечения графика с осями координат. у = 4х – 3 это линейная функция, график прямая, для построения достаточно двух точек
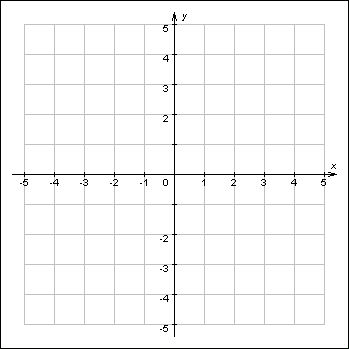 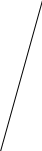 С осью 0у (0,-3), с осью ох (0,7;0) 6. Дана функция у = 3х2 – 5 составьте таблицу значений функции в точках -2;-1; 0; 1;2; 3;4 и для полученного ряда чисел найдите: а) среднее арифметическое; б) размах; в) моду; г) медиану.
-5, -2, -2, 7, 7, 22, 43 Среднее арифметическое: 10 Размах: 43 – (-5) = 48 Мода: 7, - 2. Медиана: 7. Вариант 2 1. Выполните действия: а) а9 а10=а19; б) а14 : а6= а8; в) (а5)4= а20 г) (3а3)4= 81а12 2. Упростите выражение 13а – 4(3а - 1) и найдите его значение при а = 2,5. 13а – 12а + 4 = а + 4. Если а = 2,5, то а + 4 = 2,5 + 4 = 6,5 3.Турист проехал на велосипеде в 5 раз большее расстояние, чем прошёл пешком. Весь путь туриста составил 30 км. Какое расстояние турист проехал на велосипеде? Пусть х км турист прошел пешком, тогда 5х км турист проехал на велосипеде. А по условию задачи весь путь туриста составил 30 км. Составим и решим уравнение. 5х + х = 30, 6х = 30, х = 30:6, х= 5. Значит 5 км турист прошел пешком, тогда на велосипеде он проехал 5 *5 = 25 км. Ответ: 25 км. 4. Решить уравнение: а) (6х+1) –(3 – 2х) = 14 6х + 1 – 3 +2х = 14 6х + 2х = 14 – 1 + 3 8х = 16 х = 16 : 2 х = 8. Ответ: 8 б) 4(х – 1) = 2(х + 2) 4х – 4 = 2х + 4 4х – 2х = 4 + 4 2х = 8 х = 8 : 2 х = 4 Ответ: 4 5. Постройте график функции: у =4 - 3х. Найдите точки пересечения графика с осями координат. у =6 - 3х – это линейная функция, график прямая, для построения достаточно двух точек
 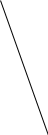 С осью оу (0,4), с осью ох (1,3; 0) 6. Дана функция у =2х - х2 составьте таблицу значений функции в точках -1; 0; 1;2; 3;4;5 и для полученного ряда чисел найдите: а) среднее арифметическое; б) размах; в) моду; г) медиану.
-15, -8 ,-3, -3, 0, 0, 1 Среднее арифметическое: -4 Размах: 1 – (-15) = 16 Мода: 0, - 3. Медиана: - 3. |
