Решение
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Задание №1. Найти матрицу D=AB-BA+A-1+BT, где Вт получается из В её транспонированием. 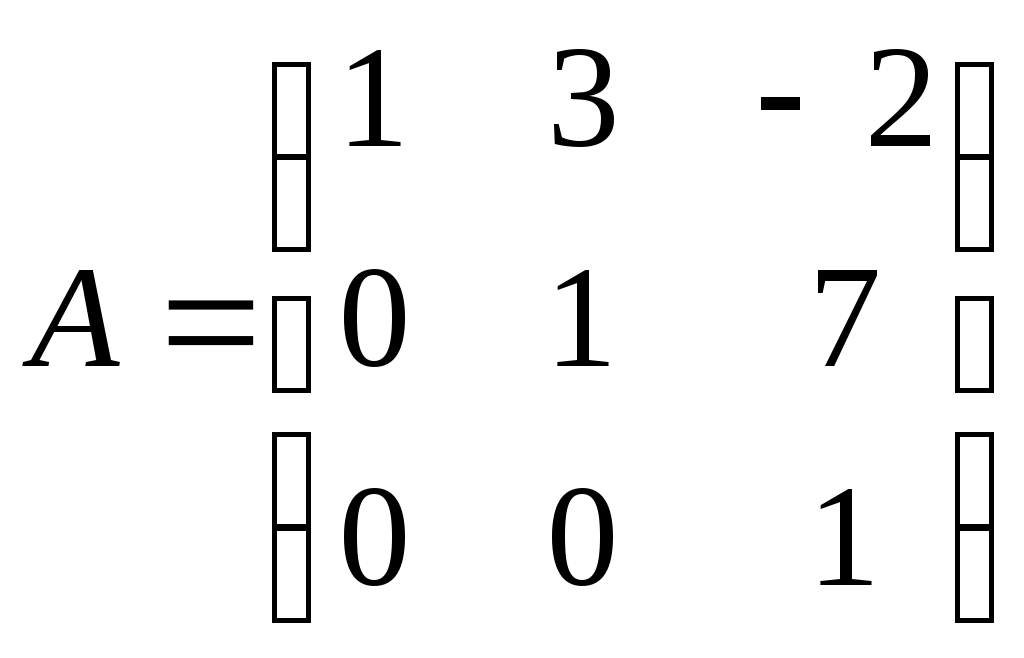 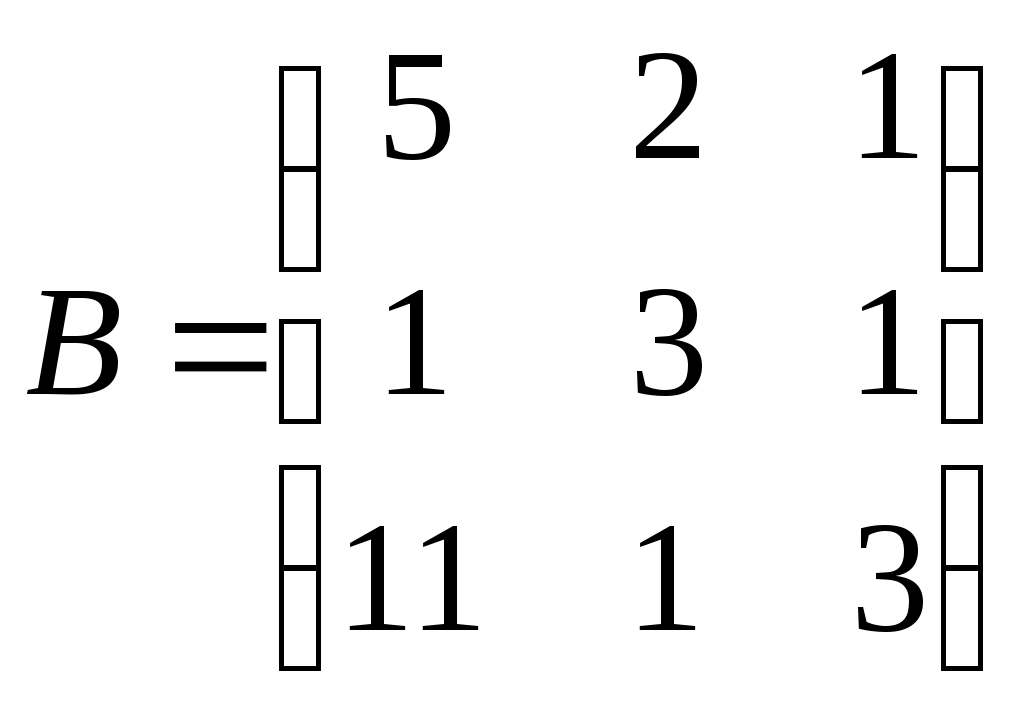 Решение: 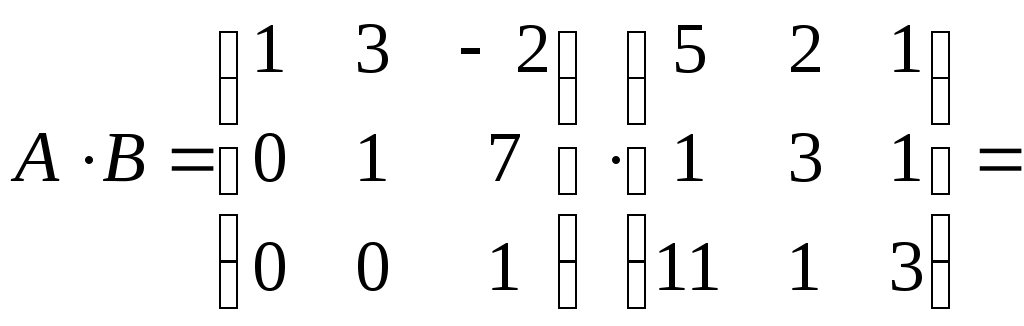 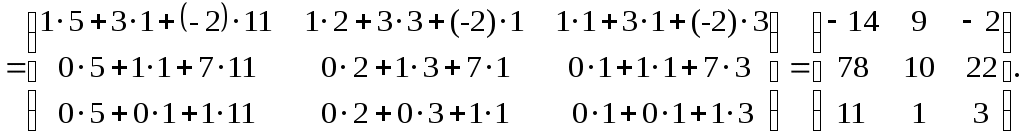 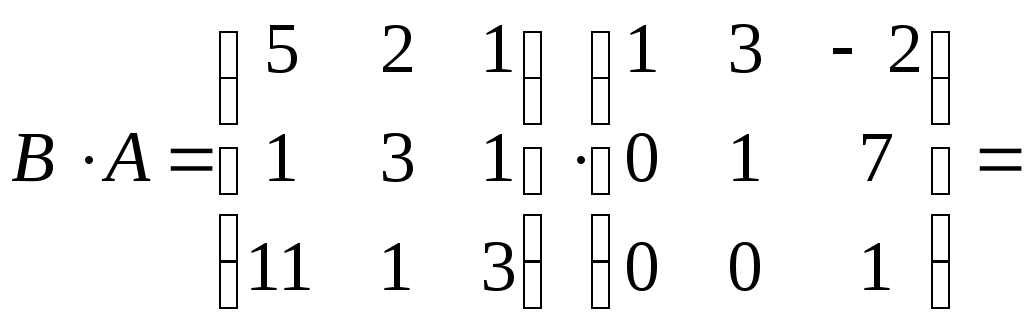 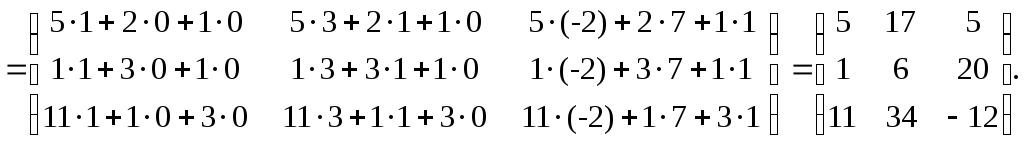 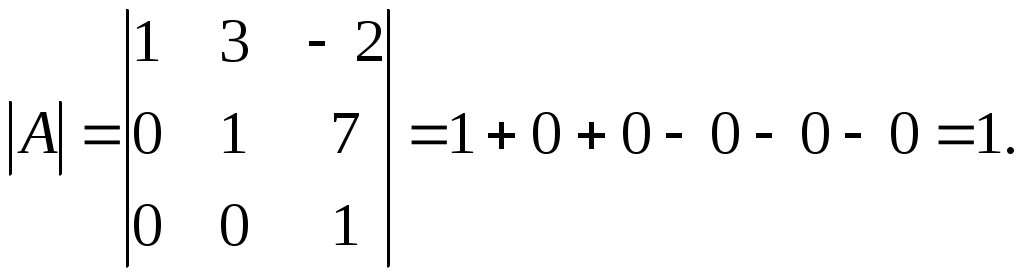 Так как определитель матрицы не равен нулю, следовательно, матрица не вырожденная и существует обратная матрица, которая вычисляется по формуле: 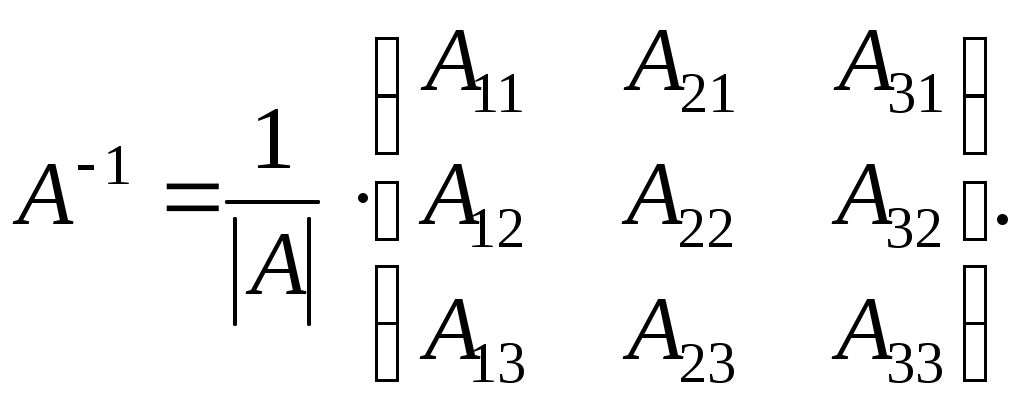 Вычислим алгебраические дополнения. Следовательно, обратная матрица имеет вид 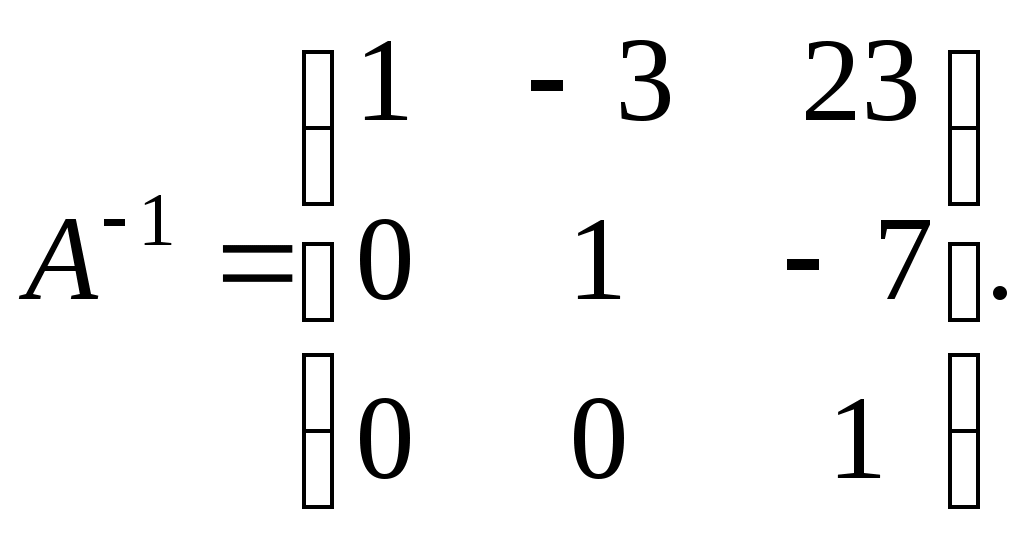 Транспонируем матрицу В, для этого запишем строки данной матрицы в виде столбцов с теми же самыми номерами 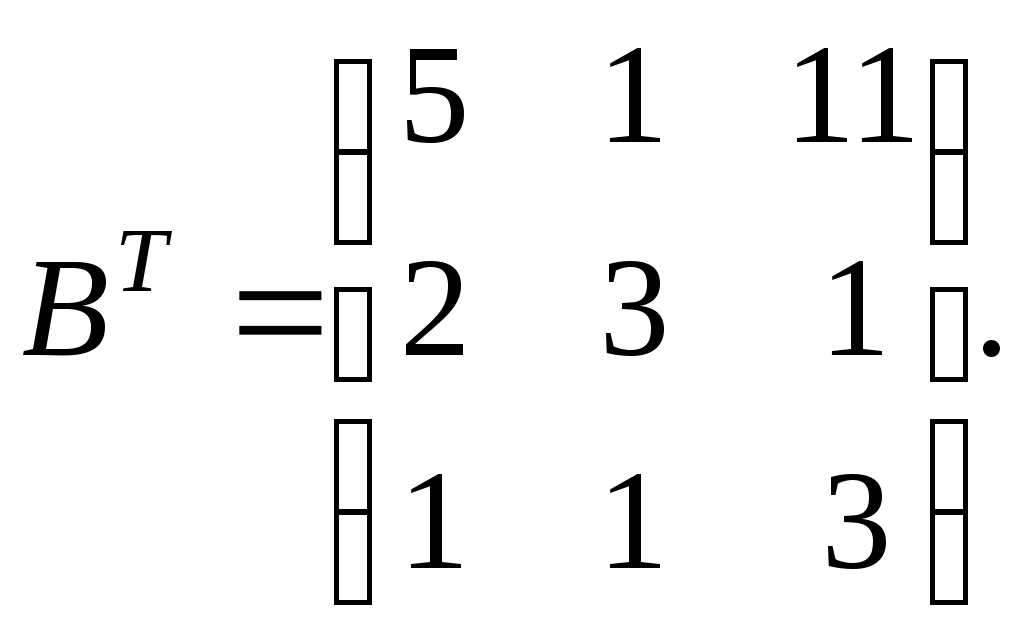 Вычислим матрицу D=AB-BA+A-1+BT 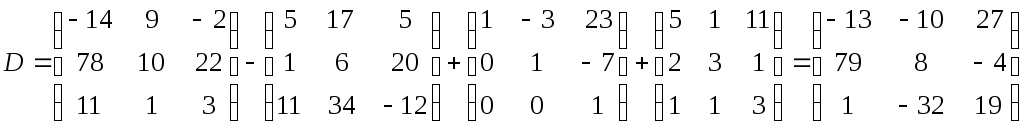 Ответ: 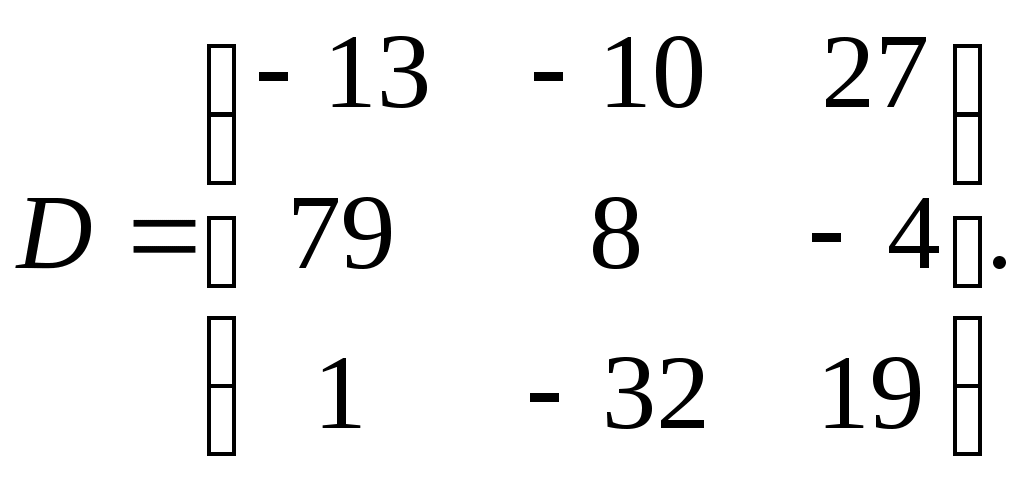 Задание №2. Выяснив вопрос о совместности системы линейных уравнений с помощью теоремы Кронекера-Капелли, решить методом последовательного исключения неизвестных. 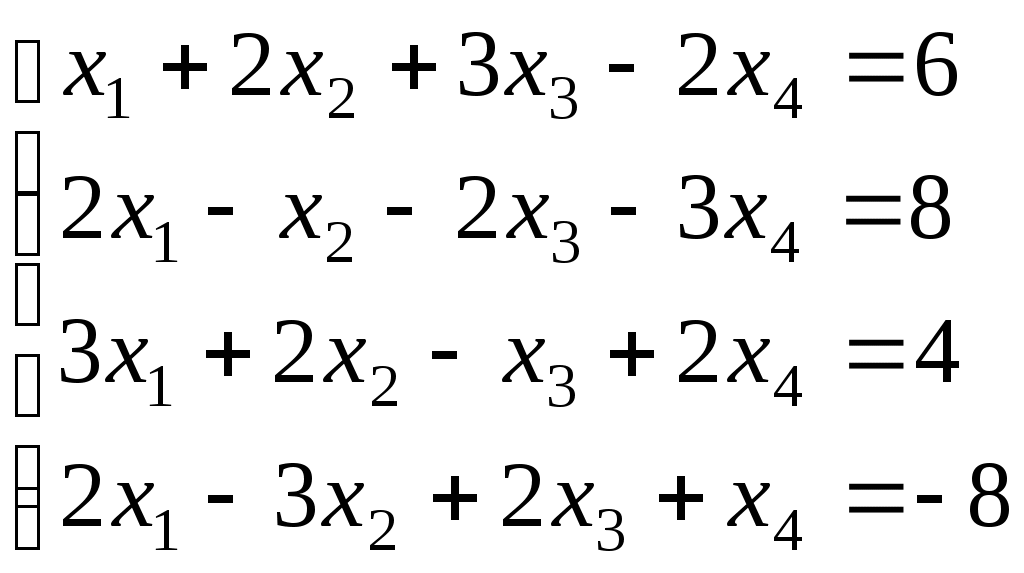 Решение: Запишем коэффициенты СЛАУ в виде расширенной матрицы и приведем данную матрицу к ступенчатому виду: 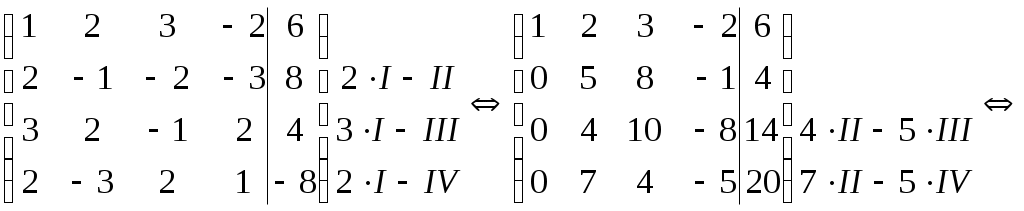 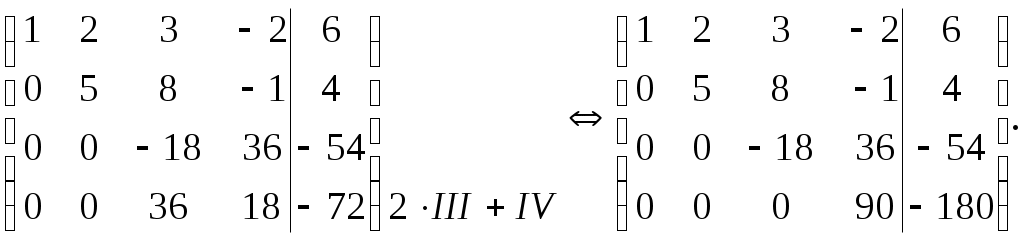 Ранг основной матрицы Ответ: система совместна. Задание №3. Решить систему уравнений по правилу Крамера, с помощью обратной матрицы, методом Жордана-Гаусса 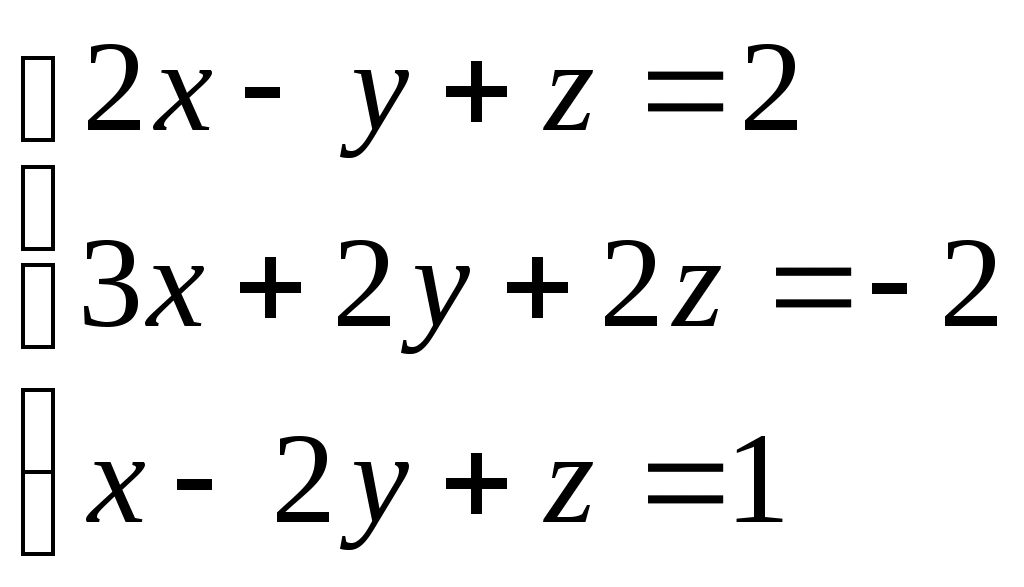 Решение: Запишем коэффициенты левой части системы уравнений в виде определителя 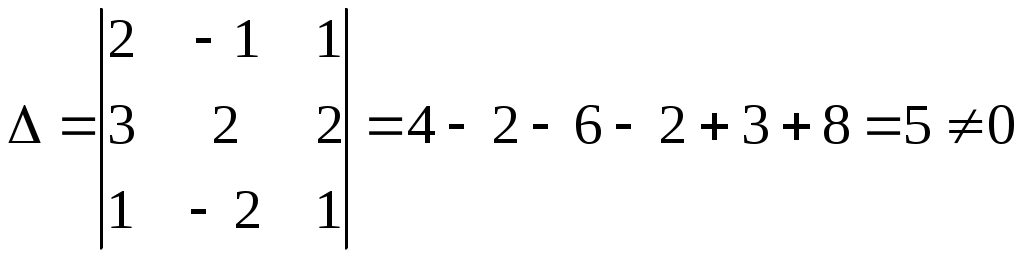 Определители 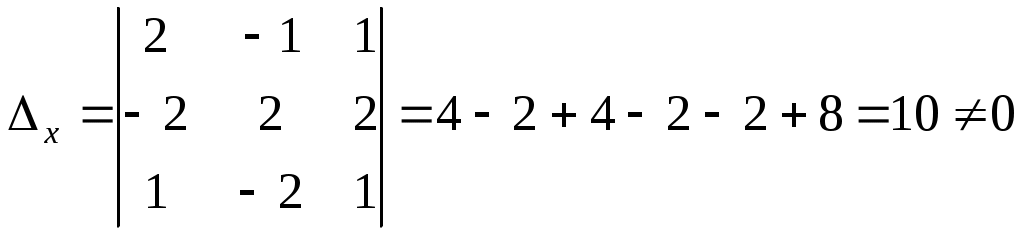 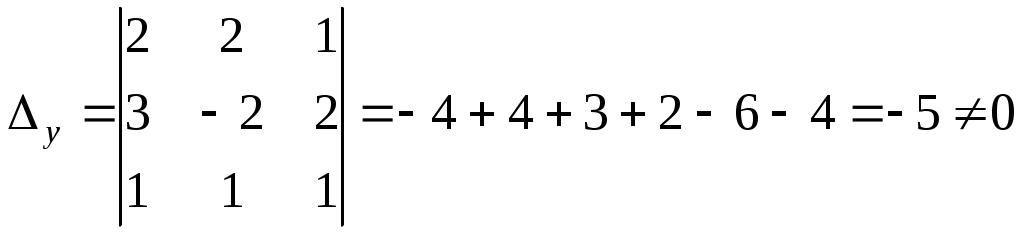 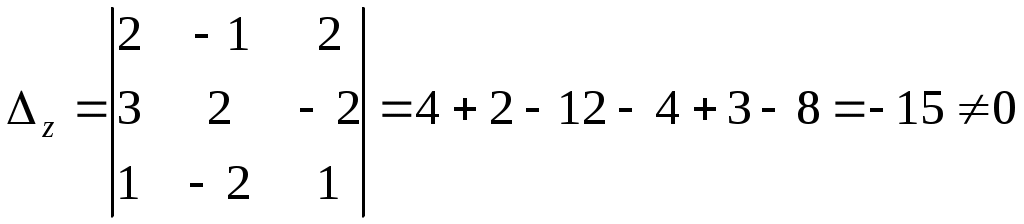 Ответ: Задание №4. SABC тетраэдрS(1,4,2), А(-3,2,3), В(3,0,6), С(4,2,5). Средствами аналитической геометрии найти: а). б). в). VSABC; г). Площадь д). Высоту из вершины S; е). Уравнение плоскости SAB; ж). Уравнение прямой, проходящей через точку А, параллельно прямой SC; з). Уравнение плоскости, проходящей через точку А перпендикулярно SA; и). Доказать, что вектора Решение: а). 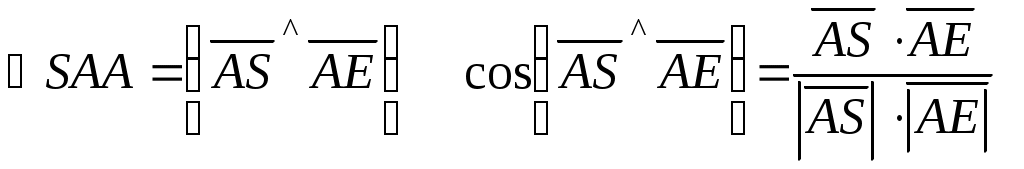 по определению скалярного произведения двух векторов. по определению скалярного произведения двух векторов.Найдем координаты векторов Тогда 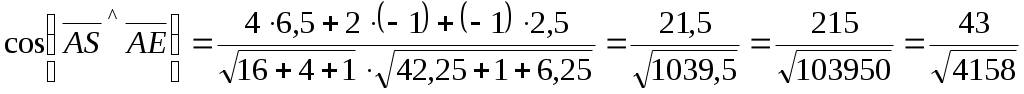 б). Проекция вектора в). Объем тетраэдра вычисляется по формуле: 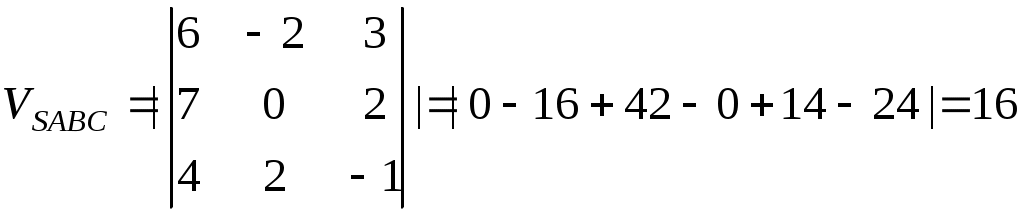 Ответ: г). Площадь треугольника 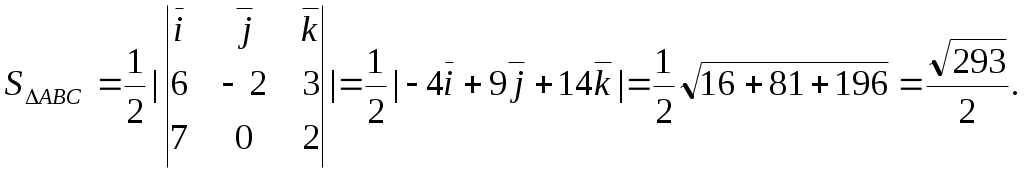 Ответ: д). Высоту тетраэдра выразим из формулы объема тетраэдра Ответ: е). Запишем уравнение плоскости SAB как уравнение плоскости, проходящей через три точки S, A и B, оно имеет вид: 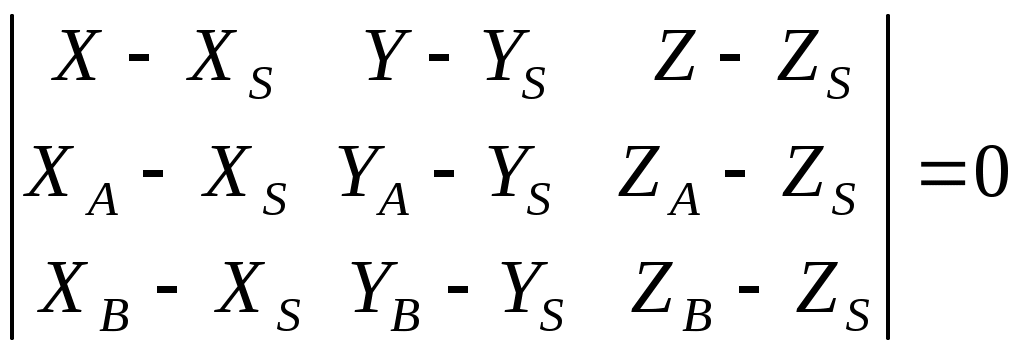 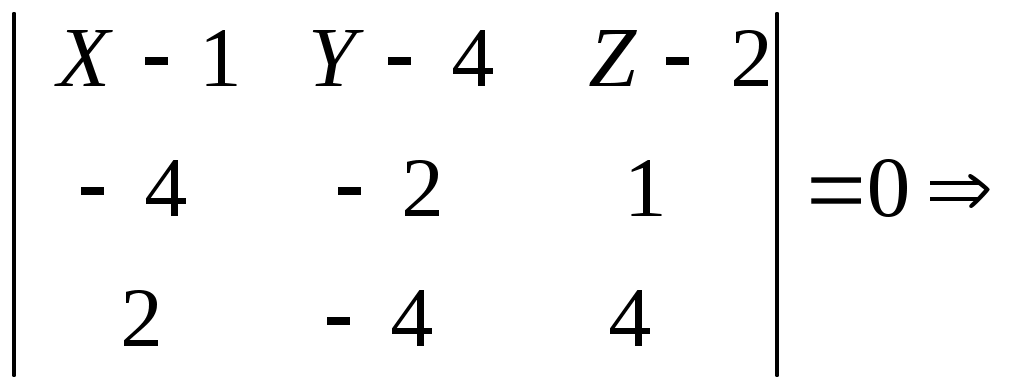 ж). Запишем уравнение прямой Две прямые параллельны, если координаты их направляющих векторов пропорциональны, то есть з). Уравнение плоскости, проходящей через точку A и В данном случае за вектор и). Используем признак линейной независимости векторов, вычислим определитель, составленный из координат векторов 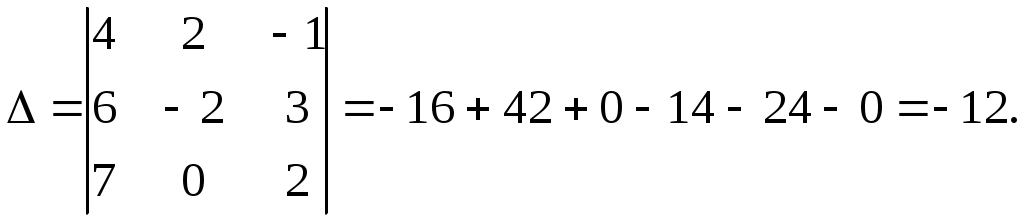 Определитель Найдем координаты вектора Тогда координаты точки В итоге координаты вектора Разложим вектор Запишем данное разложение в координатной форме и получим систему уравнений: 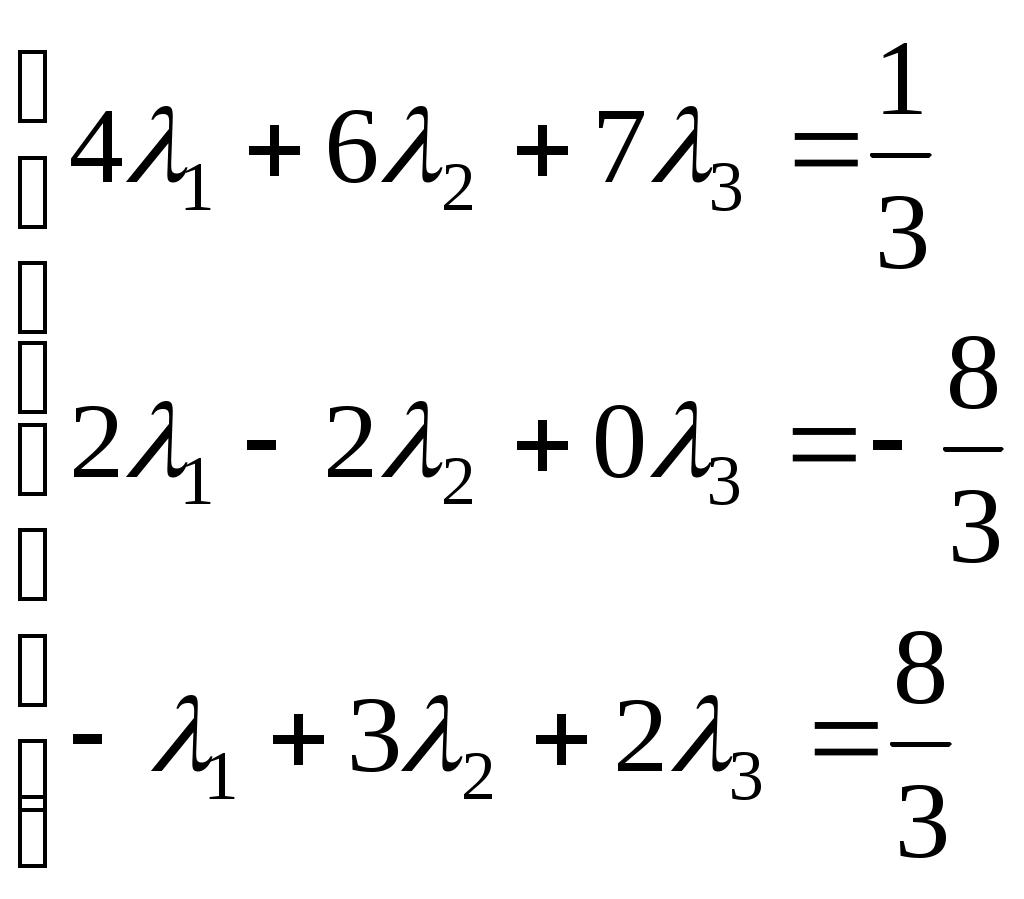 Решим систему с помощью обратной матрицы. Запишем данную систему в матричном виде 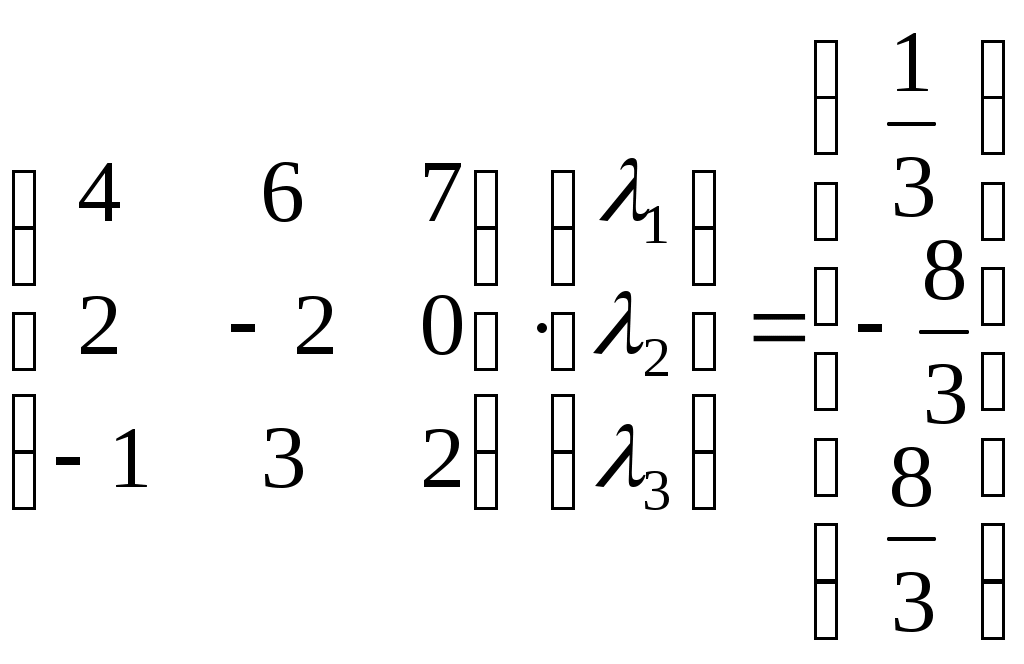 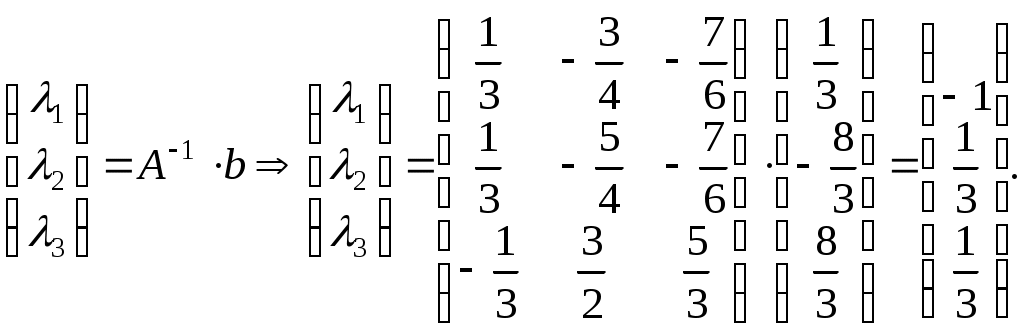 Задание №5. Найти указанные пределы функций, не пользуясь правилом Лопиталя. а). б). в). г). Решение: Используя определение и свойства предела функций, получим а1). 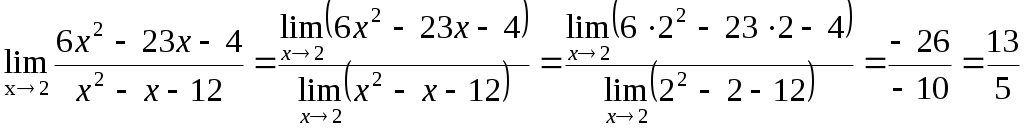 а2). а3). 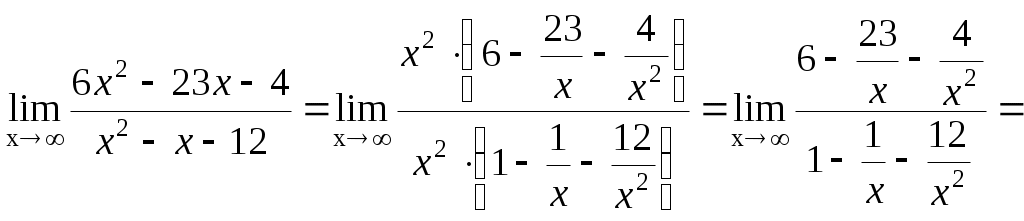  б). введем новую переменную Логарифмируя это равенство по основанию   в). воспользуемся формулой второго замечательного предела г). Умножим и разделим выражение  Задание №6. Найти производные функций а). б). в). г). Применяя дифференциал к приближенным вычислениям, найдите приближенное значение приращения функции Решение: а). Воспользуемся формулой производной частного  б). Воспользуемся формулой производной показательной функции в). Данная функция, заданная неявно, найдем производную от обеих частей равенства, учитывая, что   г). Приращение функции равно произведению производной функции и приращения аргумента Подставляем значения Ответ: Задание №7. Исследовать функцию Схема исследования: 1. Найти область определения. 2. Исследовать на четность, нечетность, периодичность. 3. Найти точки пересечения графика функции с осями координат. 4. Исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в точках разрыва. 5. Найти точки экстремума функции и интервалы ее монотонности. 6. Найти точки перегиба, интервалы выпуклости и вогнутости графика функции. 7. Найти асимптоты графика функции. Решение: Функция определена на всей числовой прямой, то есть Найдем точки пересечения графика функции с осью График функции не имеет точек разрыва. Найдем производную:  приравниваем производную к нулю и находим критические точки Найдем промежутки возрастания и убывания функции 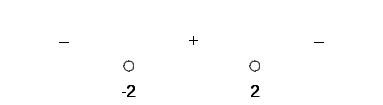 В промежутке функции в этом промежутке положительная, а в промежутках найдем вторую производную: 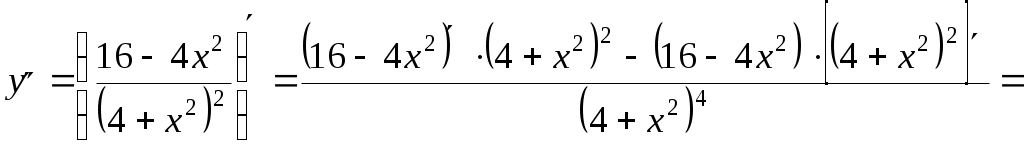 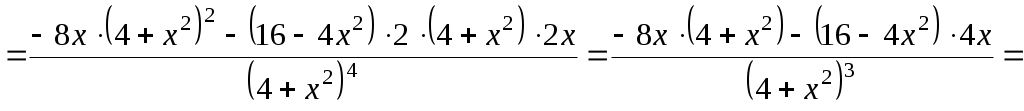 Приравниваем производную к нулю и находим точки перегиба 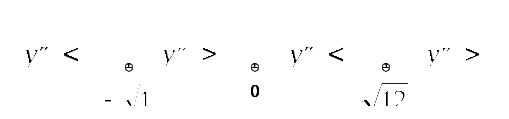 В промежутках В промежутках При переходе через точки Невертикальные асимптоты графика ищем в виде 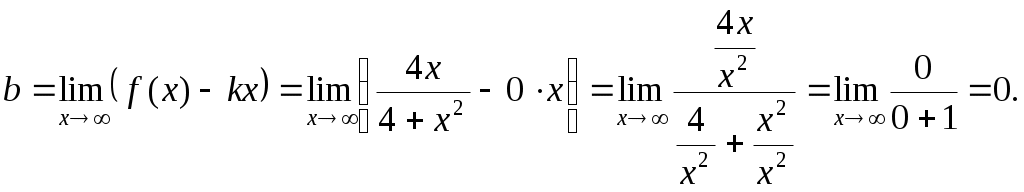 Отсюда имеем горизонтальную асимптоту Используя полученные данные, построим искомый график. 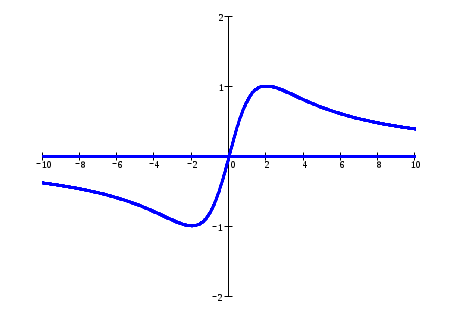 |
