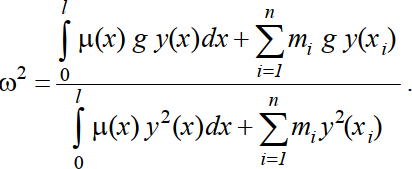СРО-12. Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4

• Название: Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4
• Дата: 10.04.2022
• Размер: 0.6 Mb.
• Имя файла: СРО-12.doc
• Тип: Решение; #459042
• страница: 4 из 5

Применение энергетических методов в динамических расчетах зданий и сооружений.

1. Метод Релея

При собственных колебаниях консервативных систем (систем без потери энергии) вы- полняется принцип сохранения энергии - энергия свободно колеблющейся системы остается постоянной, если не развиваются диссипативные силы. На этой основе разработан энергети- ческий метод, позволяющий определять низшую частоту и форму собственных колебаний ди- намической системы. В нем принимается, что в колебательной системе происходит полный переход кинетической энергии в потенциальную энергию и наоборот, и поэтому выполняется условие

(3.103)

В качестве примера рассмотрим собственные колебания системы, показанной на рис.

1.2 а. При соответствующем выборе начала отсчета времени перемещение и скорость массы

m(рис. 1.2 б) определяются как

Потенциальная энергия системы полностью определяется энергией упругой деформа- ции пружины жесткости r:

(3.104)

а кинетическая энергия массы

(3.105)

Для момента времени t=T/4[по формуле (1.5) t=π/2ω] имеем, что кинетическая энер- гия (3.105) равна нулю, а потенциальная энергия (3.104) достигает максимальной величины

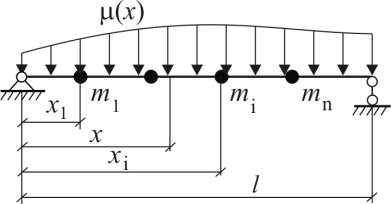
Аналогично, для t = T/2 = π/ω потенциальная энергия (3.104) равна нулю, а кинетиче- ская энергия (3.105) достигает максимума



Тогда по условию (3.103) получаем ω² = r∕т, что совпадает с формулой круговой ча- стоты (2.15) для любой системы с одной степенью свободы. Однако теперь оно выведено с применением метода Релея.

Теперь рассмотрим балку с погонной массой μ(χ) и n сосредоточенными массами m₁, m₂, ..., m_n (рис. 3.22).

Рис. 3.22

(3.106)

Пусть эта балка совершает колебания по основной форме Тогда скорость колебаний будет
С их помощью можно вычислить максимальные значения кинетической и потенциаль- ной энергий К_max и U_max: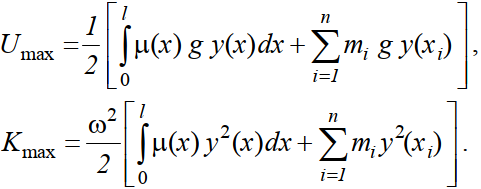



Учитывая (3.103), приравняем эти два выражения. Тогда получим

(3.108)

Это выражение называется формулойРелея.

Так как функция y(x) заранее неизвестна, то приходится задаваться некоторой прибли- женной функцией, отличной от истинной. Поэтому формула (3.108) дает приближенное зна- чение частоты. Можно доказать [6], что вычисленное по формуле Релея значение частоты соб- ственных колебаний отличается от точного с некоторым избытком. Подбирая подходящие функции, аппроксимирующие изогнутую ось балки при колебаниях, можно вычислить соот- ветствующие значения собственных частот. Наименьшее из них будет давать наилучшее при- ближение к истинному значению частоты.

Итак, формула Донкерлея дает приближенное значение частоты «снизу», формула Релея - приближение «сверху». Одновременное применение этих формул позволяет устано- вить границы, в пределах которых находится истинное значение основной частоты колебаний.