СРО-12. Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4

• Название: Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4
• Дата: 10.04.2022
• Размер: 0.6 Mb.
• Имя файла: СРО-12.doc
• Тип: Решение; #459042
• страница: 5 из 5

Метод Релея-Ритца

Метод Релея получил дальнейшее обобщение как метод Релея-Ритца. В нем условие (3.107) используется для определения нескольких низших частот и форм собственных колеба- ний системы. При этом общее решение уравнения собственных колебаний приближенно пред- ставляется как сумма сокращенного ряда

(3.109)

где учитываются sпервых форм собственных колебаний.

Запишем его в матричном виде y = az, где

^{- матрица из sформ собственных колебаний системы, z = {z}1^z2 ^{… zs} - сокращенный вектор} нормальных координат.

По аналогии с (3.104) и (3.105), потенциальная и кинетическая энергии системы со мно- гими степенями свободы определяются так:

	(3.110)
	(3.111)

где r - матрица жесткости, m - матрица масс.

С учетом того, что при собственных колебаниях y = a sin (ωt + φ) (см. формулу 3.8) и что y = az , имеем


Приравнивая их, получаем формулу

(3.112)

Если известны нормальные координаты z, то эта формула должна давать минимальные значения частот собственных колебаний. Чтобы этого добиться, данное уравнение рассматри- вается как функционал от многих переменных и исследуется на экстремум. Для этого берутся частные производные по каждой из z_iи все они приравниваются нулю. Тогда получается си- стема однородных уравнений относительно z:

(3.113)

Если обозначить r* = a^tra и m*= a^tma, получим уравнение из которого определяются низшие частоты ω_iи z_i.

Тогда по формуле y = az определяются низшие формы собственных колебаний исход- ной системы со многими степенями свободы.

3. Метод постоянного ускорения

Для решения задач динамики сооружений разработаны специальные методы решения дифференциальных уравнений. Одним из таких является метод постоянного ускорения. Этот метод позволяет определять поведение динамической системы поэтапно, через определенные интервалы.

Рассмотрим динамическую систему с демпфированием. Уравнение вынужденных ко- лебаний такой системы имеет вид

(3.114)

где m - матрица масс, c - матрица демпфирования, r - матрица жесткости, y=y(t) - вектор пе- ремещений, P=P(t) - вектор нагрузки.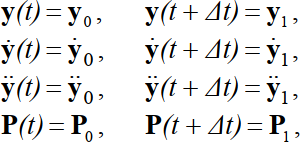

Если в интервале от t до t+Δtизвестны величины

то для них уравнение (3.108) запишется как

	(3.115)
	(3.116)

Для пошагового расчета в методе постоянного ускорения используется гипотеза: в каждый интервал времени (т. е. при 0<τ<Δt) ускорение постоянно и равно среднему ускоре- нию:

(3.117)

С другой стороны,

(3.118)

Поэтому (3.117) можно записать так:


Если проинтегрировать обе стороны этого выражения, получим

(3.119)

Так как для момента времени τ=0у̇⁽𝑡 + 𝜏⁾ = у̇⁽𝑡⁾ = 𝑦̇₀, то 𝐶₁ = 𝑦̇₀. Значит,

(3.120)

Интегрируя, как и выше, получаем формулу вычисления перемещения в момент вре- мени τ:

(3.121)

Из формул (3.120) и (3.121) определяются скорость и перемещение на границе интер-

вала

	(3.122)
	(3.123)

1

0
^{Далее выразим ускорение и скорость через у}1^{, у}0^{, у}

относительно у^̈ ₁:

и у . Для этого решим (3.123)

(3.124)

где

Если подставить его в (3.122), получим

(3.125)

Теперь подставим (3.124) и (3.125) в (3.116) и получим уравнение

(3.126)

	(3.127)
	(3.128)

Начальное ускорение определяется из (3.115):

(3.129)

Полученные формулы позволяют вести расчет на вынужденные колебания демпфиро- ванной системы шаговым методом. Для этого участок движения (временный промежуток, в котором ведется расчет) необходимо поделить на малые интервалы.

В начальный момент времени (в начале колебаний) должны быть известны вектора начального прогиба у₀ и начального ускорения 𝑦̇₀. Кроме того, должен быть известен закон изменения внешней нагрузки, то есть должны быть известны значения нагрузки в начале дви- жения P₀ и в начале каждого интервала P₁, P₂ и т. д.

Ускорение 𝑦̈₀ в начале движения определяется из (3.129). Используя его, по (3.126), (3.125) и (3.124) определяются значения y₁, 𝑦̇₁ и 𝑦̈₁ в конце интервала. А они, в свою очередь, являются начальными условиями для расчета колебаний во втором интервале. Используя те же уравнения (3.126), (3.125) и (3.124) расчет можно продолжать далее.

Чтобы метод давал хороший результат, интервалы вычислений должны быть малыми.
Список использованных литератур:
1. Энциклопедический словарь

2. Ресурсы сети Интернет

3. «Строительная механика. Динамика и устойчивость сооружений» - Смирнов А. Ф.

4. «Динамика и устойчивость сооружений» - Шакирзянов Р.А. Шакирзянов Ф. Р.

стр.