СРО-12. Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4

• Название: Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4
• Дата: 10.04.2022
• Размер: 0.6 Mb.
• Имя файла: СРО-12.doc
• Тип: Решение; #459042
• страница: 3 из 5

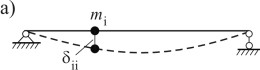
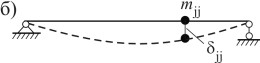
Формула Донкерлея

Вывод этой формулы основывается на приравнивании частот колебаний двух разных систем с одной степенью свободы.

Рассмотрим две балки одинаковой длины и жесткости, причем в первой балке сосредо- ^{точенная масса m}i ^{располагается в точке i, а во второй - масса m}j ^{располагается в точке j (рис.} 3.20).

Рис. 3.20

Частоты собственных колебаний этих балок будут

Из условия равенства этих частот следует Отсюда получаем

(3.100)

где η_ij=δjj∕δ_ii.Из формулы (3.100) вытекает, что если массу m_jиз точки jперенести в точку

iи умножить на коэффициент η_ij, то значение собственной частоты колебаний не изменится.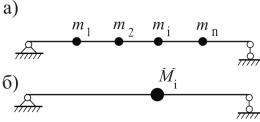

Теперь рассмотрим балку с nсосредоточенными массами (рис. 3.21 а).

Рис. 3.21

На основании предыдущих выкладок, все массы этой балки перенесем в некоторую точку i. Тогда, согласно (3.100), имеем



Умножая это уравнение на δ_iiи, учитывая (3.100), получаем

(3.101)

Но M_iδ_ii= 1∕ω², где ω - частота одномассовой системы с приведенной массой M_i

(рис. 3.21 б), а для любых 𝛿_𝑗𝑗 = ¹ ₂. Тогда (3.101) можно переписать в виде

⁄_𝜔𝑗

(3.102)

Эта формула называется формулой Донкерлея. Можно доказать [6], что основная ча- стота колебаний многомассовой системы, вычисленная по формуле Донкерлея, будет всегда меньше истинной частоты колебаний.