СРО-12. Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4

• Название: Решение задач динамики мкэ 2 2 Приближенные методы в динамике сооружений 4
• Дата: 10.04.2022
• Размер: 0.6 Mb.
• Имя файла: СРО-12.doc
• Тип: Решение; #459042
• страница: 2 из 5

Приближенные методы в динамике сооружений

Как установили в гл. 3, расчет колебательных систем можно вести по уравнениям ко- лебаний в формах метода перемещений и метода сил:

или

Очень часто при этом используется метод разложения по формам собственных колеба- ний, основанный на формуле (3.29):

^{где a}i^{-формы колебаний, z}i^{-нормальные координаты. Такой подход связан со сложной} задачей определения полного спектра частот и форм собственных колебаний системы со мно- гими динамическими степенями свободы из вековых уравнений высоких порядков

или

Однако во многих случаях определение всех частот и форм собственных колебаний из этих уравнений является из лишним, т. к. в практических расчетах часто используется лишь низший спектр собственных частот и соответствующие им формы колебаний.

При вычислении ограниченного числа частот и форм собственных колебаний широко применяются приближенные методы. Рассмотрим некоторые из них.

3. Метод приведенных масс

В предыдущей главе 3.7 мы убедились, что даже расчет такой простейшей балки как системы с распределенной массой приводит к дифференциальному уравнению, имеющему бесчисленное число решений. Если же динамическая система будет состоять из большого числа элементов, то ее расчет приведет к системе из множества дифференциальных уравнений в частных производных с многочисленными граничными условиями, решение которой стано- вится весьма сложной или даже неразрешимой задачей.

Упрощение решения достигается сосредоточением масс в дискретных точках. Такой метод называется методом приведенных масс. В нем величины приведенных масс находят из условия равенства кинетических энергий заданной и приведенной систем:

(3.99)

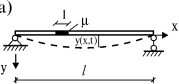
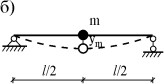
Как пример приведения массы распределенной системы к сосредоточенной массе рас- смотрим шарнирно-опертую балку с погонной массой μ(рис. 3.19 а).

	Рис. 3.19

Примем прогиб балки во время колебаний в виде произведения 2-х функций:

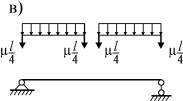
^{где y}0^{(x) - форма колебаний. Тогда кинетическая энергия участка балки длиной dxбудет}



где 𝑦̇ - скорость движения. Определим полную кинетическую энергию колеблющейся балки с распределенной массой: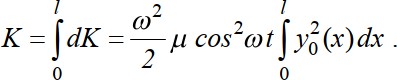


Если всю распределенную массу балки сосредоточить в виде некоторой приведенной массы mв середине балки (рис. 3.19 б), ее кинетическая энергия будет

^{Из условия равенства К = К}пр ^{получаем}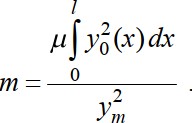



Для вычисления величины приведенной массы зададимся формой колебаний:

удовлетворяющей граничным условиям закрепления балки. Подставив ее в выражение массы, получаем

Так как податливость средней точки балки равна 𝛿 =

_𝑙3


48𝐸𝐼
, то по известной формуле

для частоты колебаний системы с одной степенью свободы (2.15) получаем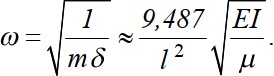



Если же взять форму колебаний в виде



получим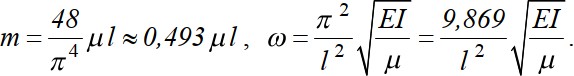



Этот результат можно считать “точным”, т. к. принятая форма колебаний совпадает с первой формой собственных колебаний стержня (формула 3.98 при n=1).

Если же принять приведенную массу как сумму реакций для двух половин балки, за- груженных распределенной массой μ(рис. 3.19 в), имеем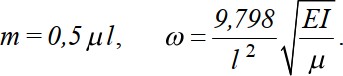



Получили решение достаточно близкое к точному. На основании этого, при использо- вании метода приведенных масс поступают так:

• 
  стержневую систему делят на участки;
  
• 
  массы участков делят пополам и сосредотачивают по их концам;
  
• 
  соседние массы объединяют.