Работа. Решение задач на аналитический расчёт режима покоя транзисторных каскадов с общим эмиттером
 Скачать 227.5 Kb. Скачать 227.5 Kb.
|
|
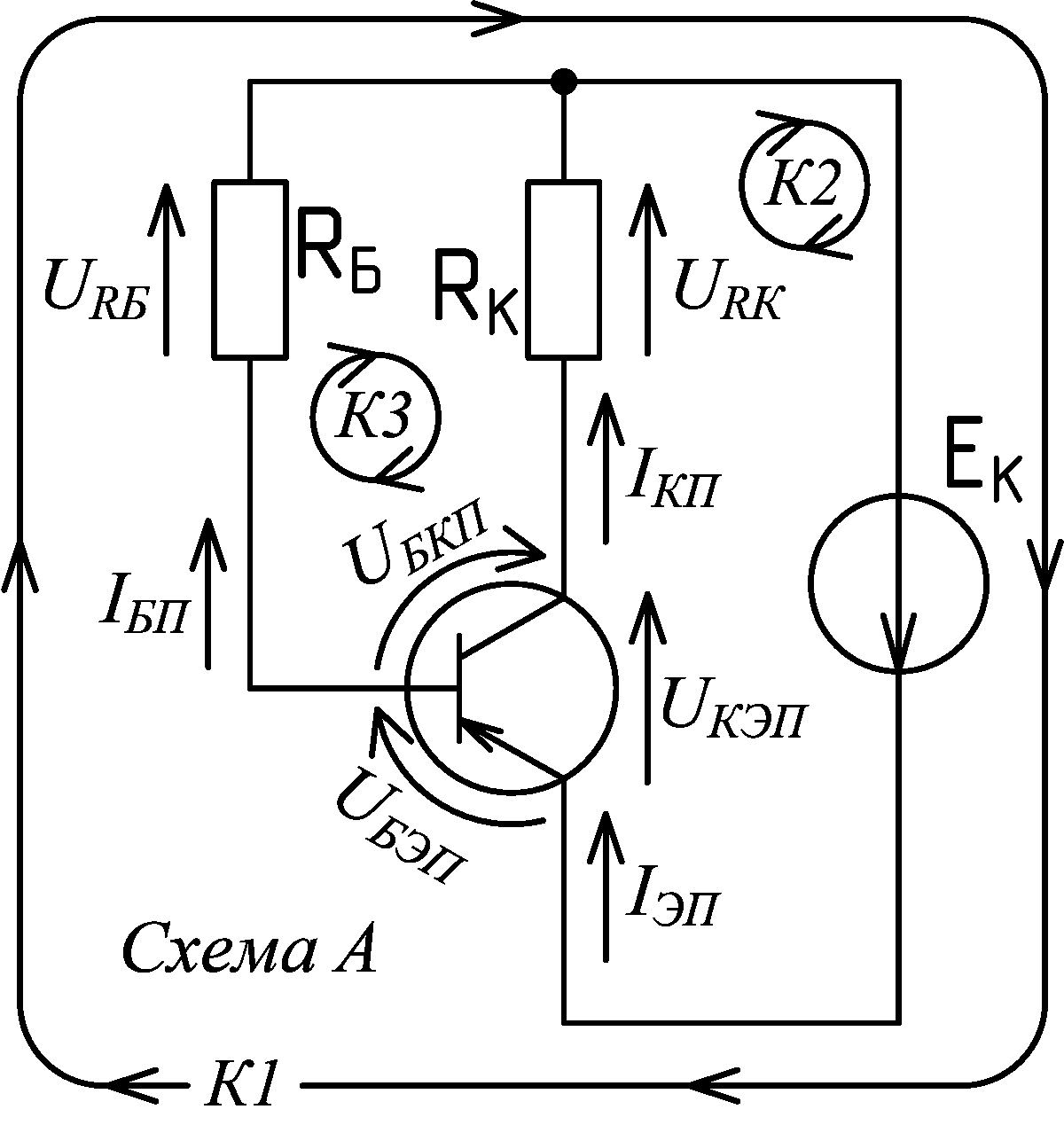
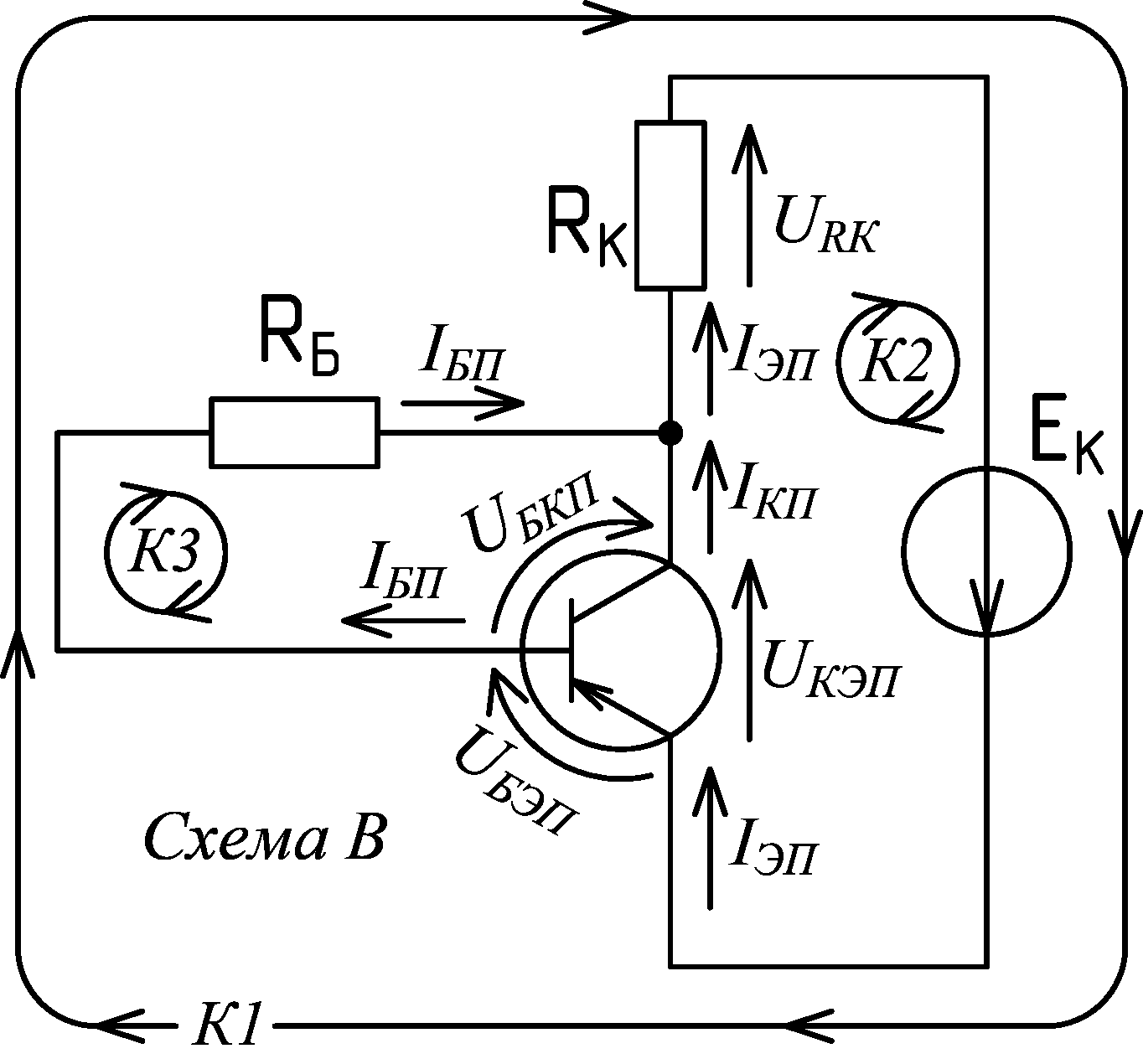
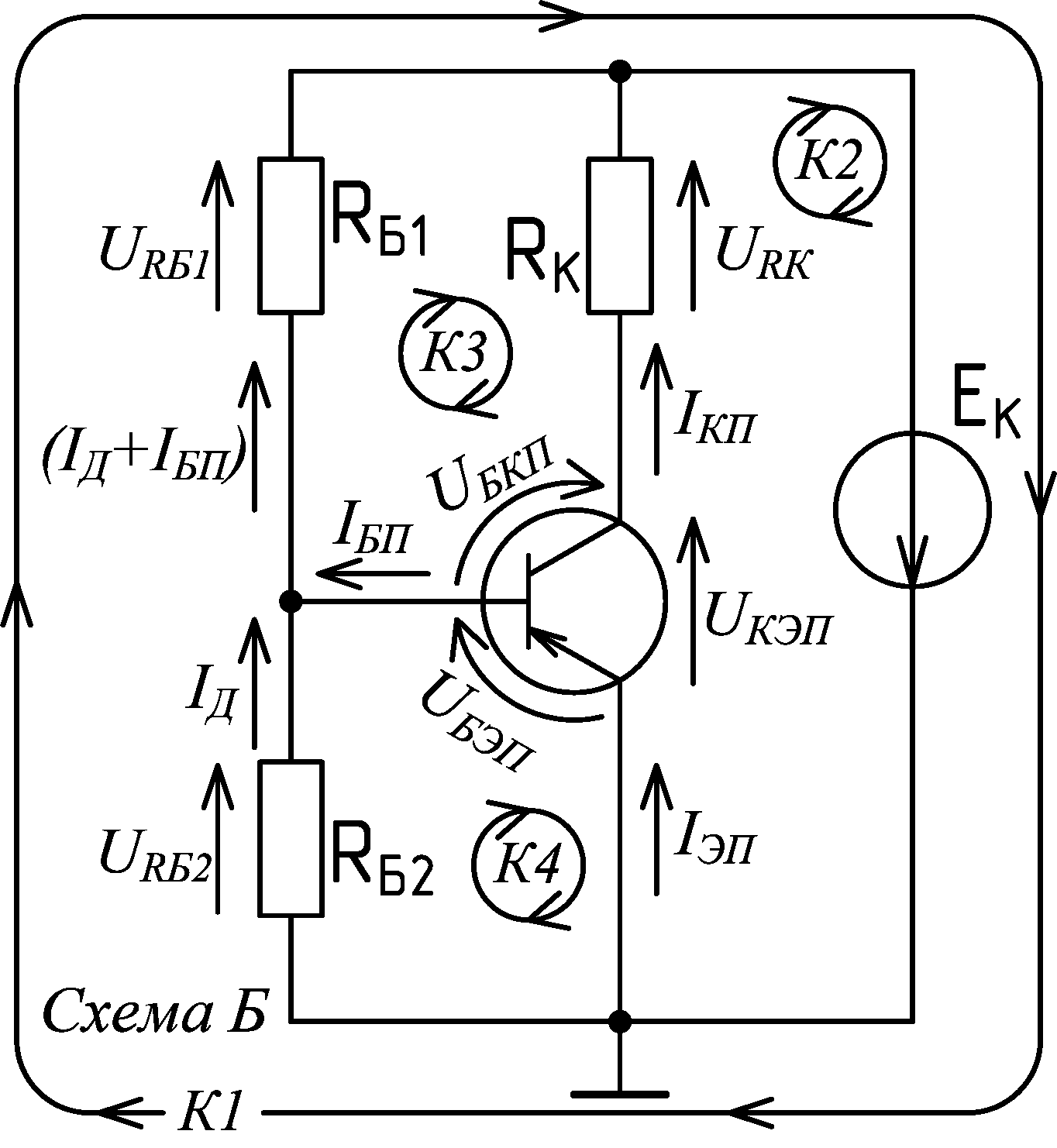
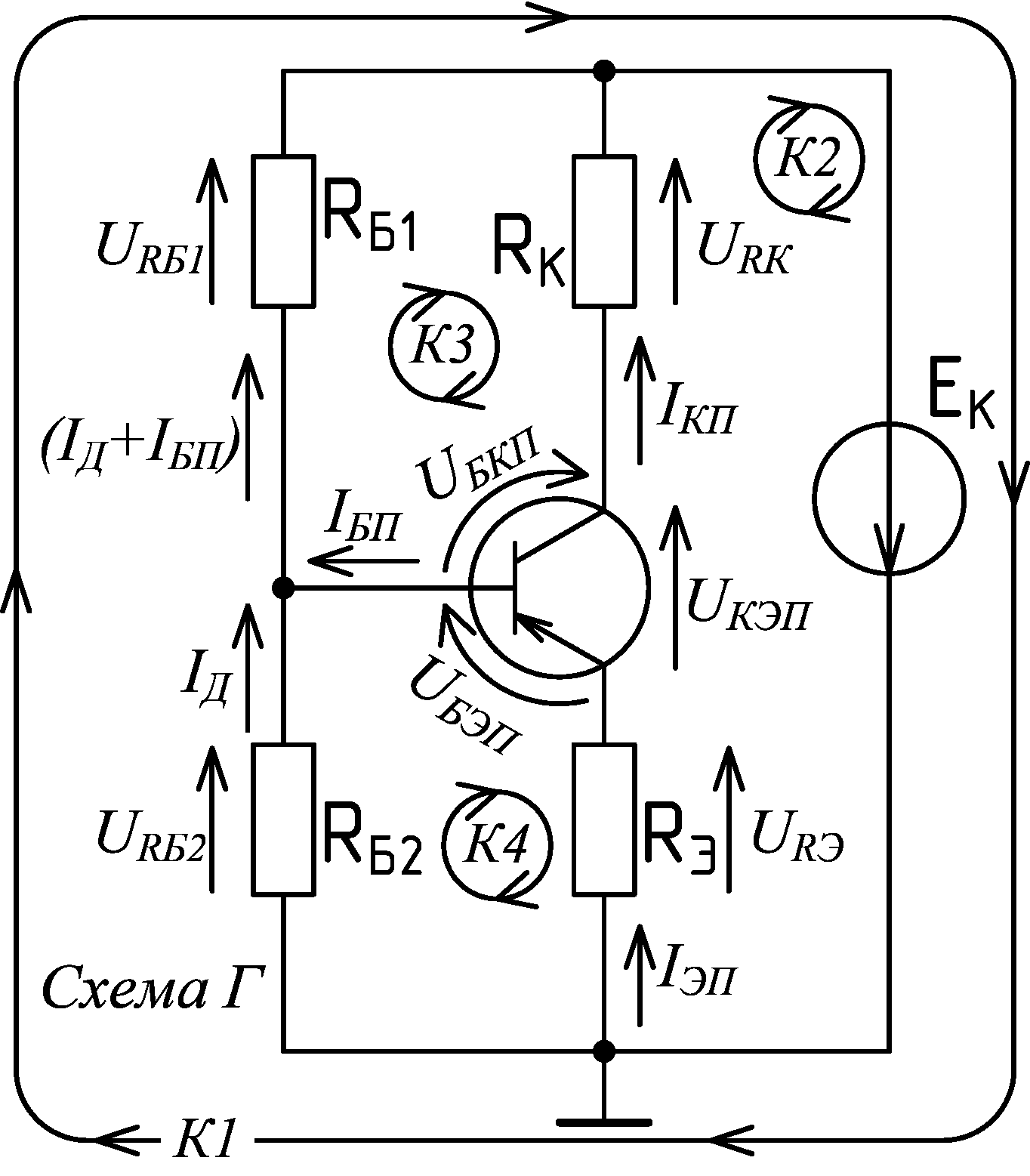
Практические занятия по дисциплине «Расчет электронных схем» на тему: Решение задач на аналитический расчёт режима покоя транзисторных каскадов с общим эмиттером. Версия от 21.10.2020 Схемы к задачам:
На схемах приведены действительные направления токов и напряжений для активного режима работы биполярного транзистора структуры p‑n‑p. Если в схемах будет применяться транзистор структуры n‑p‑n, тогда все действительные направления токов и напряжений и полярности источников питания должны быть заменены на противоположные.
Требования к решению задач:1. При записи результатов вычислений применять приставки кратных и дольных единиц международной системы единиц. Ознакомиться с ними можно по статье в википедии «Приставки СИ». Основное замечание в том, что нужны не все приставки, а только «инженерные» (по степени числа 10 кратной трём) и в диапазоне от 10-12 до 109. В решении задач следует применять только русские обозначения, но надо знать также и международные, поскольку они часто используются при маркировке радиодеталей, в обозначении номиналов на принципиальных схемах и т.д. 2. При выполнении расчётов необходимо обеспечивать инженерную точность вычислений, для этого все промежуточные и конечные результаты округлять до четырёх значащих цифр. Про суть этого требования хорошо изложено в статье википедии «Округление» в разделе «Округление при работе с числами ограниченной точности». Про значащие цифры подробно написано в статье: «https://studfile.net/preview/1757786/page:3/». 3. Оформлять решение необходимо следующим образом: 3.1. Обязательно в каждой задаче рисовать принципиальную схему с обозначением действительных направлений токов и напряжений и выбранных направлений обхода контуров. 3.2. К каждому приведённому уравнению должна предшествовать словесная запись, по какому закону (и для какого контура) это уравнение было получено. 3.3. Вычисления искомых величин и промежуточные вычисления осуществляются сначала через преобразование уравнений в общем виде для выражения нужных величин. Затем в эти уравнения подставляются значения величин, выраженные в единицах СИ (амперах, вольтах, омах), т.е. приставки единиц заменяются соответствующими порядками, а сами единицы опускаются. 3.4. Вычисленные значения преобразовываются к удобному для воспроизведения формату, т.е. они записывается с применением инженерных приставок СИ с целью уменьшения числа цифр в полученном результате. 3.5. Вычисленные значения искомых величин и сами эти величины просто подчёркиваются карандашом или цветной ручкой в тексте решения. Отдельно их записывать как «Ответ» не нужно. Пример решения задачи №27.1:По первому закону Кирхгоффа для биполярного транзистора в активном режиме: IЭП = IКП + IБП (1) По второму закону Кирхгоффа для биполярного транзистора в активном режиме: UКЭП = UБЭП + UБКП (2) Для биполярного транзистора в активном режиме статический коэффициент передачи тока базы в схеме с общим эмиттером определяется по формуле: β = IКП / IБП (3) Первые три уравнения, приведённые выше, будут одинаковыми для всех четырёх схем, поскольку в усилительных каскадах транзистор работает в активном режиме. Вид остальных уравнений будет зависеть от схемы. По второму закону Кирхгоффа для контура 1: IЭП ·0 + UБЭП + URБ = EК В полученном уравнении IЭП протекает по ветви с нулевым сопротивлением, поэтому не создаёт падение напряжения, поэтому первое слагаемое отбрасываем. Третье слагаемое записываем по закону Ома, т.е. URБ = IБП·RБ . Отсюда следует: UБЭП + IБП·RБ = EК (4) Уравнение по второму закону Кирхгоффа для контура 2 (и все остальные) следует записывать сразу с применением закона Ома: UКЭП + IКП·RК = EК (5) Обозначения напряжений на резисторах в схемах лучше не приводить, чтобы не загромождать их. Они приведены только для понимания, поскольку токи и напряжения на резисторах всегда сонаправлены. Также, существуют несколько экзаменационных задач, в которых фигурирует только напряжение на резисторе, а его ток неизвестен. Соответственно, если напряжения резисторов не указываются, то токи резисторов и их направления указывать на схемах обязательно. По второму закону Кирхгоффа для контура 3: IБП·RБ – UБКП – IКП·RК = 0 , отсюда следует что: IБП·RБ = UБКП + IКП·RК (6) Полученные уравнения с (1) по (6) исчерпывающе описывают электрические свойства схемы, поэтому чтобы найти решение задачи, необходимо, для начала, проанализировать «дано». Для этого все известные, по условию задачи, величины в полученных уравнениях подчёркиваются, а над искомыми величинами ставится знак вопроса. После этого решение задачи становится достаточно очевидным. Важное замечание! Значительно упрощается решение задач, если в «дано» приведены какие-либо два параметра по току, т.е. одни из следующих параметров: β , IБП , IКП или IЭП . В этом случае все остальные токи схемы можно выразить и рассчитать по двум уравнениям (1) и (3). Только для этого в схемах Б и Г должно быть дополнительно приведено соотношение между током базы и током делителя (IД = 5·IБП) и обычно это так и есть, хотя бывают задачи, в которых это соотношение в «дано» не приводится. В задаче №27.1 известны два параметра по току IКП и β, поэтому можно считать все токи схемы известными. Величина EК находится по уравнению (5), а величина IБП находится по уравнению (3). Пример оформление решения: 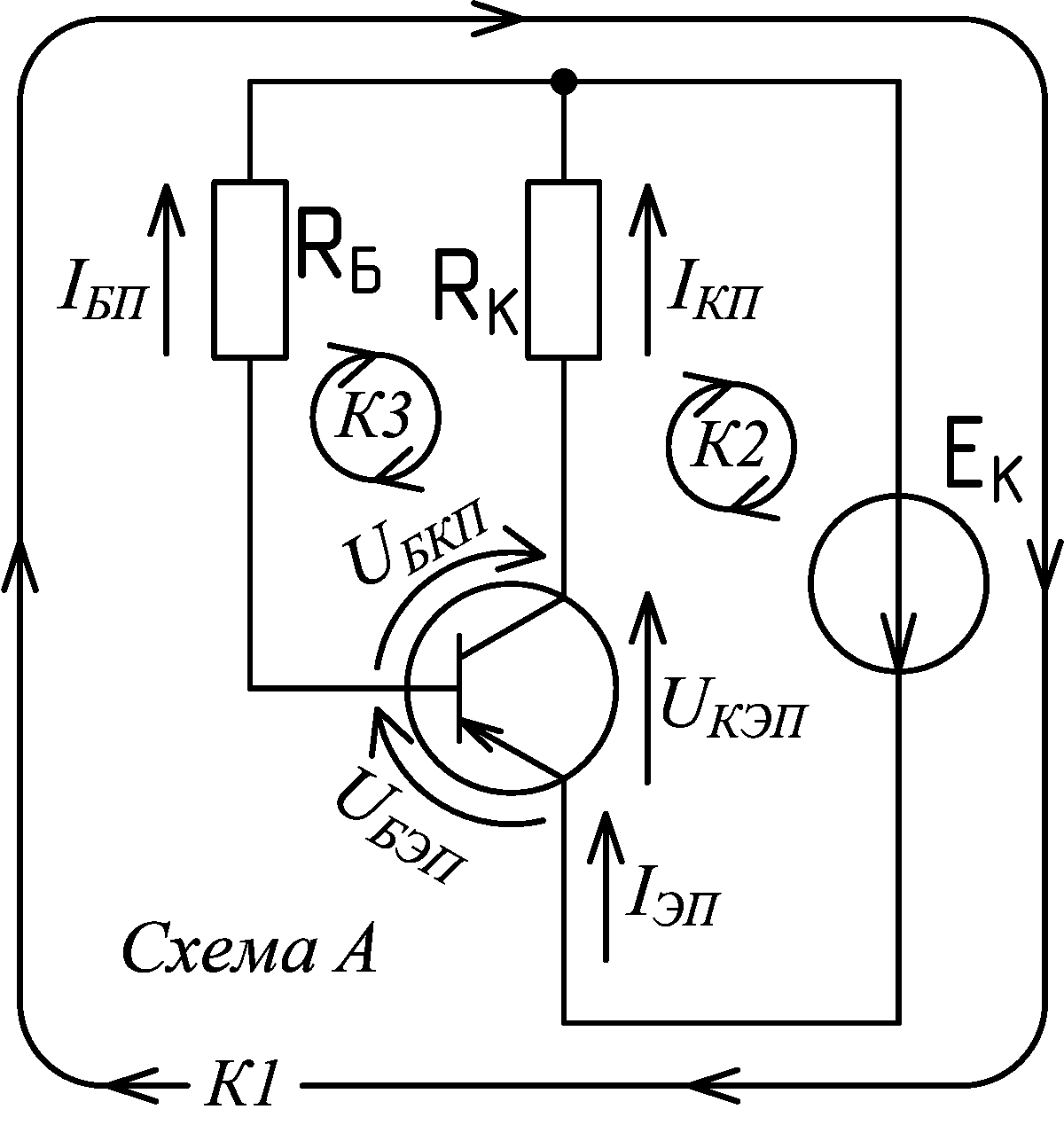 Дано: Схема А, UКЭП = 8 В, IКП = 24 мА, RК = 2.2 кОм, β = 105 Найти: EК , IБП Решение: По 2ЗК для К1: EК= UКЭП + IКП·RК = 8 + 24·10-3·2.2·103 = 8 + 24·2.2 = 60.8 В Для БТ в АР: β = IКП / IБП => IБП= IКП / β = (24·10-3)/105 = 228.6·10-6 = 228.6 мкА Пример решения задачи №27.2: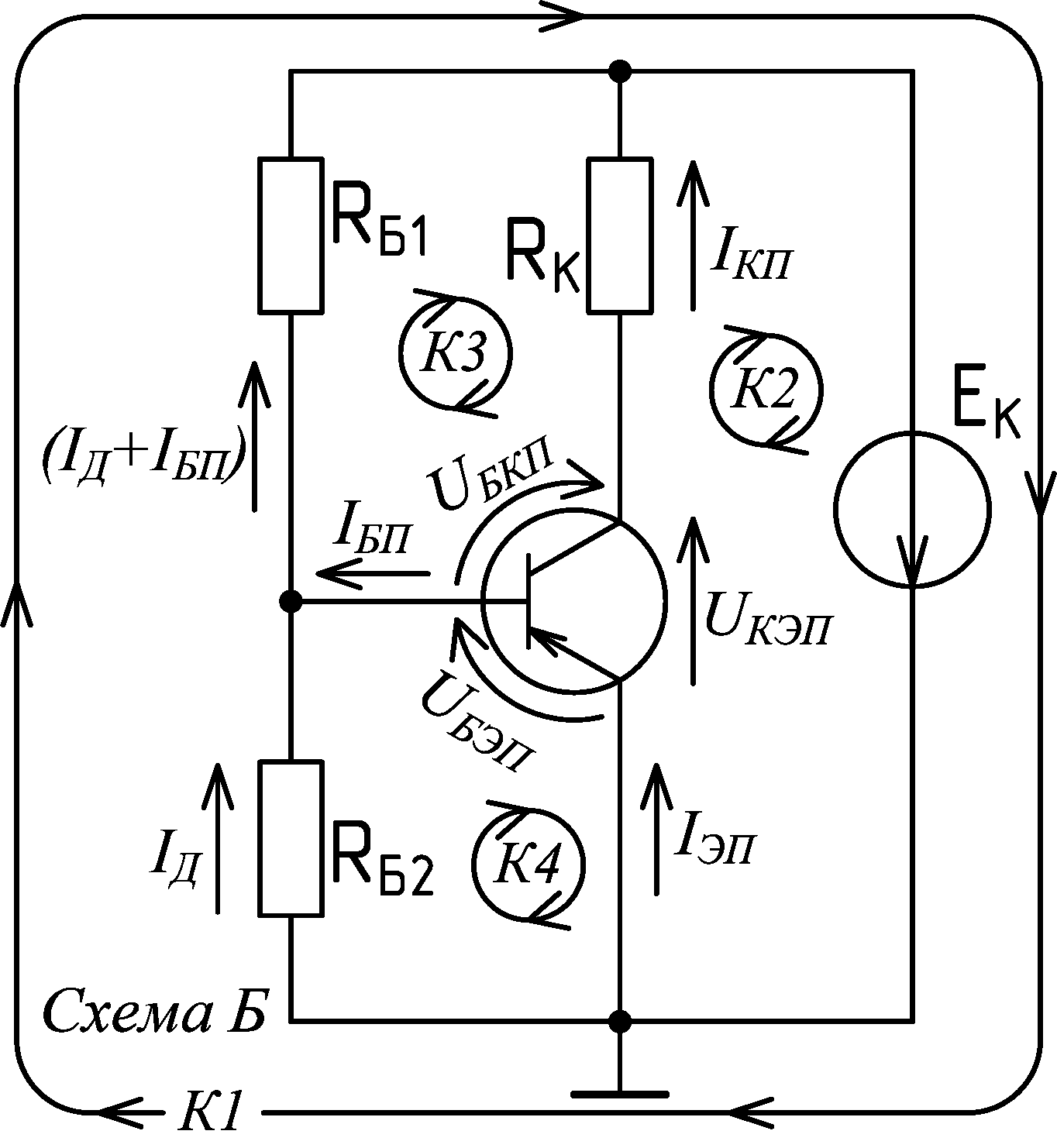 Дано: Схема Б, EК = 44 В, RБ1 = 2.2 кОм, RБ2 = 3.8 кОм, β = 52, IД = 5·IБП Найти: IБП , IКП Решение: По 1ЗК для БТ в АР: IЭП = IКП + IБП (1) По 2ЗК для БТ в АР: UКЭП = UБЭП + UБКП (2) Для БТ в АР: β = IКП / IБП (3) В данной схеме, ток резистора RБ2 обозначен как ток делителя IД , поскольку резисторы RБ1 и RБ2 являются резистивным делителем напряжения источника питания EК до напряжения базы покоя UБЭП . Чтобы не вводить дополнительное обозначение и упростить расчёты, ток резистора RБ1 подписан на схеме в соответствии с первым законом Кирхгофа для узла, подключённого к базе транзистора, т.е. IRБ1 = IД + IБП . По 2ЗК для К1: IД·RБ2 + (IД + IБП)·RБ1 = EК (7) К2: UКЭП + IКП·RК = EК (8) К3: (IД + IБП)·RБ1 – IКП·RК – UБКП = 0 , => => (IД + IБП)·RБ1 = UБКП + IКП·RК (9) В задаче №27.2 даны только один параметр по току (β) и соотношение между током базы и током делителя (IД = 5·IБП), поэтому все токи в схеме остаются неизвестными. Это и понятно, поскольку по условию задачи эти токи надо найти. Полученные уравнения с (1) по (3) и с (7) по (9) исчерпывающе описывают электрические свойства схемы, поэтому чтобы найти решение задачи, необходимо, для начала, проанализировать «дано». Для этого все известные, по условию задачи, величины в полученных уравнениях подчёркиваются, а над искомыми величинами ставится знак вопроса. После этого решение задачи становится достаточно очевидным. Решение задачи выполняется по уравнению (7), в которое подставляется соотношение IД = 5·IБП , затем из этого уравнения выражается и находится IБП . Величина IКП выражается и находится из уравнения (3). По 2ЗК для К1: IД·RБ2 + (IД + IБП)·RБ1 = EК , => 5·IБП·RБ2 + (5·IБП + IБП)·RБ1 = EК , => => 5·IБП·RБ2 + 6·IБП·RБ1 = EК , => IБП·(5·RБ2 + 6·RБ1) = EК , => => IБП= EК /(5·RБ2 + 6·RБ1) = 44/(5·3.8·103 + 6·2.2·103) = 1.366·10-3 = 1.366 мА Для БТ в АР: β = IКП / IБП => IКП= β·IБП = 52·1.366·10-3 = 71.03·10-3 =71.03 мА Следует обратить внимание на то, что из-за единственного округления числа 1.366·10-3 при промежуточном вычислении, в ответе присутствует вычислительная погрешность: 71.03 мА вместо точного 71.06 мА. Относительная погрешность мала и, поэтому, допустима, но она накапливается, если будет много промежуточных вычислений. Пример решения задачи №27.3: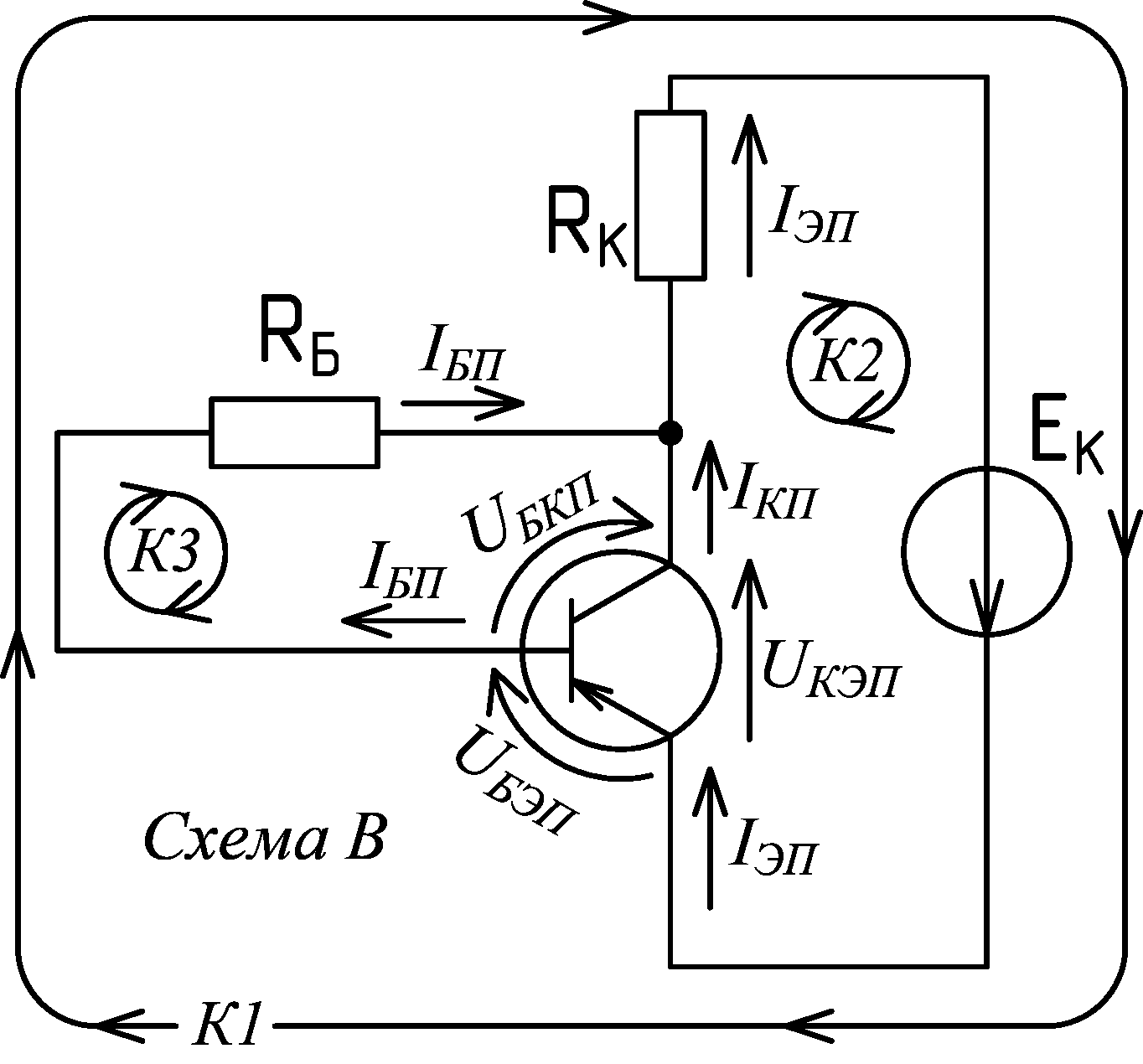 Дано: Схема В, UКЭП = 15.2 В, UБЭП = 0.38 В, RБ = 3.5 кОм, RК = 76 Ом, EК = 28 В Найти: β Решение: По 1ЗК для БТ в АР: IЭП = IКП + IБП (1) По 2ЗК для БТ в АР: UКЭП = UБЭП + UБКП (2) Для БТ в АР: β = IКП / IБП (3) Необходимо обратить особое внимание на отличительную особенность этой схемы, которая заключается в том, что через резистор RК протекает не ток коллектора IКП , а ток эмиттера IЭП ! Для понимания этого, можно записать уравнение по первому закону Кирхгофа для единственного узла схемы, это уравнение будет таким же, как и (1). По 2ЗК для К1: UБЭП + IБП·RБ + IЭП·RК = EК (10) К2: UКЭП + IЭП·RК = EК (11) К3: IБП·RБ – UБКП = 0 , => => IБП·RБ = UБКП (12) В задаче №27.2 не даны параметры по току и требуется найти β, т.е. необходимо определить токи базы и коллектора для решения по уравнению (3). Подчёркиваем все известные по условию задачи величины в уравнениях (1), (2), (3), (10), (11) и (12), а над искомыми величинами IКП и IБП ставим знак вопроса, после этого ищем решение. Способ 1. Сначала выражается и находится ток IЭП из уравнения (11), после чего можно выразить и найти ток IБП из уравнения (10). Из полученных токов определяется величина IКП по уравнению (1), а затем рассчитывается β по уравнению (3). По 2ЗК для К2: UКЭП + IЭП·RК = EК , => IЭП·RК = EК – UКЭП , => => IЭП = (EК – UКЭП)/RК = (28 – 15.2)/76 = 168.4·10-3 = 168.4 мА По 2ЗК для К1: UБЭП + IБП·RБ + IЭП·RК = EК , => IБП·RБ = EК – UБЭП – IЭП·RК , => => IБП·= (EК – UБЭП – IЭП·RК)/RБ = (28 – 0.38 – 168.4·10-3·76)/(3.5·103) = 4.235·10-3 = 4.235 мА По 1ЗК для БТ в АР: IЭП = IКП + IБП , => => IКП = IЭП – IБП = 168.4·10-3– 4.235·10-3 = 164.2·10-3 = 164.2 мА Для БТ в АР: β = IКП / IБП = 164.2·10-3/4.235·10-3 = 38.77 Способ 2. Сначала из уравнения (2) выражается и находится напряжение UБКП , затем оно подставляется в уравнение (12) для определения тока IБП. Подставляя в уравнение (11) вместо тока IЭП уравнение (1) можно выразить и определить ток IКП. Из полученных токов рассчитывается β по уравнению (3). По 2ЗК для БТ в АР: UКЭП = UБЭП + UБКП , => UБКП = UКЭП – UБЭП По 2ЗК для К3: IБП·RБ = UБКП , подставляем сюда вместо UБКП полученное выше уравнение => => IБП·RБ = UКЭП – UБЭП , => IБП = (UКЭП – UБЭП)/RБ = (15.2 – 0.38)/(3.5·103) = 4.234·10-3 = 4.234 мА По 1ЗК для БТ в АР: IЭП = IКП + IБП По 2ЗК для К2: UКЭП + IЭП·RК = EК , подставляем сюда вместо IЭП записанное выше уравнение => => UКЭП + (IКП + IБП)·RК = EК , => UКЭП + IКП·RК + IБП·RК = EК , => IКП·RК = EК – UКЭП – IБП·RК , => => IКП = (EК – UКЭП – IБП·RК)/RК = (28 – 15.2 – 4.234·10-3·76)/76 = 164.2·10-3 = 164.2 мА Для БТ в АР: β = IКП / IБП = 164.2·10-3/4.234·10-3 = 38.78 Пример решения задачи №27.4: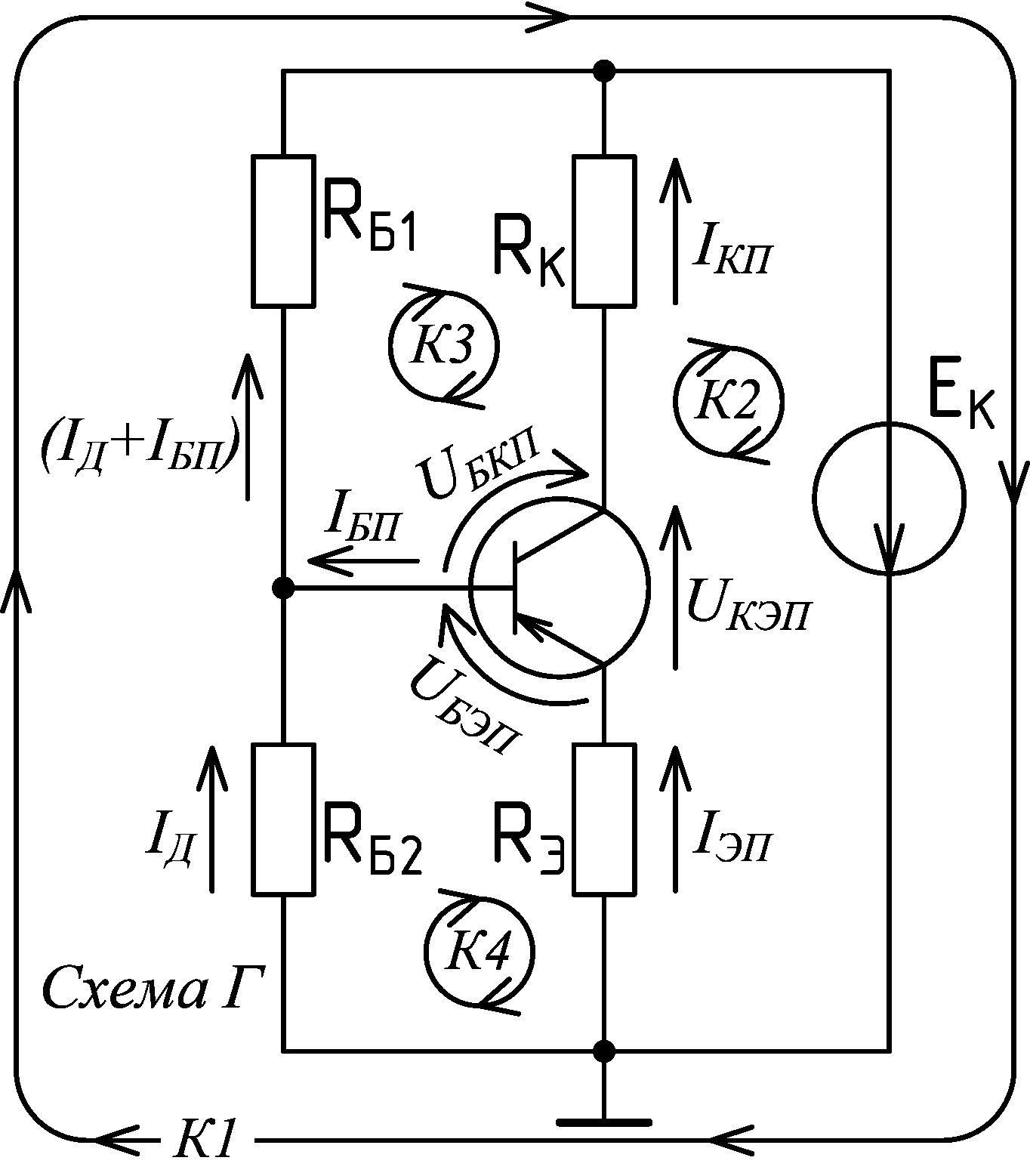 Дано: Схема Г, IБП = 75 мкА, IД = 5·IБП, β = 38, RБ1 = 43 кОм, RК = 3.5 кОм, RЭ = 12 Ом, UКЭП = 10 В Найти: EК , RБ2 , UБЭП Решение: По 1ЗК для БТ в АР: IЭП = IКП + IБП (1) По 2ЗК для БТ в АР: UКЭП = UБЭП + UБКП (2) Для БТ в АР: β = IКП / IБП (3) В данной схеме, ток резистора RБ2 обозначен как ток делителя IД , поскольку резисторы RБ1 и RБ2 являются резистивным делителем напряжения источника питания EК до напряжения базы покоя UБП = UБЭП + URЭ . Чтобы не вводить дополнительное обозначение и упростить расчёты, ток резистора RБ1 подписан на схеме в соответствии с первым законом Кирхгофа для узла, подключённого к базе транзистора, т.е. IRБ1 = IД + IБП . По 2ЗК для К1: IД·RБ2 + (IД + IБП)·RБ1 = EК (13) К2: IЭП·RЭ + UКЭП + IКП·RК = EК (14) К3: (IД + IБП)·RБ1 – IКП·RК – UБКП = 0 , => => (IД + IБП)·RБ1 = UБКП + IКП·RК (15) К4: IД·RБ2 – UБЭП – IЭП·RЭ = 0 , => => IД·RБ2 = UБЭП + IЭП·RЭ (16) В задаче №27.4 даны два параметра по току (IБП и β) и соотношение между током базы и током делителя (IД = 5·IБП), поэтому все токи в схеме можно считать известными, т.к. они легко выражаются из уравнений (1) и (3) при такой необходимости. Подчёркиваем все известные по условию задачи величины в уравнениях (1), (2), (3), (13), (14), (15) и (16), а над искомыми величинами EК , RБ2 и UБЭП ставим знак вопроса, после этого ищем решение. Величину EК можно определить из уравнения (14), если предварительно выразить токи IЭП и IКП . Величина RБ2 выражается из уравнения (13) и соотношения IД = 5·IБП . Величина UБЭП определяется из уравнения (16). Для БТ в АР: β = IКП / IБП , => => IКП = β·IБП (17) По 1ЗК для БТ в АР: IЭП = IКП + IБП , подставляем сюда вместо IКП уравнение (17) => => IЭП = β·IБП + IБП , => => IЭП = IБП·(β +1) (18) По 2ЗК для К2: EК = IЭП·RЭ + UКЭП + IКП·RК , подставляя сюда уравнения (18) и (17) => => EК = IБП·(β +1)·RЭ + UКЭП + β·IБП·RК = 75·10-6·(38 +1)·12 + 10 + 38·75·10-6·3.5·103 = 20.01 В По 2ЗК для К1: IД·RБ2 + (IД + IБП)·RБ1 = EК , => 5·IБП·RБ2 + (5·IБП + IБП)·RБ1 = EК => => 5·IБП·RБ2 + 6·IБП·RБ1 = EК => 5·IБП·RБ2 = EК – 6·IБП·RБ1 => => RБ2= (EК – 6·IБП·RБ1)/(5·IБП) = (20.01 – 6·75·10-6·43·103)/(5·75·10-6) = 1.76·103 = 1.76 кОм По 2ЗК для К4: IД·RБ2 = UБЭП + IЭП·RЭ => UБЭП = IД·RБ2 – IЭП·RЭ , подставляя сюда уравнение (18) и соотношение IД = 5·IБП => => UБЭП= 5·IБП·RБ2 – IБП·(β +1)·RЭ = 5·75·10-6·1.76·103 – 75·10-6·(38 +1)·12 = 624.9·10-3 = 624.9 мВ |