Технология Монахова. Тишина Татьяна_ Технология Монахова. Решение задач на вычисление и доказательство с использованием изученных формул. Планируемые результаты
 Скачать 1.94 Mb. Скачать 1.94 Mb.
|
|
План деятельности учащихся 8-ого класса по геометрии по изучению темы «Площадь» по учебнику Л.С. Атанасян и др. (14 часов) Содержание курса: Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Площадь многоугольника. Решение задач на вычисление и доказательство с использованием изученных формул. Планируемые результаты:
Характеристика основных видов деятельности ученика: Объяснять, как производится измерение площадей многоугольников, какие многоугольники называются равновеликими и какие равносоставленными Формулировать основные свойства площадей и выводить с их помощью формулы площадей прямоугольника, параллелограмма, треугольника, трапеции Формулировать и доказывать теорему об отношении площадей треугольника, имеющих по равному углу. Формулировать и доказывать теорему Пифагора и обратную ей Решать задачи на вычисление и доказательство, связанные с формулами площадей и теоремой Пифагора. В.1. Знать понятие площадь многоугольника, основные свойства площадей. Уметь применять основные свойства площадей. В.2. Знать формулу площади прямоугольника. Уметь решать задачи на нахождение площади прямоугольника. В.3. Знать, что такое высота, проведенная к основанию (стороне), формулу площади параллелограмма. Уметь решать задачи на нахождение площадь параллелограмма. В.4. Знать формулы площади треугольника. Уметь решать задачи на нахождение площади треугольника. В.5. Знать формулу площади трапеции. Уметь решать задачи на нахождение площади трапеции. В.6. Знать теорему Пифагора и теорему обратную теореме Пифагора, египетский треугольник. Уметь применять теорему Пифагора и теорему обратную теореме Пифагора, египетский треугольник для решения задач.
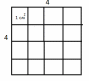
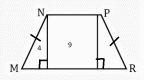
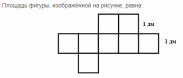
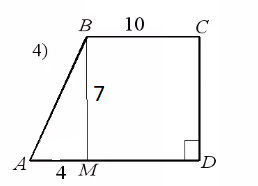
В.1. Знать понятие площадь многоугольника, основные свойства площадей. Уметь применять основные свойства площадей. Д.1. №1. Найдите площадь квадрата, изображенного на рисунке: 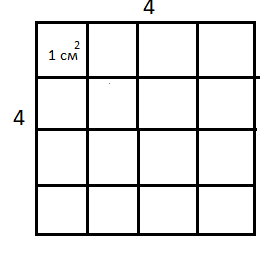 №2. Найдите площадь квадрата, сторона которого равна 3,2 см. №3. Найдите площадь изображенной фигуры: 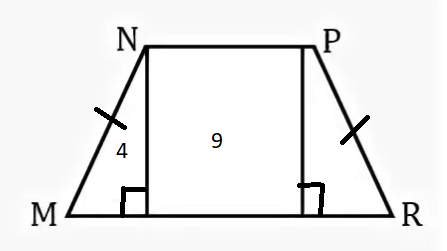 №4. Найдите сумму площадей квадратов, построенных на сторонах прямоугольника со сторонами 5см и 7 см. Ошибки: Не знает свойства площадей многоугольников. Площадь квадрата. Перенос знаний на другую фигуру. Д.з.1. Стандарт: №445, 446   Хорошо: Сколько нужно квадратов со стороной 2 см, чтобы покрыть поверхность прямоугольника с длиной 24 см и шириной 8 см? Периметр квадрата равен 24 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 9 см. Чему равен периметр прямоугольника? Отлично: Сторона квадрата равна 5 см. Если сторона удвоится, то во сколько раз площадь нового квадрата станет больше, чем площадь старого квадрата? Найдите сумму площадей квадратов, построенных на сторонах прямоугольника со сторонами 4 см и 9 см. К.1. Найдите площадь квадрата, если его сторона равна а) 1, 4 см б) 2,8 см в) 3,2 см г) 4,5 см. Найдите сторону квадрата, если его площадь равна а) 64 см2 б) 25 см2 в) 49 см2 г) 36 см2. Найдите периметр квадрата, если его площадь равна а) 16 см2 б) 100 см2 в) 81 см2 г) 64 см2 4. 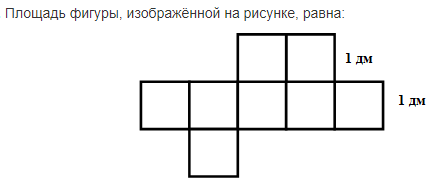 В.2. Знать формулу площади прямоугольника. Уметь решать задачи на нахождение площади прямоугольника. Д.2. №1. Найдите площадь прямоугольника, стороны которого равны 3,2 см и 5,7 см. №2. Смежные стороны прямоугольника равны 4,2 см и 3,5 см. Найдите площадь этого прямоугольника. №3. Найдите площадь многоугольника, изображенного на рисунке, все углы которого прямые. 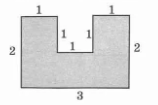 №4. Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равно 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола? Ошибки: Не знает формулы площади квадрата и прямоугольника Не знает, что такое смежные стороны Применение свойств площади многоугольника Перенос знаний на реальную ситуацию Д.з.2. Стандарт: №452  Хорошо: №454  Отлично: 456, 457, 458  К.2. Найдите площадь прямоугольника, если его смежные стороны равны а) 4, 2 см и 3,5 см б) 1,8 см и 3,2 см в) 2,5см и 1,6см г) 4,6см и 1,5см. Найдите сторону a прямоугольника, если известна S – площадь прямоугольника и b – сторона прямоугольника a) S=192, b = 12 б) S = 408, b = 24 в) S = 494, b = 19 г) S = 442, b = 13.. Найдите площадь прямоугольника, если одна из его сторон равна 10см, а периметр равен а) 48 см б) 36 см в) 52 см г) 64 см. В.3. Знать, что такое высота, проведенная к основанию (стороне), формулу площади параллелограмма. Уметь решать задачи на нахождение площадь параллелограмма. Д.3. №1. Найдите площадь параллелограмма, если основание равно 16 см, а высота 9 см. №2. Найдите площадь параллелограмма, если одна из его сторон равна 7 см, а высота, проведенная к этой стороне, равна 4 см. №3. Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма. №4. Стороны параллелограмма равны 10 см и 85 см. Высота, опущенная на меньшую сторону, равна 51 см. Найдите высоту, опущенную на большую сторону. Ошибки: Формула площади параллелограмма Не может правильно провести высоту Понятие угла между сторонами Не видит смежные углы Свойства площадей К тексту задачи не может правильно сделать рисунок Д.з.3. Стандарт: 459, 464  Хорошо: 460, 461, 463  Отлично: 465, 466  К.3. 1. Найти основание параллелограмма, если его площадь равна 23 м2, а высота 5м. 1) 4,6 м 2) 115 м 3) 18 м 4) 28 м 2. Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма. 3. Площадь параллелограмма равна 72 см2, основание равно 4 см. Найдите высоту параллелограмма. 4. Высота параллелограмма, проведенная к стороне равна 7, а площадь 105 см2. Найдите эту сторону. В.4. Знать формулы площади треугольника. Уметь решать задачи на нахождение площади треугольника. Д.4. №1. Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника. №2. Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника. №3. Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника. №4. Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катет 8 см, а гипотенуза равна 10 см Ошибки: Формула площади треугольника Не знает виды треугольников Медиана, высота, биссектриса Проведение высоты к стороне К задачи не может правильно сделать рисунок Д.з. 4 Стандарт: 468,, 471, 475  Хорошо: 469, 470  Отлично: 472,473, 476, 479  К.4. 1. Сторона треугольника равна 18 см, а высота, проведенная к ней, в 3 раза меньше стороны. Найдите площадь треугольника. 2. Найдите площадь треугольника, сторона которого равна 8 см, а высота, проведенная к ней, - 2,8 см. 3. Найдите площадь прямоугольного треугольника, если его катеты равны 23 см и 32 см. 4. Площадь треугольника равна 48 см2, а одна из его сторон – 4 см. Найдите высоту треугольника, проведенную к данной стороне. В.5. Знать формулу площади трапеции. Уметь решать задачи на нахождение площади трапеции. Д.5. №1. Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции. №2. Найдите площадь трапеции изображенной на рисунке: 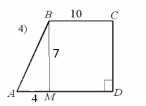 №3. Найдите площадь равнобедренной трапеции, если ее основания равны 4 см и 10 см , а острый угол 45◦ №4. В прямоугольной трапеции меньшая боковая сторона равна 6см и составляет с меньшей диагональю угол 45◦ . Острый угол трапеции также равен 45◦. Найдите площадь трапеции. Ошибки: Формула площади трапеции Виды трапеции Не знает, что такое основания в трапеции К задачи не может правильно сделать рисунок Д,з.5. Стандарт: 480  Хорошо: 481,527 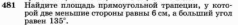 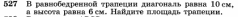 Отлично: 482, 518, 522,   К.5. 1. Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции. 2. Найдите площадь трапеции, основания которой равны 11 см и 17 см, а высота – 8 см. 3. Площадь трапеции равна 24 см2. Найдите сумму оснований, если ее высота равна 6 см. 4. Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см. В.6. Знать теорему Пифагора и теорему обратную теореме Пифагора, египетский треугольник. Уметь применять теорему Пифагора и теорему обратную теореме Пифагора, египетский треугольник для решения задач. Д.6. №1. Найдите гипотенузу, если катеты равны 2см и 5 см. №2. Найдите второй катет прямоугольного треугольника, если известно, что первый катет равен 9 см, а гипотенуза 15 см. №3. Найдите сторону ромба, если его диагонали равны 6 см и 8см. №4. Найдите меньшую высоту треугольника со сторонами 15, 20, 25. Ошибки: Не знает теорему Пифагора Обратную теорему Пифагора Прямоугольный треугольник Д.з. 6. Стандарт: 483, 484, 485, 486, 498  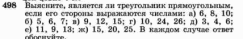 Хорошо: 487, 488, 490, 491, 493  Отлично: 489, 496,497, 499   К.6. 1. В треугольнике ABC: ∠C=90∘, AB=8 и BC=5. Найдите квадрат AC. 2. Может ли прямоугольный треугольник иметь стороны: А) 3, 4, 5 б) 8, 6, 10 в) 5, 10, 10 3. Дан прямоугольный треугольник ABC, ∠C=90∘, и AC=3, BC=4. Найдите длину AB. 4. Есть прямоугольный треугольник ABC, где ∠C=90∘, и AC=7, AB=25. Найдите длину BC. 5. В прямоугольном треугольнике ABC, ∠C=90∘, и AC=8, BC=15. Найдите длину AB. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||