Документ Microsoft Word. Решение задач по дисциплине Статистика

• Название: Решение задач по дисциплине Статистика
• Дата: 15.04.2021
• Размер: 24.88 Kb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Решение; #194911

Решение задач

по дисциплине: «Статистика»

Выполнил:

Проверил:

2021
Содержание

Задача 6.1. ………………………………………………………….3

Задача 6.2. ……………………………………………………….…4

Список использованной литературы…………………..6

6. Задачи по теме ИЗУЧЕНИЕ ВАРИАЦИИ

При решении задач ввести условные обозначения (Дано), привести формулы расчета и ход решения.

Задача 6.1. При разработке материалов учета городского населения было установлено, что 16% жителей – пожилые люди (из общей численности населения города 100 тыс. человек методом случайного бесповторного отбора было обследовано 200 человек).

С вероятностью 95,4% определите предел, в котором находится доля жителей города пожилого возраста.
Дано:

Случайный бесповторный отбор;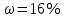

;

n = 200 человек;

N = 100 000 человек;

P = 95,4% (вероятность).
Решение:

Рассчитаем среднюю ошибку выборочной доли по формул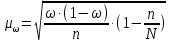е:

, где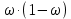

– дисперсия доли в выборочной совокупности;

n – численность выборки;

N – объем генеральной совокупности.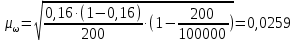


Предельная ошибка выборочной доли рассчитывается по формул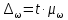е:

, где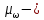

средняя ошибку выборочной доли;

t – коэффициент доверия.

При вероятности 0,954 табличное значение t составляет 2.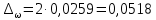

или 5,18%.

С вероятностью 0,954 можно утверждать, что доля жителей города пожилого возраста колеблется в пределах: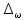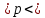

ω - ω +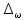

0,16-0,0518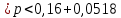

0,1082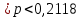

Вывод: с вероятностью 95,4% можно утверждать, что доля жителей города пожилого возраста колеблется от 10,82 до 21,18%.
Задача 6.2. В коммерческих банках города 10250 клиентов – физические лица. Методом случайного бесповторного отбора предполагается определить долю вкладчиков с размером вклада 100 тыс. руб. и более.

Какова должна быть численность выборки, чтобы с вероятностью 95% ошибка выборки не превышала 2%, если на основе предыдущих обследований известно, что доля таких вкладчиков составляет 8%?

Как изменится численность выборки, если вероятность, гарантирующую результат, увеличить до 99,7%?
Дано:

ω = 0,08 или 8%;

N = 10250 клиентов;

P = 95% и 99,7%.


Решение:

При случайном бесповторном отборе для расчета не­обходимой численности выборки для определения доли с заданной точностью, применяется следующая формула:

n = 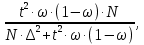где

t – коэффициент доверия,

ω (1 – ω) – дисперсия,

N – численность генеральной совокупности,

Δ – предельная ошибка выборочной доли.

При Р = 0,95, табличное значение t = 2.

n = 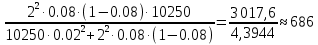чел.

При Р = 0,997, табличное значение t = 3.

n = 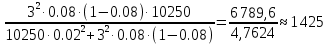чел.

Вывод: численность вкладчиков должна составлять 686 человек;

если вероятность, гарантирующую результат, увеличить до 99,7% то численность выборки увеличится в 2 раза.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. 
   Ниворожкина, Л.И. Статистика: учебник для бакалавров: учебник /. - Москва: Дашков и К: Наука-Спектр, 2019. - 415 с.
   
2. 
   Практикум по теории статистики: учеб. пособие /под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 2019.
   
3. 
   Статистика: учебник/ [Елисеева и др.]. - Москва: Проспект, 2017. -443 с.
   
4. 
   Статистика: учебно-практическое пособие / [Назаров и др.]. - Москва: КноРус, 2018. - 479 с.
   
5. 
   Теория статистики / под ред. проф. Р. А. Шмойловой. – М.: Финансы и статистика, 2018.