Задачи по логистики. Решение задач с помощью ms excel 46

• Название: Решение задач с помощью ms excel 46
• Анкор: Задачи по логистики
• Дата: 14.05.2022
• Размер: 7.4 Mb.
• Имя файла: d0bcd0b5d182d0bed0b4d0b8d187d0bad0b0-d0b4d0bbd18f-d0bfd180d0bed0.docx
• Тип: Решение; #528805
• страница: 13 из 15

ОЦЕНКА ПОТРЕБНОСТИ В ЗАПАСАХ ТОВАРОВ НЕРЕГУЛЯРНОГО СПРОСА

Простейший подход к оценке потребности в запасах това­ров нерегулярного спроса — это анализ количества сде­лок с такими товарами и размера сделок. Рассмотрим один из возможных вариантов такого анализа.

На рис. 15.1 представлена таблица количества сделок с каким-то товаром и размеры сделок по месяцам. Несколь­ко слов о том, как вычислены значения: «всего» сделок, «всего» продано товара, «в среднем» сделок, «в среднем» размер сделки. Для подсчета общего количества сделок, ячейка «N2», применена функция суммирования =СУММ(В2:М2). Для подсчета среднего количества сде­лок, ячейка «O2», применена функция =СРЗНАЧ(В2:М2).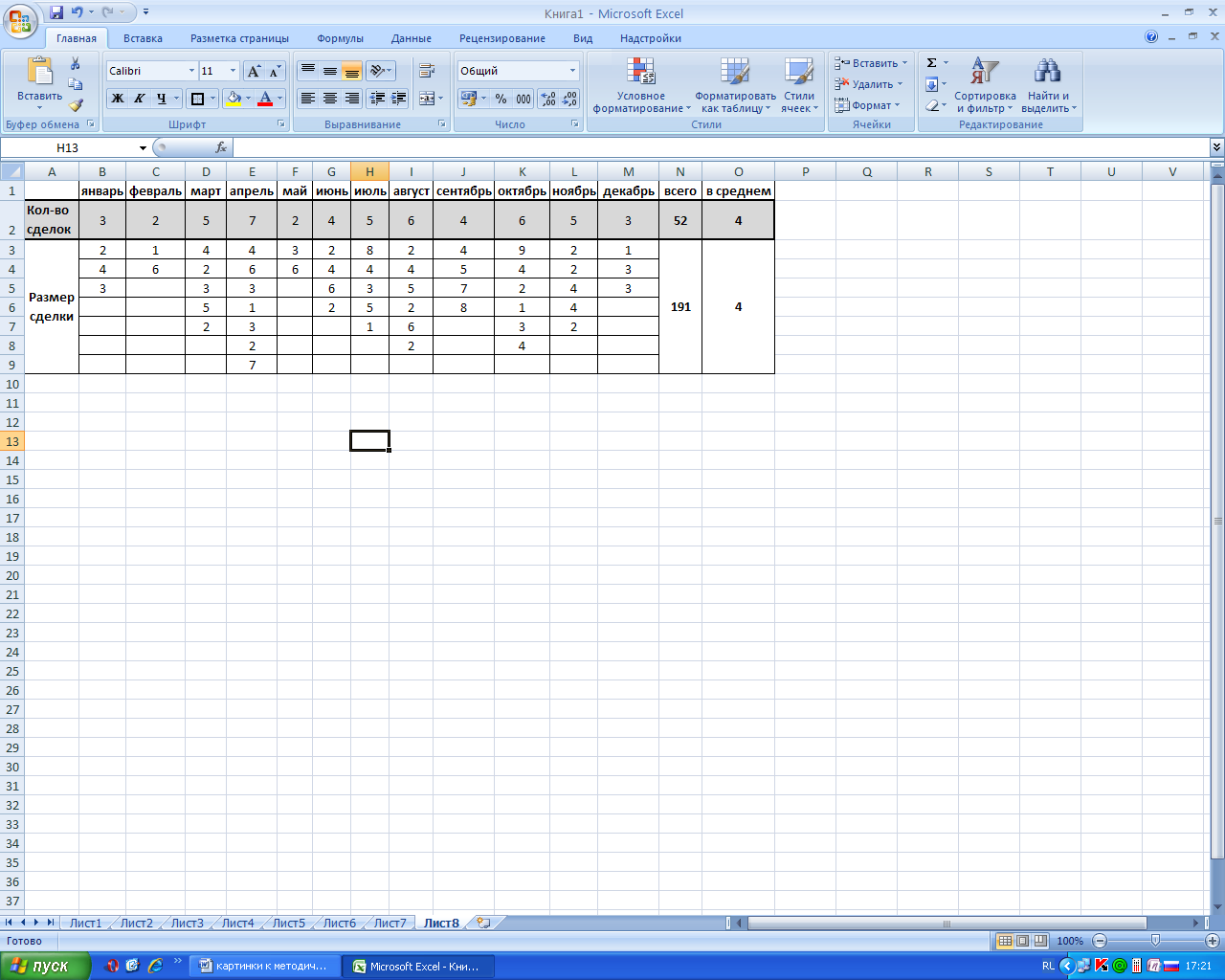



Рис. 15.1. Таблица количества сделок с товаром и размеров сделок по месяцам.

Для подсчета общего количества проданного товара, ячейка «N3», также применена функция суммирования =СУММ(В3:М9). Однако обратите внимания на указан­ный в ней диапазон суммирования. Он имеет вид двумерного массива. Границы диапазона задаются левой верх­ней ячейкой массива — «В3» и правой нижней — «М9». Аналогичным образом рассчитывается и среднее значе­ние размера сделки в ячейке «O3»: =СРЗНАЧ(ВЗ:М9).

Рассчитаем, как часто совершается сделка с тем или иным количеством товара. Иными словами, построим таб­лицу частот размеров сделок. Для этого воспользуемся функцией ЧАСТОТА.

Мастер функции имеет вид, как показано на рис. 15.2. Параметр «Массив_данных» — это набор данных или ди­апазон ячеек, для которых необходимо рассчитать часто­ты. Параметр «Массив_интервалов» — это набор интер­валов или диапазон ячеек с набором интервалов, в которых группируются значения из «Массива данных».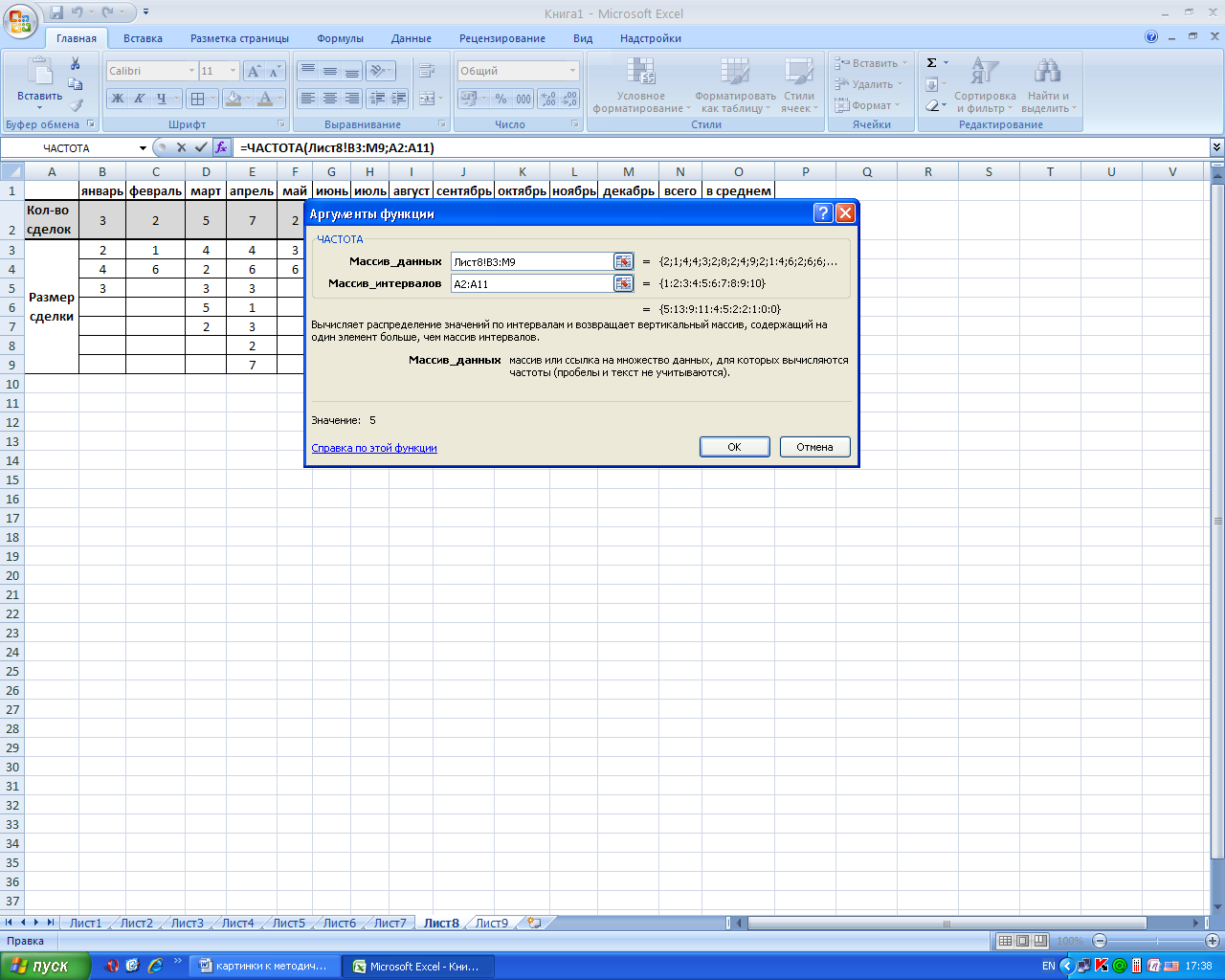



Рис. 15.2. Мастер функции «ЧАСТОТА».

Поясним на примере. Пусть имеется массив данных вида: 1,2,3,4,2,3,2. Если массив интервалов имеет вид: 1,2,3,4, функция вернет значения 1,3,2,1. Этот набор цифр означа­ет, что в массиве данных содержится одна «1», три «2», две «3», одна «4». Соответственно, если массив интервалов бу­дет иметь вид: 2,4, функция сосчитает количество значе­ний, попавших в интервалы 1-2 и 3-4, и вернет значения 4,3. Функция ЧАСТОТА должна вводиться как формула массива. Количество выделенных ячеек для ввода фун­кции должно быть на одну больше, чем количе­ство интервалов в «Двоичном массиве». В «лиш­нюю» ячейку будут попадать частоты для значений, выходящих за верхнюю границу интер­вала. Ячейки должны выделяться вертикально.

На рис. 15.3. представлен результат работы функции ЧАСТОТА. Функция имеет вид

{=ЧАСТОТА(рис.9.1.!В3:М9;А2:А11)}.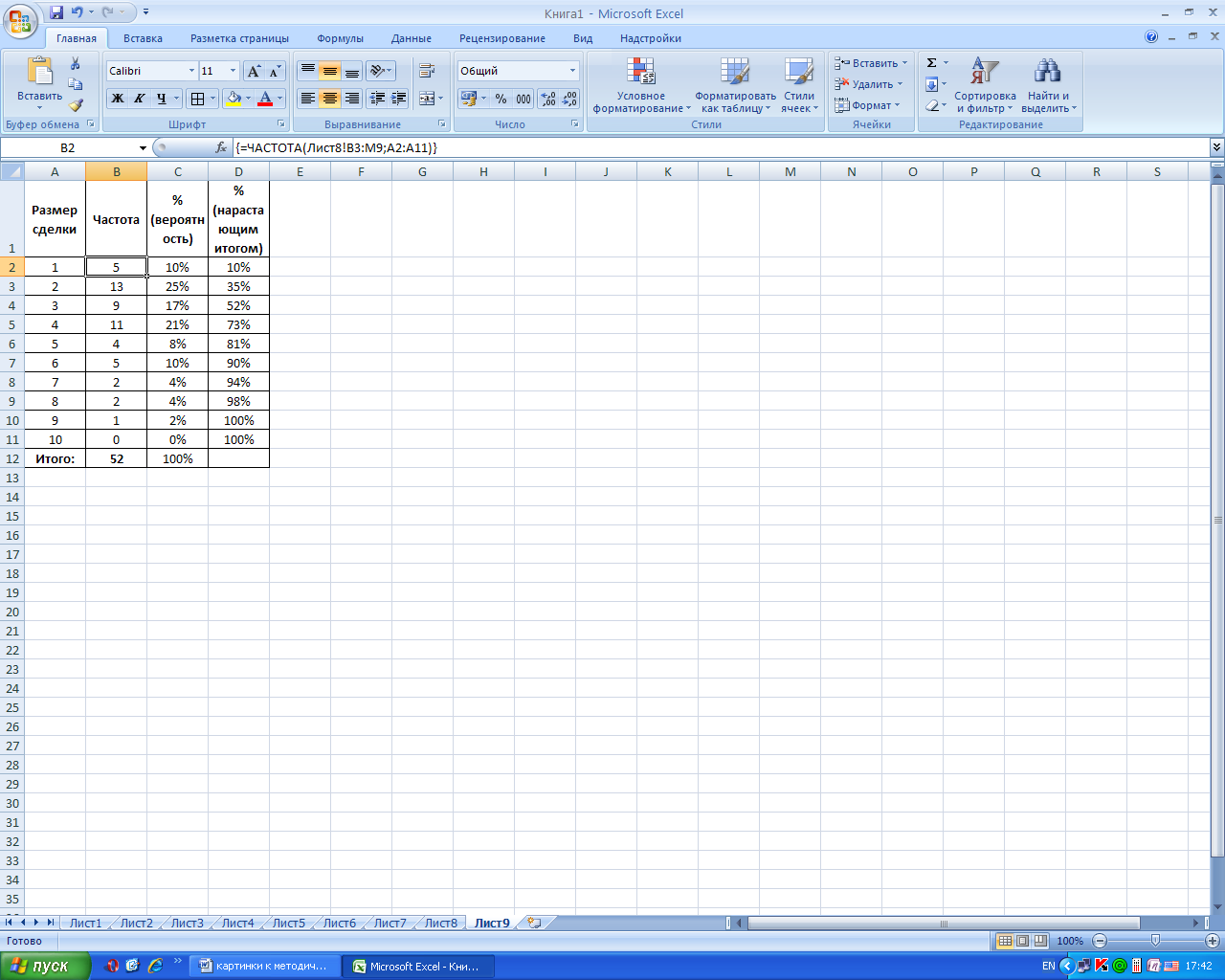



Рис. 15.3. Таблица частот размеров сделок

В качестве массива данных указан двумерный диапазон в таблице 15.1. Как видно из таблицы, наиболее часто встречаются сделки с объемом товара «2» и «4». В столбце С с помощью формулы вида =В2/$В$12 осуществлен расчет вероятности сделки с соответствующим количеством товара. В столбце D вычислены вероятности сделок нарастающим итогом.

Предположим, нужно определить количество товара, которое необходимо положить на склад, чтобы осуще­ствить только одну сделку (однократно продать требуе­мое количество товара клиенту). Из таблицы на рис. 15.3 следует, что если на складе будет присутствовать 2 еди­ницы товара, сделка будет осуществлена в 35 % случаев. В 65 % случаев клиент останется неудовлетворенным. Если на складе будет присутствовать 4 единицы товара, т.е. количество товара, продаваемое в среднем за одну сдел­ку, сделка будет осуществлена в 73% случаев. 100% об­служивание клиента достигается только в случае нали­чия на складе 9 единиц товара.

Уровень обслуживания клиента определяется менедж­ментом компании, на основе маркетингового анализа, фи­нансовых и логистических возможностей. Предположим, выбран уровень обслуживания 90%, т.е. 6 единиц товара на одну сделку. Умножив среднее количество сделок на 6 еди­ниц, получим объем запасов на один месяц.

Как уже было отмечено выше, данный способ опреде­ления объема запаса не является единственным. Вместо среднего количества сделок для расчета запаса может быть применено наиболее вероятное количество сделок, прогнозное количество сделок с учетом сезонности, ли­нейного или экспоненциального тренда.

Кроме функции ЧАСТОТА, полезным может оказать­ся применение функций МОДА, МЕДИАНА, МИН, МАКС. У всех перечисленных функций под скобками указывает­ся диапазон массива с данными для анализа. Можно ука­зать от одного до тридцати диапазонов, разделив их зна­ком «точка с запятой».

Функция МОДА возвращает наиболее вероятное, наи­более часто встречающееся в массиве данных значение. Для таблицы на рис. 15.1 формула будет иметь вид =МОДА(В3:М9) и вернет значение «2».

Функция МЕДИАНА возвращает значение медианы массива данных. Медиана — это число, которое делит область изменения значений в массиве данных на два ин­тервала, попадания в которые имеют равные вероятнос­ти. Для таблицы на рис. 15.1 формула будет иметь вид =МЕДИАНА(ВЗ:М9) и вернет значение «3».

Функция МИН возвращает минимальное значение в мас­сиве данных, а функция МАКС — максимальное. Для таб­лицы на рис. 15.1 формула будут иметь вид =МИН(В3:М9) и =МАКС(ВЗ:М9).