Задачи по логистики. Решение задач с помощью ms excel 46
 Скачать 7.4 Mb. Скачать 7.4 Mb.
|
СодержаниеЛОГИСТИКА ЗАКУПОК 3 1. ОПРЕДЕЛЕНИЕ ПОТРЕБНОСТИ В МАТЕРИАЛЬНЫХ РЕСУРСАХ 3 Наивный прогноз 4 Прогнозирование по средним значениям 4 Прогнозирование по скользящему среднему значению 5 Метод взвешенной скользящей средней 5 Регрессионный анализ 9 СКЛАДСКАЯ ЛОГИСТИКА 15 Определение месторасположения склада 15 Типовые задачи (примеры и задания для самостоятельного решения) 18 Производительность машин 26 ТРАНСПОРТНАЯ ЛОГИСТИКА 30 Транспортная задача 30 Выбор подвижного состава для перевозки продукции 39 Определение оптимального срока замены транспортного средства 43 Решение задач с помощью MS Excel 46 ОБОРАЧИВАЕМОСТЬ ТОВАРНО-МАТЕРИАЛЬНЫХ ЗАПАСОВ 46 ИЗЛИШКИ ТОВАРНЫХ ЗАПАСОВ И УСЛОВНОЕ ФОРМАТИРОВАНИЕ 55 ПЕРЕНОС ДАННЫХ ИЗ НЕСКОЛЬКИХ ТАБЛИЦ-ИСТОЧНИКОВ В ТАБЛИЦУ-ЦЕЛЬ 58 ИНДЕКС СЕЗОННОСТИ И ПРОГНОЗИРОВАНИЕ СБЫТА 61 КРАТКОСРОЧНОЕ ПРОГНОЗИРОВАНИЕ В MICROSOFT EXCEL 64 ОЦЕНКА ПОТРЕБНОСТИ В ЗАПАСАХ ТОВАРОВ НЕРЕГУЛЯРНОГО СПРОСА 68 ВЫЯВЛЕНИЕ КОМПЛЕМЕНТАРНЫХ ТОВАРОВ И ТОВАРОВ СУБСТИТУТОВ 70 Управление запасами с применением анализа АВС и XYZ 73 Решение транспортной задачи в Microsoft Excel с помощью Поиска решения 88 Рисунок 7 92 ЛОГИСТИКА ЗАКУПОК Логистика закупок — это функциональный блок логистики, связанный с управлением материальными потоками в процессе обеспечения предприятия всеми необходимыми ресурсами. Любое предприятие, как производственное, так и торговое, имеет службу, осуществляющую закупку, доставку и временное хранение сырья, полуфабрикатов и товаров народного потребления. Появление термина «закупочная логистика» не случайно. За рубежом сфера деятельности по обеспечению компании (фирмы-производителя или торговой компании) необходимыми видами материальных ресурсов и готовой продукции традиционно называется purchasing (procurement) — закупки (управление закупками, снабжение). Эта же область производственной деятельности в отечественной практике до сих пор называется материально-техническим снабжением (обеспечением), на предприятиях оптовой торговли — товароснабжением. Однако в последние годы эту область стали определять как закупочную логистику, поскольку изменился характер материально-технического обеспечения предприятий: от жестко централизованного, фондируемого снабжения к свободной оптовой торговле ресурсами. Основными задачами, решаемыми закупочной логистикой, являются: определение предмета (структуры) закупок; определение потребности в материальных ресурсах; выбор поставщика; определение объема закупок; определение условий закупок; подготовка и размещение заказа на покупку; контроль выполнения заказа; получение и проверка грузов; обработка счета и оплата; учет поступления материальных ресурсов. 1. ОПРЕДЕЛЕНИЕ ПОТРЕБНОСТИ В МАТЕРИАЛЬНЫХ РЕСУРСАХ Не вызывает сомнения тот факт, что прежде чем осуществить закупку материальных ресурсов, необходимо определить потребность в последних на будущее. Определение потребности в материальных ресурсах основано на прогнозировании их расхода за прошедшие периоды времени. Существует порядка трехсот методов прогнозирования, которые можно разделить на три основные группы: детерминированные; стохастические (вероятностные); эвристические. Прогнозирование обычно основано на использовании статистического материала (исторических данных) о расходовании материальных ресурсов за определенный промежуток времени. Считается, что при наличии статистических данных за три периода можно сделать прогноз на полтора периода вперед. Следует помнить, что материальные ресурсы могут характеризоваться как относительно равномерным спросом, так и иметь резко выраженные сезонные «сгущения» или «разряжения» (например, потребность в новогодних елках). Относительно равномерный спрос характерен для регулярно потребляемых материальных ресурсов, не имеющих сезонных колебаний. Если потребность в материальных ресурсах характеризуется относительно равномерными рядами отгрузок, можно использовать следующие методы прогнозирования: наивный прогноз; группу методов прогнозирования по среднему значению (простой средней, скользящей средней, взвешенной скользящей средней); метод регрессионного анализа. Наивный прогноз Наивный прогноз является самой простой методикой прогнозирования. Он основывается на предположении о том, на сколько прогнозируемое потребление будет соответствовать потреблению в предшествующем периоде. Достоинством наивного прогноза является отсутствие необходимости в накоплении статистических данных. Недостаток — вероятная низкая точность прогноза. Однако при прогнозировании спроса, например, на хлеб или молочные продукты, он вполне оправдан. Так, специалист по закупкам должен быть осведомлен о датах начала-окончания православных постов и иных факторах, оказывающих влияние на изменение потребности в этих продуктах у населения. Прогнозирование по средним значениям В случае если временной ряд имеет интервал наблюдений в один месяц, повысить точность наивного прогноза позволяет метод прогнозирования по простой средней величине потребления с учетом количества рабочих дней в месяце. Среднее дневное потребление Рдн рассчитывается по формуле Рдн = Рмес : ДРмес, (1) гдеРмес — объем потребления материального ресурса за предыдущий месяц, ед.; ДРмес – дни работы в предыдущем месяце. Прогноз потребления на следующий месяц рассчитывается по формуле Рj = Рдн : ДРмесj, (2) где Pj — прогнозируемый объем потребления материального ресурса в j-м месяце, ед.; ДРмесj – дни работы в j-м месяце. Прогнозирование по скользящему среднему значению Еще один метод прогнозирования по средним значениям — это прогноз на основе скользящего среднего значения потребления материального ресурса. При составлении прогноза этим методом используется значение средней арифметической величины потребления за последние периоды наблюдений. Скользящая средняя дневного потребления рассчитывается по формуле 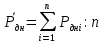 (3) (3)где 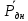 — прогнозируемый объем дневного потребления материального ресурса в j-м периоде времени, ед.; — прогнозируемый объем дневного потребления материального ресурса в j-м периоде времени, ед.; i — индекс предыдущего периода времени; 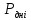 — объем дневного потребления в i-м предыдущем периоде времени; — объем дневного потребления в i-м предыдущем периоде времени; n — количество периодов, используемых в расчете скользящей средней. Прогноз потребления на месяц рассчитывается по формуле 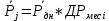 (4) (4)где 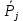 — прогнозируемый объем потребления материального ресурса в j-м месяце, ед.; — прогнозируемый объем потребления материального ресурса в j-м месяце, ед.;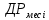 - дни работы в j-м месяце. - дни работы в j-м месяце.Для составления прогноза на основе скользящего среднего значения потребления материального ресурса требуется определить количество периодов наблюдений, которые будут использоваться при расчете. При этом необходимо учитывать особенности имеющегося временного ряда. Чем большее количество точек наблюдений берется в расчет, тем скользящая средняя менее чувствительна к изменениям значений потребления в прошлые периоды. Преимущество метода прогнозирования по скользящей средней заключается в его простоте. Основным же недостатком является то, что значимость потребления в прошлые периоды при прогнозировании будущей потребности одинакова, что редко встречается на практике. Метод взвешенной скользящей средней Для учета важности отдельных периодов наблюдений используют метод взвешенной скользящей средней. В этом методе каждому используемому в расчете скользящей средней периоду присваивается коэффициент, отражающий значимость влияния этого периода на прогнозное значение потребления. Значимость более поздних периодов должна быть выше, чем значимость более ранних периодов. Например, из шести периодов расчета скользящей средней последнему может быть присвоен удельный вес 5, предыдущему — 4, далее 3; 2 и 1. В общем виде взвешенная скользящая средняя рассчитывается следующим образом: 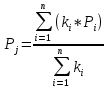 (5) (5)где 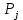 - прогнозируемый объем потребления материального ресурса в j-м периоде времени, ед.; - прогнозируемый объем потребления материального ресурса в j-м периоде времени, ед.;i - индекс предыдущего периода времени; 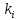 - коэффициент значимостиi-го периода; - коэффициент значимостиi-го периода;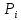 - объем потребления в i-м предыдущем периоде времени; - объем потребления в i-м предыдущем периоде времени;n - количество периодов, используемых в расчете взвешенной скользящей средней. Пример 1. Прогнозирование потребности в материальных ресурсах. Исходные данные для определения потребности в материальных ресурсах (MP), результаты наивного прогноза и результаты расчетов прогнозирования на основе среднего потребления приведены в табл. 1. Прогнозирование по скользящей средней. В рассматриваемом примере колебания потребления MP в течение первой половины года не длятся более двух месяцев. Во второй половине года имеются более длительные тенденции (до четырех месяцев в конце года). Игнорируя пока характер сезонных колебаний и тенденции рассматриваемого примера, выберем в качестве интервала расчета скользящей средней два месяца. Результат расчета прогноза по скользящей средней с учетом количества рабочих дней в месяце приведен в табл. 2. Таблица 1 Исходные данные для определения потребности в MP и результаты наивного прогноза и по средним значениям
Прогнозирование по взвешенной скользящей средней. Для данных в табл. 2 выберем коэффициенты значимости прошлых периодов при прогнозировании потребности будущего периода. Для последнего периода коэффициент значимости принимается равным 5, для предпоследнего — 1. Расчет взвешенной скользящей средней приведен в табл. 2. Для расчета прогноза среднедневного потребления MP (см. столбец 7 табл. 2), например в марте, требуется статистика фактических среднедневных отгрузок (столбец 4 табл. 2) за январь и февраль: 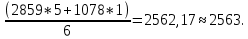 Округление потребления производится в большую сторону для гарантии обеспечения материальным ресурсом. Для получения прогноза месячной потребности в MP в марте (столбец 8 табл. 2) необходимо прогноз среднесуточной потребности в марте умножить на количество рабочих дней в этом месяце. Таблица 2 Расчет прогнозного значения потребления MP по скользящей средней и по взвешенной скользящей средней
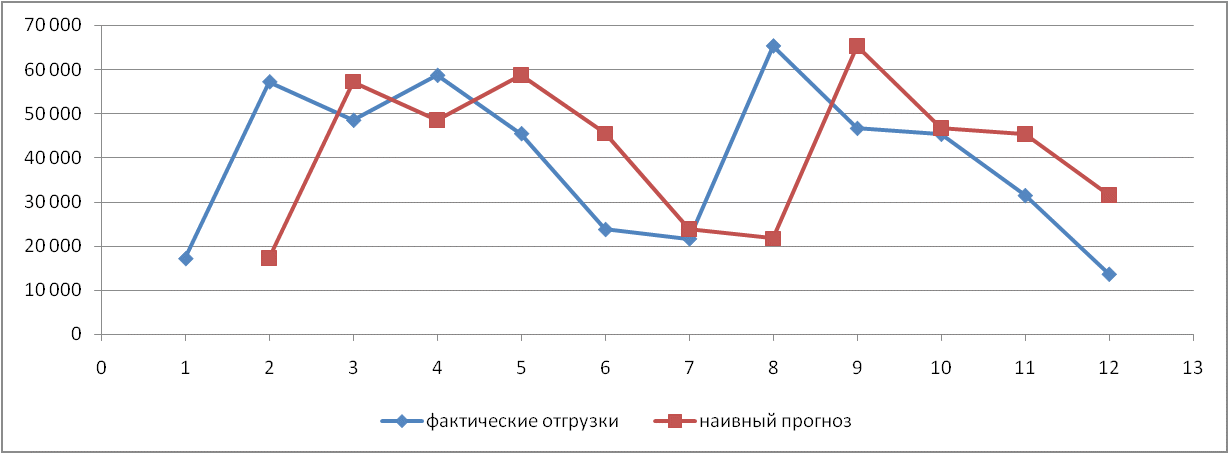 Рис. 1. Результаты наивного прогноза потребности в MP 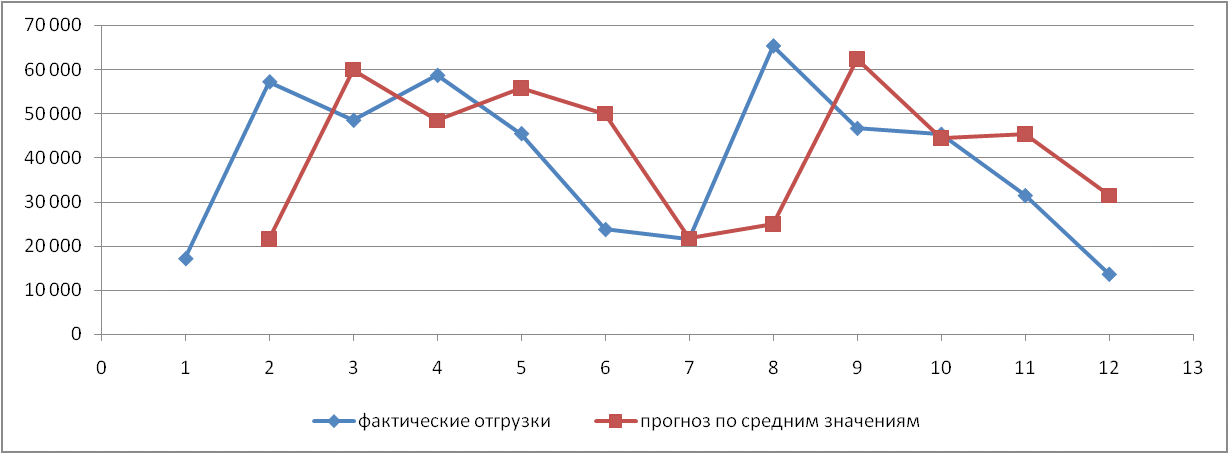 Рис. 2. Результаты прогноза на основе среднего потребления 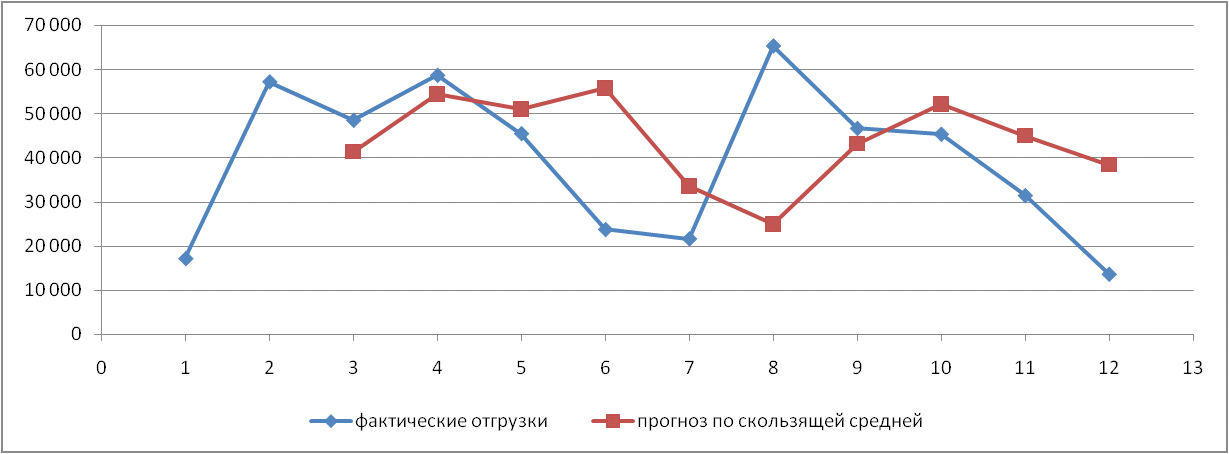 Рис. 3. Результаты прогноза по скользящей средней 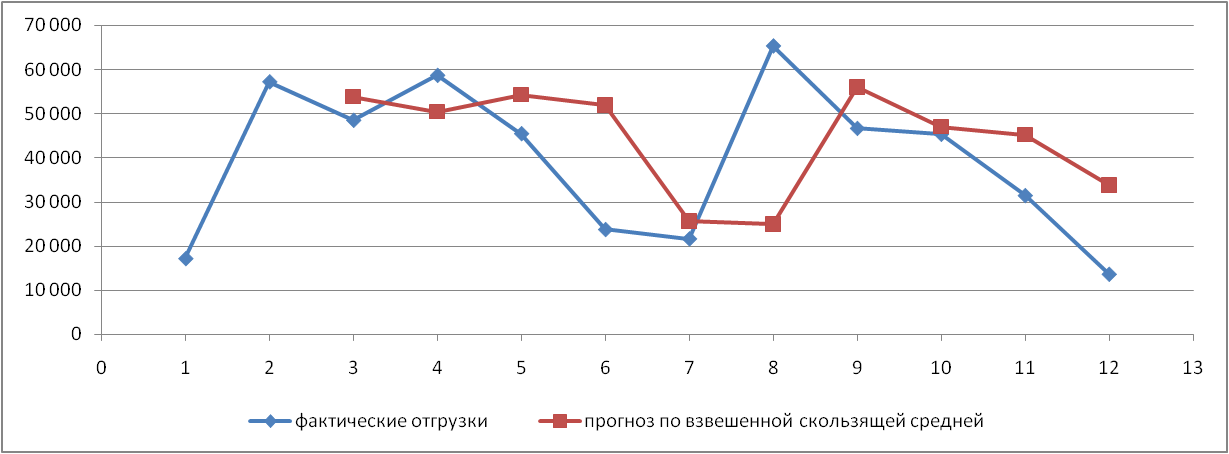 Рис. 4. Результаты прогноза по взвешенной скользящей средней Как видно из примера, если потребление характеризуется колебаниями (сезонными или обусловленными какими-либо иными тенденциями), то ни один из видов прогноза не является в достаточной степени достоверным (рис. 1—4). В этом случае целесообразно провести научное исследование потребления MP и, в частности, воспользоваться методикой регрессионного анализа. Регрессионный анализ Под регрессионным анализом понимают группу методов, позволяющих с достаточной степенью точности выявлять закономерности изменения случайных величин, устанавливать вид этих зависимостей. В данном случае под случайной величиной понимается расходование материальных ресурсов (фактические отгрузки), которое зависит от периодов потребления (года, месяца, дня и т.д.). Для прогнозирования материалопотока и товарооборота склада необходимо подобрать наиболее подходящее из известных математических уравнений функций (прямую, гиперболу, параболу и т. д.). Эти уравнения определяются на основании графиков, которые строятся по отчетным данным (динамическим рядам). Рассмотрим эти уравнения. Уравнение прямой имеет следующий вид: ух = а +b* х, (6) где ух — результативный признак; х — период времени; а иb — параметры прямой. Нахождение параметров а иb производится на основе выравнивания по способу наименьших квадратов, которые приводят к системе двух линейных уравнений с двумя неизвестными: 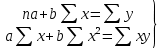 (7) (7)Решая это уравнение, находим: 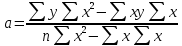 ; ;  (7a) (7a)В целях облегчения нахождения параметров а иb систему можно упростить. Для этого отсчет времени следует вести так, чтобы сумма показателей времени ряда была равна нулю. Такая условность вполне допустима ввиду того, что начало выбирается произвольно. Чтобы 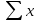 равнялась нулю, в рядах с нечетным числом членов центральный член принимается за нуль, а члены, идущие от центра (в столбце) вверх, получают номера от -1, -2, -3 — со знаком минус, а вниз — +1, +2, +3 — со знаком плюс. Например, ряд составляет 7 членов равнялась нулю, в рядах с нечетным числом членов центральный член принимается за нуль, а члены, идущие от центра (в столбце) вверх, получают номера от -1, -2, -3 — со знаком минус, а вниз — +1, +2, +3 — со знаком плюс. Например, ряд составляет 7 членов 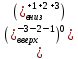 . Если число членов ряда четное (например, 6), рекомендуется занумеровать члены верхней половины ряда (от середины) числами -1, -3, -5 и т. д., члены нижней половины (от середины) — +1, +3, +5 и т. д. В обоих случаях . Если число членов ряда четное (например, 6), рекомендуется занумеровать члены верхней половины ряда (от середины) числами -1, -3, -5 и т. д., члены нижней половины (от середины) — +1, +3, +5 и т. д. В обоих случаях 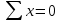 . .Если члены динамического ряда получили такую нумерацию, что их сумма оказывается равной нулю, то система уравнений принимает вид 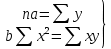 Отсюда Отсюда  ; ; 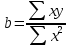 (8) (8)Из приведенных формул видно, что для нахождения параметров уравнения прямой необходимо знать величины 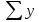 , , 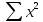 , , 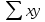 . .Если уровни динамического ряда обнаруживают тенденцию роста по геометрической прогрессии, т. е. прирастают на одинаковое число процентов, выравнивание такого ряда следует проводить по показательной кривой: ух = abx. В этом уравнении х — рассматриваемый период, а — начальный уровень ряда (при х = 0),b — темп роста за единицу времени. Техника выравнивания по показательной кривой аналогична технике выравнивания по прямой. Кроме выравнивания и прогнозирования по прямой и показательной кривой, на практике часто используются и другие функции. Например, уравнение параболы второго порядка: yx = a + bx + cx2, (9) где а, b, с — параметры, которые находятся из системы нормальных уравнений. Сама система уравнений, получаемая по способу наименьших квадратов, следующая: 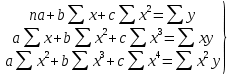 (10) (10)Обозначим время таким образом, что 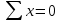 . В этом случае нулю будет равно и . В этом случае нулю будет равно и 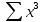 (как всякая сумма нечетных степеней х). В силу сказанного система нормальных уравнений примет вид: (как всякая сумма нечетных степеней х). В силу сказанного система нормальных уравнений примет вид: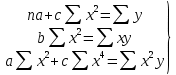 . (11) . (11)Во втором уравнении: 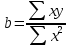 ; (12) ; (12)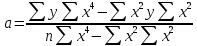 ; ; 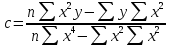 . (13) . (13)В расчетах также динамический ряд может быть описан уравнением гиперболы: yx = a + b / x. (14) Для гиперболической зависимости способ наименьших квадратов дает такую систему нормальных уравнений: 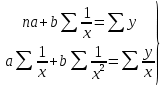 . (15) . (15)Решая это уравнение способом определителей, находим: 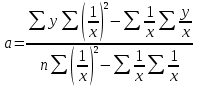 ; ; 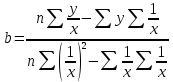 (16) (16)Пример 2. За период с 2004 по 2010 г. известен динамический ряд товарооборота регионального склада (табл. 3). Сделайте прогноз товарооборота на 2013 г. Таблица 3 Товарооборот за период 2004—2010 гг.
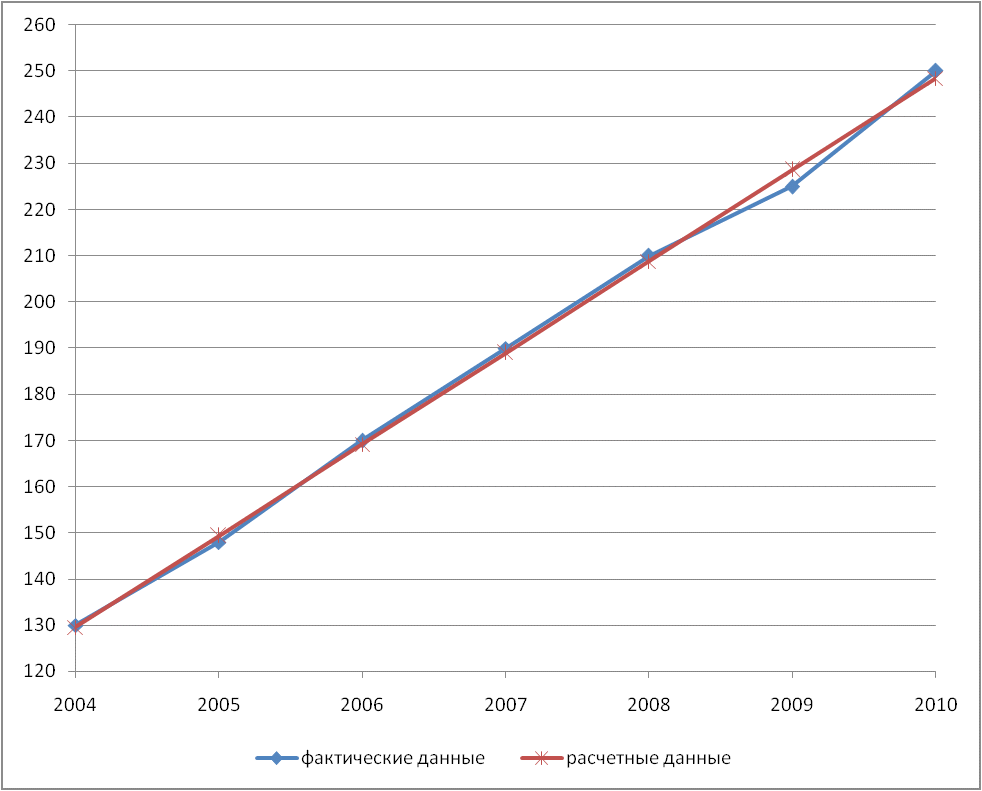 Рис. 5. Динамика изменения товарооборота за период 2004—2010 гг.: Решение. По данным табл. 3 строим график (рис. 5) динамики изменения товарооборота за период 2004—2010 гг. Из этого графика видна тенденция изменения товарооборота. Она идет по прямой линии. Поэтому связь между указанными признаками может быть описана уравнением: ух = а +b* х, где ух — товарооборот регионального склада в условных единицах; х — рассматриваемый период; а иb — параметры (табл. 4). Найденные значения подставим в формулы (8), получим параметры а иb: 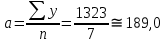 ; ; 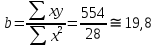 . .Уравнение нашей прямой будет: ух = 189 + 19,8х. Таблица 4 Расчет параметров уравнения прямой для прогнозирования товарооборота в 2013 г.
Подсчитаем теоретические уровни ряда для каждого года (гр. 6, табл. 4). Сопоставленные графы 2 и 6 по каждому году показывают весьма незначительные отклонения расчетных уровней от фактических, что подтверждает правильность выбора математического уравнения. Для прогнозирования товарооборота необходимо продолжить графу 3 (рассматриваемый период) числами, следующими за указанным числом. В нашем случае это 3, далее рассматриваемый период будет 4, 5, 6 и т. д. На 2013 г. х = 6, тогда у2013 = 189 + 19,8 * 6 = 307,8. Пример 3. За период 2005—2010 гг. известен динамический ряд объема перевозок грузов с регионального склада (табл. 5). Сделайте прогноз перевозок в 2013 г. Исчислим параметры а, b, с по данным табл. 6 и формулам (12), (13). Таблица 5 Объем перевозок за период 2005—2010 гг. (тыс. т)
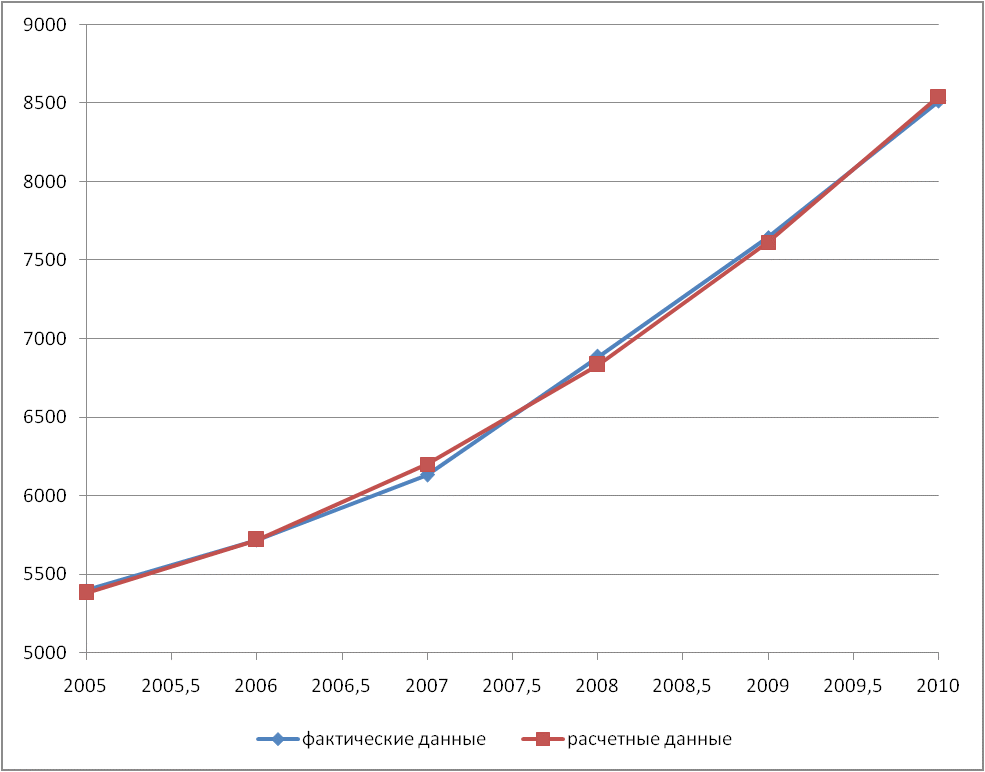 Рис. 6. Динамика изменения объема перевозок за период 2005—2010 гг.: 1 — фактические данные;2 — расчетные данные Таблица 6 Расчет параметров уравнения параболы для выравнивания и прогнозирования объема перевозок с регионального склада
Отсюда: а = (40 298 * 1,414 - 481 202 * 70)/(6 * 1414 - 702) 6500,3; b= 22 140/70 316,3; с = (6 * 481 202 – 70*40*40 298)/(6 * 1414 - 702) 18,51. Таким образом, уравнение параболы в нашем примере имеет вид: ух = 6500,3 + 316,3х + 18,51х2. Подставив в эту формулу конкретные значения х, находим значения ух для всех членов динамического ряда (гр. 8, табл. 6). Сопоставленные графы 2 и 8 показывают незначительные отклонения теоретических уровней от эмпирических, что свидетельствует о правильности выбора уравнения кривой. В 2013 г. объем перевозки грузов с регионального склада составит: у2013 = 6500,3 + 316,3 * 11 + 18,51 * 11 = 12 219,31. Задачи для самостоятельного решения Задача 1. Сделайте прогноз товарооборота на 2011 г. (данные в табл. 7). Таблица 7 Исходные данные для расчета
Задача 2. В таблице 8 приведены статистические данные расходования материального ресурса за последние 6 месяцев. Необходимо сделать прогноз расходования МР в 9 месяце. Таблица 8 Исходные данные для расчета
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
