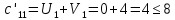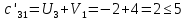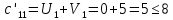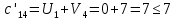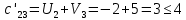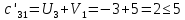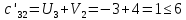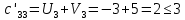Задачи по логистики. Решение задач с помощью ms excel 46
 Скачать 7.4 Mb. Скачать 7.4 Mb.
|
ТРАНСПОРТНАЯ ЛОГИСТИКАТранспортная задача Постановка задачи Тип транспортной задачи Модель транспортной задачи Математическая формулировка задачи Решение транспортной задачи Решение транспортной задачи в Microsoft Excel с помощью Поиска решения 6.1.Технология работы 6.2.Решение открытой транспортной задачи 1. Постановка задачи Задача ставится следующим образом. Найти объем перевозок для каждой пары «поставщик-потребитель» так, чтобы: мощности всех поставщиков были реализованы; спросы всех потребителей были удовлетворены; суммарные затраты на перевозку были минимальными. 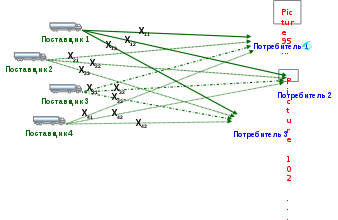 Рисунок 1 Таблица 1
аi – объем продукции, поставляемый i-ым производителем (поставщиком) bj – объем продукции, получаемый j-м потребителем cij – стоимость поставки единицы продукции от i-го производителя к j-му потребителю (удельная стоимость перевозок) xij – объем поставляемой продукции от i-го производителя к j-му потребителю (план перевозок) 2. Тип транспортной задачи Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения: 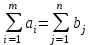 Если такого равенства нет (потребности выше запасов или наоборот), задачу называют открытой, то есть: 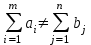 3. Модель транспортной задачи Все грузы должны быть отправлены:  Все потребители должны быть обеспечены грузами в плановом объеме: 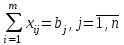 С 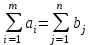 уммарные объемы отправления должны равняться суммарным объемам назначения (уравнение баланса): уммарные объемы отправления должны равняться суммарным объемам назначения (уравнение баланса):Должны выполняться условия неотрицательности переменных: 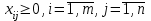 Целевая функция - транспортные издержки должны быть минимальны:  4. Математическая формулировка задачи На множестве неотрицательных решений системы ограничений найти такое решение, при котором целевая функция принимает минимальное значение. 5. Решение транспортной задачи Транспортная задача решается методом потенциалов Этапы: Разработка начального плана Расчет потенциалов Проверка плана на оптимальность Поиск максимального звена неоптимальности (если условие третьего пункта не достигнуто) Составление контура перераспределения ресурсов (цикла) Определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру Получение нового плана. Описанная процедура повторяется несколько раз (итераций), пока не будет найдено оптимальное решение. Вычислительный алгоритм для каждой итерации не меняется. Пример. На 3 базах а1, а2, а3 имеется однородный товар количеством 200 т, 110 т и 90 т, соответственно. Этот товар нужно отгрузить магазинам b1, b2, b3 и b4, потребность которых составляет 50 т, 100 т, 150 т и 100 т, соответственно. Транспортные издержки cij – в тыс. руб. на тонну. Матрица тарифа 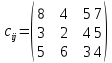 Составить план отгрузки товара, чтобы транспортные расходы были минимальными. Решение: 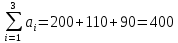 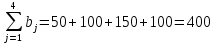 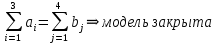 Начальный план можно составить несколькими методами. Рассмотрим метод «северо-западного угла», метод двойного предпочтения и метод аппроксимации (Фогеля). 1. Метод «северо-западного угла». Загрузка клеток начинается с верхней левой клетки и продолжается вниз и вправо. При этом клетки загружаются максимально возможным образом. По указанному правилу загружаем первую клетку из условия 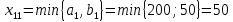 Таким образом, первый пункт назначения загружен, а первый пункт отправления имеет остатки груза 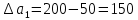 , которые и распределяем на второй пункт назначения: , которые и распределяем на второй пункт назначения: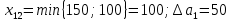 Продолжая аналогичным образом, получаем: 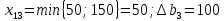 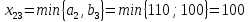 Результаты расчета начального плана представлены в табл.2. Таблица 2
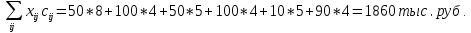 Недостатком данного метода является то, что он не учитывает значения элементов cij матрицы транспортных расходов, в результате чего полученное этим методом начальное распределение (начальный опорный план перевозок) может быть достаточно далеко от оптимального. 2. Метод двойного предпочтения. Отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наименьшими стоимостями. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок. Вычеркивание строк и столбцов при заполнении клеток проводится по описанным выше правилам. Пример начального распределения методом наименьших стоимостей для тех же исходных данных, что и ранее, представлен в табл. 3. Таблица 3.
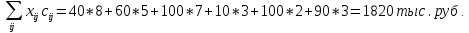 Этот результат лишь незначительно лучше начального плана, составленного методом «северо-западного угла». 3. Метод аппроксимации (Фогеля). При определении начального плана транспортной задачи методом аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Для решения внизу матрицы вводят дополнительную строку, в которую заносят разности между двумя минимальными значениями стоимости перевозок в каждом j-м столбце. С правой стороны матрицы вводят дополнительный столбец, в который записывают разности между двумя наименьшими значениями стоимости перевозок по каждой i-й строке. Таблица 4
Среди всех разностей, вписанных в дополнительной строке и дополнительном столбце, выбирают наибольшую. В нашем примере два значения имеют одинаковую наибольшую разность 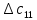 и и 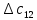 ; в одном случае необходимо загрузить клетку (2;1), в другом - (2;2). Поскольку оба варианта находятся на одной строке, выбирают тот из них, который с максимальным значением стоимости в своем столбце имеет наибольшее значение: ; в одном случае необходимо загрузить клетку (2;1), в другом - (2;2). Поскольку оба варианта находятся на одной строке, выбирают тот из них, который с максимальным значением стоимости в своем столбце имеет наибольшее значение: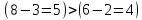 Значит, надо остановиться на клетке (2;1). Загрузка осуществляется по максимуму. Столбец с номером j = 1 полностью загружен и из дальнейшего рассмотрения исключается (вычеркивается). По второй строке имеются остатки: 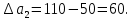 Для оставшихся в рассмотрении вариантов вновь добавляем дополнительные строку и столбец, в которые выписываем разность между наименьшими стоимостями. На этот раз также два значения 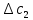 оказались одинаковыми, однако оба раза они получены с участием одного вычитаемого оказались одинаковыми, однако оба раза они получены с участием одного вычитаемого 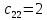 , что указывает на необходимость загрузки клетки (2;2): , что указывает на необходимость загрузки клетки (2;2):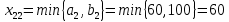 Проставляем загрузку 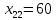 в клетку (2;2), исключаем из рассмотрения строку с номером i = 2 и переходим к следующей итерации. Среди разностей в клетку (2;2), исключаем из рассмотрения строку с номером i = 2 и переходим к следующей итерации. Среди разностей 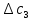 наибольшая получена при вычитании наибольшая получена при вычитании 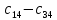 , следовательно, загружаем клетку (3;4): , следовательно, загружаем клетку (3;4):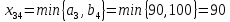 Так как после итерации остался лишь один пункт отправления а1 = 200, то варианты распределения этого груза по пунктам назначения однозначны: 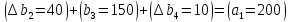 Полученные значения проставляем в соответствующие клетки таблицы, и расчет закончен. Подсчитываем функцию цели: 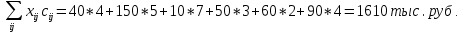 Расчет потенциалов выполняют по загруженным клеткам ( 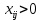 ), используя формулу ), используя формулу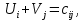 Где 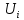 - потенциал i-й строки - потенциал i-й строки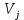 - потенциал j-го столбца - потенциал j-го столбцаВозьмем для дальнейшего расчета начальный план, полученный методом «северо-западного угла». Пусть 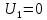 . Получим: . Получим: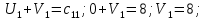 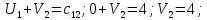 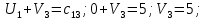 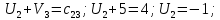 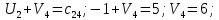 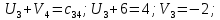 Результаты расчетов потенциалов представлены в табл.5. Таблица 5
Проверка плана на оптимальность. План считается оптимальным, если для всех незагруженных клеток выполняется условие 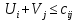 . .При этом количество загруженных клеток равно 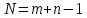 Где m – количество строк, n – количество столбцов. Если количество загруженных клеток меньше чем 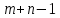 , то в этом случае вводятся условно загруженные клетки «значащие ноль». , то в этом случае вводятся условно загруженные клетки «значащие ноль».По табл.5 осуществляем проверку начального плана на оптимальность:
Поиск максимального звена неоптимальности. Оценивая разности 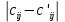 , выберем ту из них, модуль которой будет наибольшим. В нашем примере это 4, следовательно, именно клетка (2;1) должна из незагруженной клетки перейти в загружаемую. В табл. 5 клетку (2;1) помечаем знаком (+) и пересчитаем ее по циклу. , выберем ту из них, модуль которой будет наибольшим. В нашем примере это 4, следовательно, именно клетка (2;1) должна из незагруженной клетки перейти в загружаемую. В табл. 5 клетку (2;1) помечаем знаком (+) и пересчитаем ее по циклу.Составление контура перераспределения ресурсов (цикла). Циклом в таблице транспортной задачи называется замкнутый многоугольник, сторонами которого являются горизонтальные и вертикальные отрезки. Одна его вершина совпадает с загружаемой клеткой, а все остальные вершины находятся в загруженных клетках. При этом загружаемая клетка имеет знак (+), а остальные вершины имеют чередующиеся знаки. Определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру. Из чисел, записанных в клетках цикла со знаком (-) выберем минимальное. 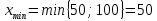 В клетках с (-) вычитаем 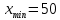 , а в клетках с (+) прибавляем , а в клетках с (+) прибавляем 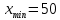 В процессе перераспределения ресурсов может произойти полная разгрузка двух и более клеток. В этом случае следует считать незагруженной только одну из них, а остальные, проставив нулевой ресурс 0, считать условно загруженными. Таблица 6
Получение нового плана (итерации) осуществляется в том же порядке, который был рассмотрен. До тех пор, пока не будет найдено оптимальное решение, удовлетворяющее неравенству: 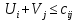 . .По результатам первой итерации имеем: 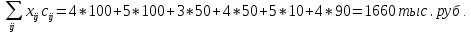 Ниже приведен план второй итерации. Расчет потенциалов Проверка плана на оптимальность
Поиск максимального звена неоптимальности (если условие третьего пункта не достигнуто) (клетка (2;2)) Составление контура (цикла) перераспределения ресурсов Определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру Таблица 7
В соответствии с перераспределением ресурсов по контуру (циклу) получаем табл.7, для которой вновь рассчитываем потенциалы и проверяем план на оптимальность.
Таким образом, условие 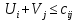 выполняется, и план, представленный в табл.7, является оптимальным. выполняется, и план, представленный в табл.7, является оптимальным.Транспортные издержки по оптимальному плану: 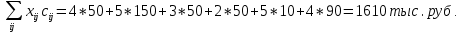 При решении транспортных задач необходимо знать ряд особенностей. Важнейшим инструментом получения улучшенного решения является перераспределение ресурсов по контуру (циклу). Помимо простых контуров, которые встречались в рассмотренной задаче, на рис. 2 приведен пример более сложных контуров. Рисунок 2 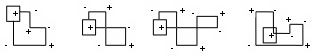 Если при решении не выполняется условие 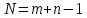 , то вырожденность задачи можно устранить следующими приемами: , то вырожденность задачи можно устранить следующими приемами:Поменять местами столбцы; Ввести фиктивную клетку со «значащим» нулем (сделать условную загрузку клетки) Маршрутизация автомобильных перевозок | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

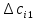
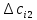
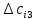
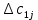
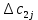
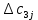
 0
0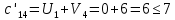
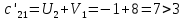
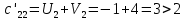
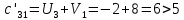
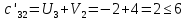
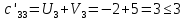
 00
00