Решение задач теории игр. Доминирующие стратегии.. Решение задач теории игр. Доминирующие стратегии
 Скачать 135.29 Kb. Скачать 135.29 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ ГОМЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ П. О. СУХОГО Факультет автоматизированных и информационных систем Кафедра «Информационные технологии» ЛАБОРАТОРНАЯ РАБОТА №2 по дисциплине: «Теория игр» на тему: «Решение задач теории игр. Доминирующие стратегии.» Выполнил: студент гр. ИТИ-21 Принял: преподаватель-стажёр Гомель 2022 Цель работы: получить практические навыки решения задач теории матричных игр. Задания: Решить задачи теории матричных игр (по своему варианту – см. Рисунок 1) и сделать выводы об оптимальных стратегиях для каждой из задач. 1.Решить в смешанных стратегиях матричную игру, сведя ее к задаче линейного программирования (ЗЛП). Полученную ЗЛП для первого игрока решить симплекс методом. 2. Преобразовать задачу таким образом, чтобы появилась доминирующая стратегия. Полученную ЗЛП решить средствами пакетов Mathcad или MS Excel. 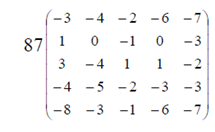 Рисунок 1 – Вариант задания Ход работы: Задание 1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I. Платёжная матрица для задания 1 представлена на рисунке 2. 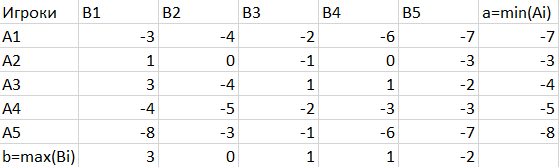 Рисунок 2 – Платёжная матрица для задания 1 Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -3, которая указывает на максимальную чистую стратегию A2. Верхняя цена игры b = min(bi) = -2. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -3 ≤ y ≤ -2. Находим решение игры в смешанных стратегиях. В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (8). Платёжная матрица с положительными элементами представлена на рисунке 3. 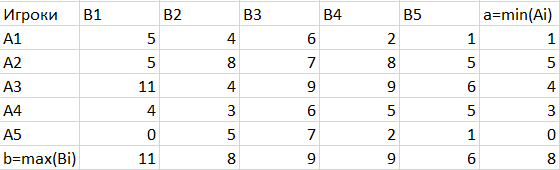 Рисунок 3 – Платёжная матрица с положительными элементами Параметры окна поиск решения представлены на рисунке 4. 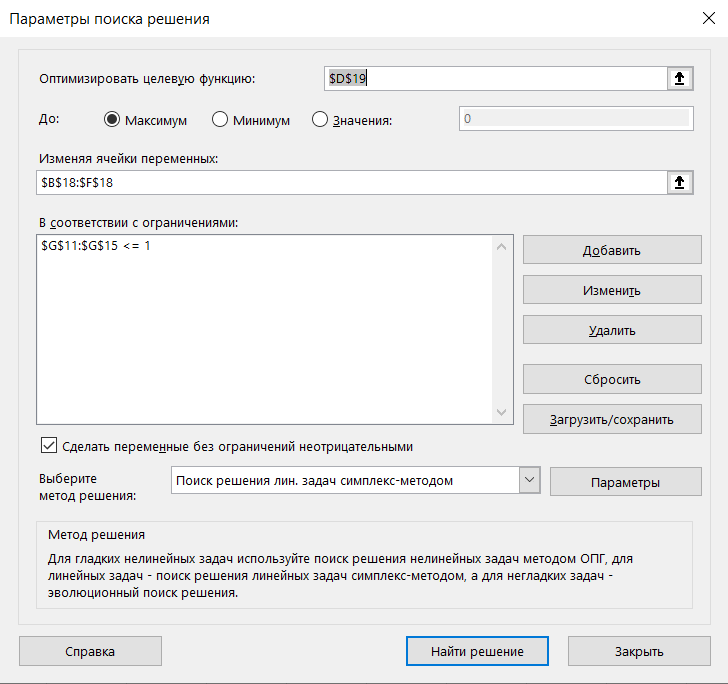 Рисунок 4 – Параметры окна поиск решения Результат поиска решения для матричной игры симпликс-методом представлен на рисунке 5. 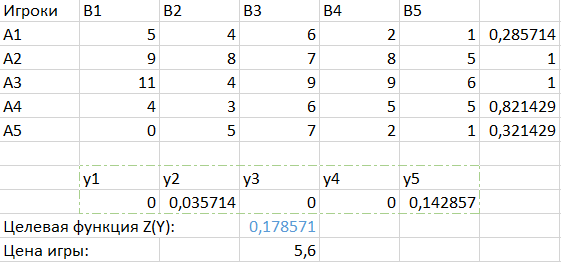 Рисунок 5 – Результат поиска решения для матричной игры симпликс-методом Задание 2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы. Стратегия A2 доминирует над стратегией A1 (все элементы строки 2 больше или равны значениям 1-ой строки), следовательно, исключаем 1-ую строку матрицы. Вероятность p1 = 0. Стратегия A2 доминирует над стратегией A4 (все элементы строки 2 больше или равны значениям 4-ой строки), следовательно, исключаем 4-ую строку матрицы. Вероятность p4 = 0. Стратегия A2 доминирует над стратегией A5 (все элементы строки 2 больше или равны значениям 5-ой строки), следовательно, исключаем 5-ую строку матрицы. Вероятность p5 = 0. Усеченная матрица представлена на рисунке 6.  Рисунок 6 – Усеченная матрица С позиции проигрышей игрока В стратегия B2 доминирует над стратегией B1 (все элементы столбца 2 меньше элементов столбца 1), следовательно, исключаем 1-й столбец матрицы. Вероятность q1 = 0. С позиции проигрышей игрока В стратегия B2 доминирует над стратегией B4 (все элементы столбца 2 меньше элементов столбца 4), следовательно, исключаем 4-й столбец матрицы. Вероятность q4 = 0. С позиции проигрышей игрока В стратегия B5 доминирует над стратегией B3 (все элементы столбца 5 меньше элементов столбца 3), следовательно, исключаем 3-й столбец матрицы. Вероятность q3 = 0. Конечная матрица представлена на рисунке 7. Рисунок 7 – Конечная матрица Параметры окна поиск решения для новой матрицы представлены на рисунке 8. 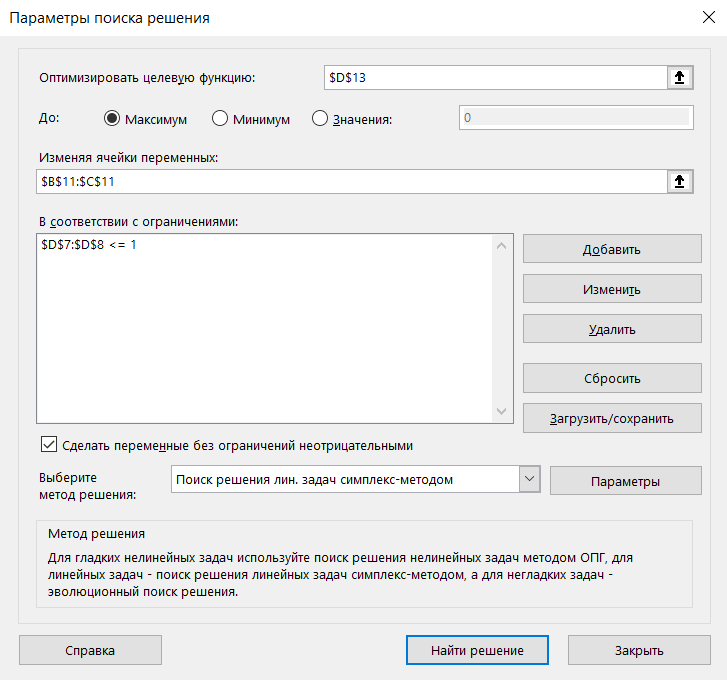 Рисунок 8 – Параметры окна поиск решения Результат поиска решения для матричной игры представлен на рисунке 9. 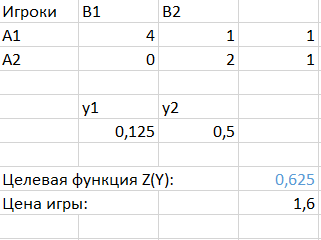 Рисунок 9 – Результат поиска решения Вывод: в ходе выполнения лабораторной работы были получены практические навыки по составлению платёжных матриц и решению матричных игр с помощью симпликс-метода. |
