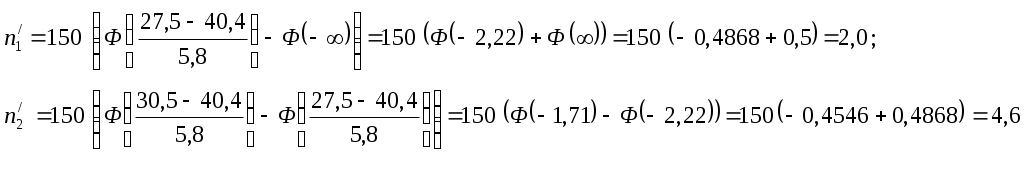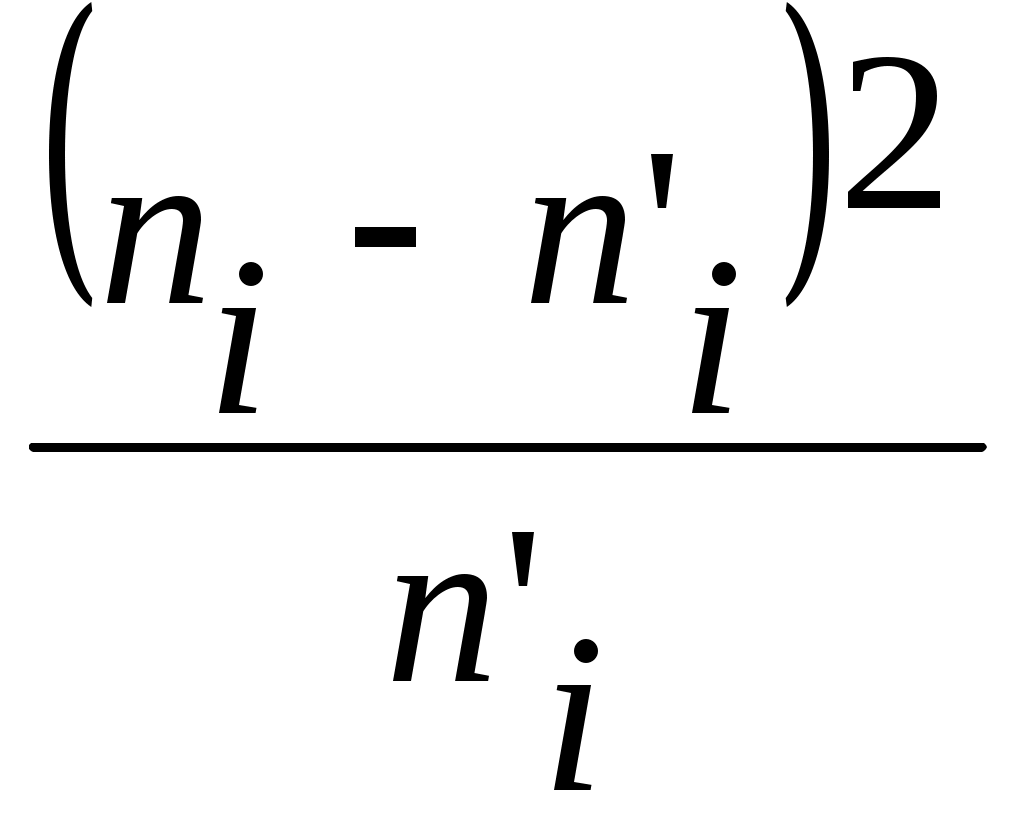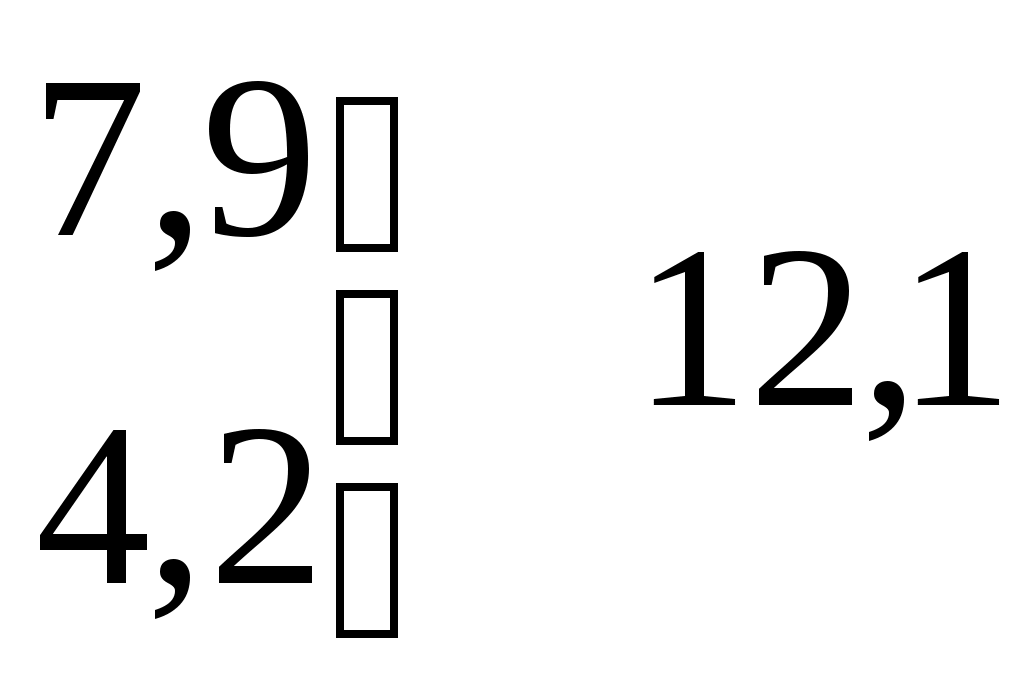|
|
теория вероятности. Теория. Решение задач типового варианта расчетной работы Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять
РАЗДЕЛ 2
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
РАСЧЕТНАЯ РАБОТА 2
ПОДБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ ПО ОПЫТНЫМ ДАННЫМ И ПРОВЕРКА ЕГО СОГЛАСИЯ ПО КРИТЕРИЮ 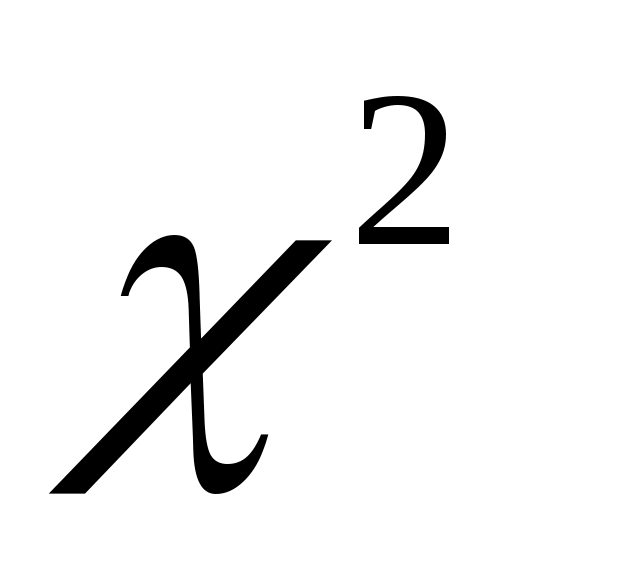
2.1 Задание для расчётной работы.
I. Из приложений 1 или 2 взять выборку объёма n. Выборку произвести методом, указанным преподавателем.
2. Построить гистограмму.
3. По виду гистограммы подобрать закон распределения случайной величины: нормальный, показательный, равномерный.
x
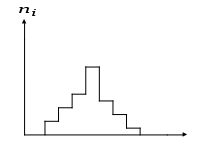
Рис. 1 (нормальный закон)
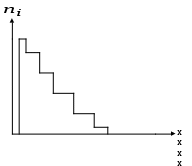
Рис. 2(показательный закон)
;
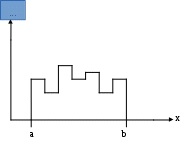
Рис.3( равномерный закон)
4. Проверить согласие закона распределения с опытными данными по критерию 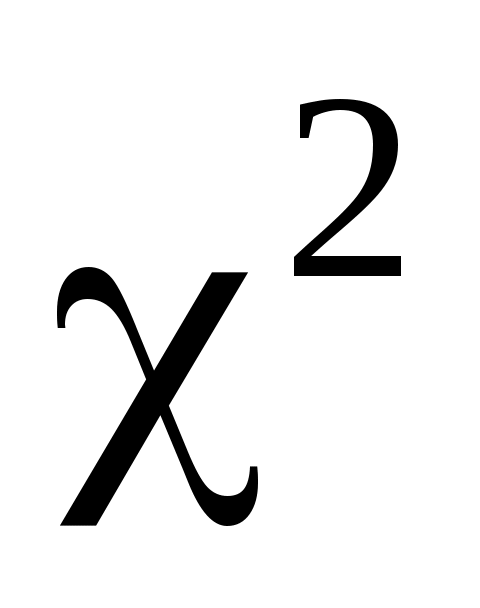 при уровне значимости при уровне значимости 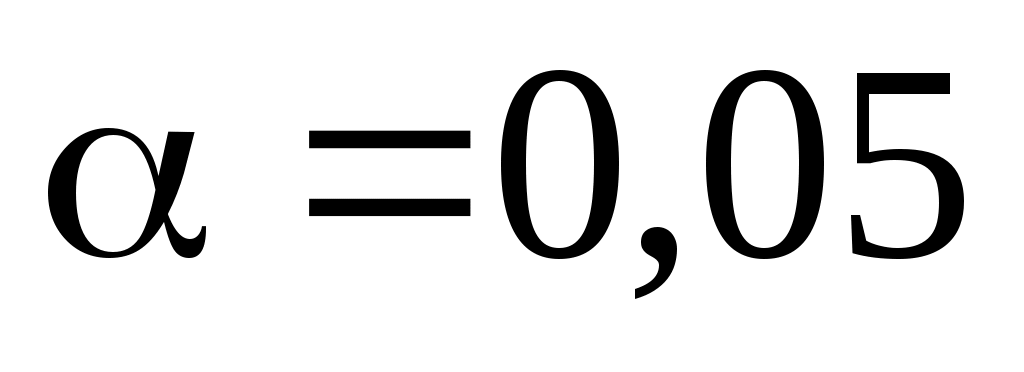 . .
5. Теоретическую кривую нанести на гистограмму опытных данных.
2.2 Проверка статистических гипотез
Важнейшим отделом математической статистики является проверка статистических гипотез.
Статистической называют гипотезу о виде неизвестного закона распределения, или о параметрах известных распределений случайной величины. Например, статистическими будут гипотезы: а) долговечность рассматриваемых деталей подчиняется нормальному закону распределения; б) дисперсии температур, полученные при одинаковых условиях в двух различных термостатах, равны между собой.
Выдвинутая гипотеза называется нулевой (основной). Выдвинутая гипотеза может быть правильной или неправильной и поэтому возникает необходимость её статистической проверки. Для проверки статистической гипотезы используют специально подобранную случайную величину 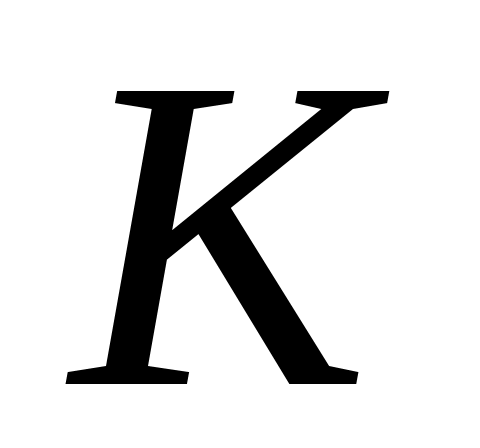 (критерий согласия), распределённую по некоторому закону. Из опытных данных находят наблюдаемое значение (критерий согласия), распределённую по некоторому закону. Из опытных данных находят наблюдаемое значение 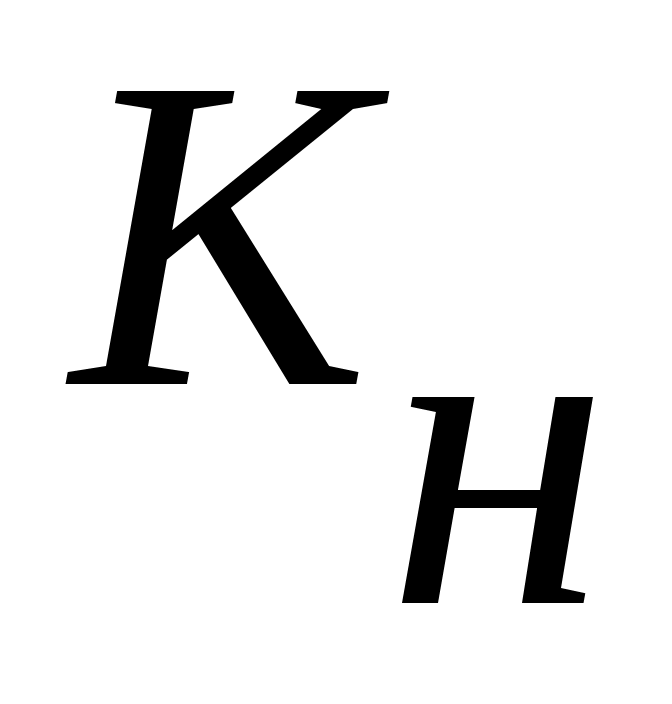 . Из специальных таблиц находят критическое значение . Из специальных таблиц находят критическое значение 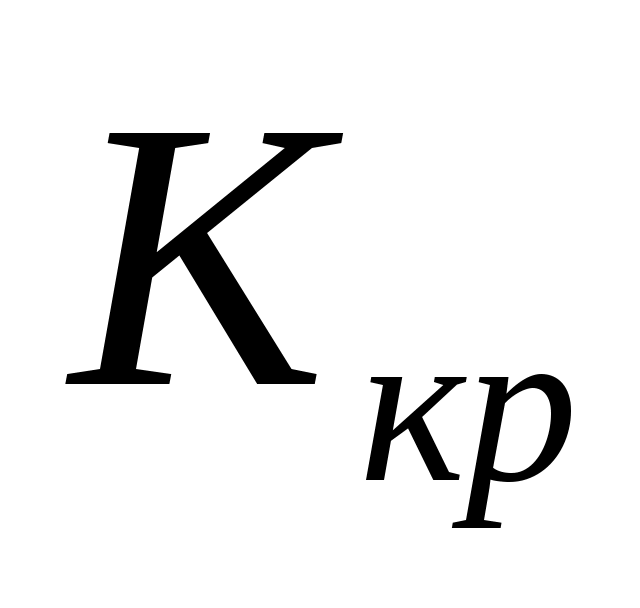 . Если . Если 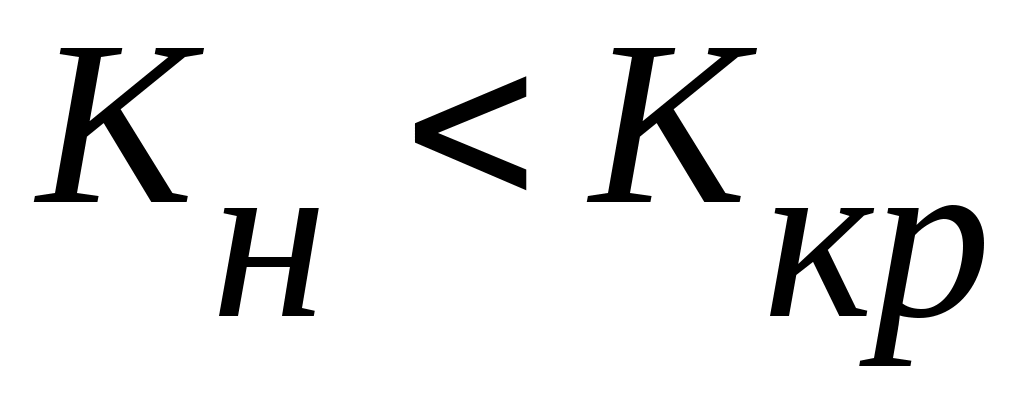 , то выдвинутая гипотеза (например, гипотеза о нормальном законе распределения) принимается, если , то выдвинутая гипотеза (например, гипотеза о нормальном законе распределения) принимается, если 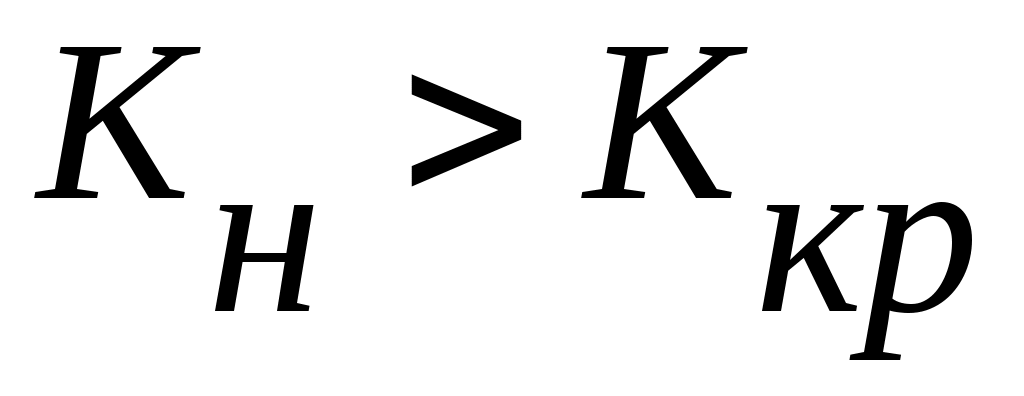 , выдвинутая гипотеза отвергается. , выдвинутая гипотеза отвергается.
Следует заметить, что условие 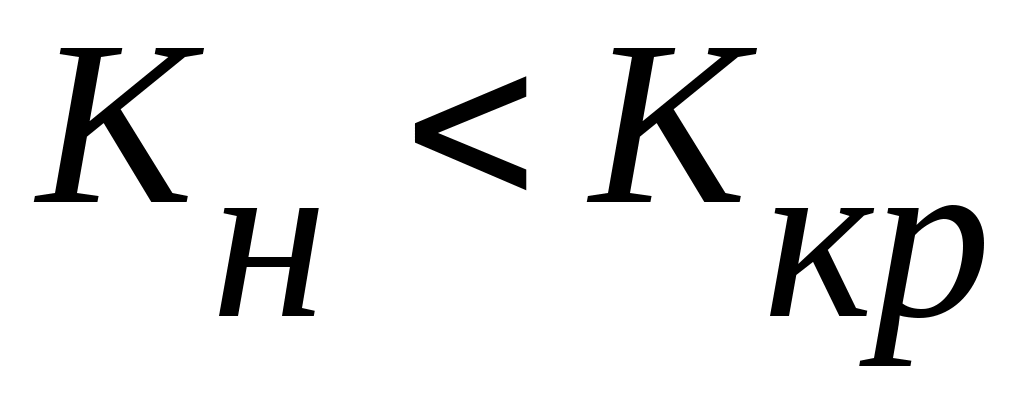 совсем не означает, что выдвинутая гипотеза доказана и является единственно верной; это означает лишь то, что гипотеза не противоречит опытным данным. совсем не означает, что выдвинутая гипотеза доказана и является единственно верной; это означает лишь то, что гипотеза не противоречит опытным данным.
Критерии проверки гипотезы о предполагаемом законе распределения называются критериями согласия. Имеется несколько критериев согласия: Пирсона, Колмогорова, Смирнова и др. Наиболее часто используется критерий Пирсона.
Критерий согласия Пирсона 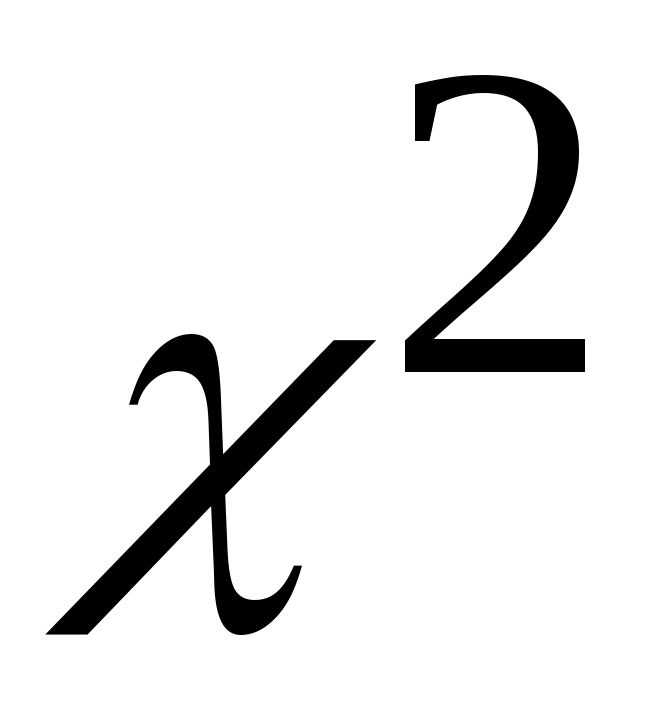 ( хи квадрат ) ( хи квадрат )
Критерий согласия 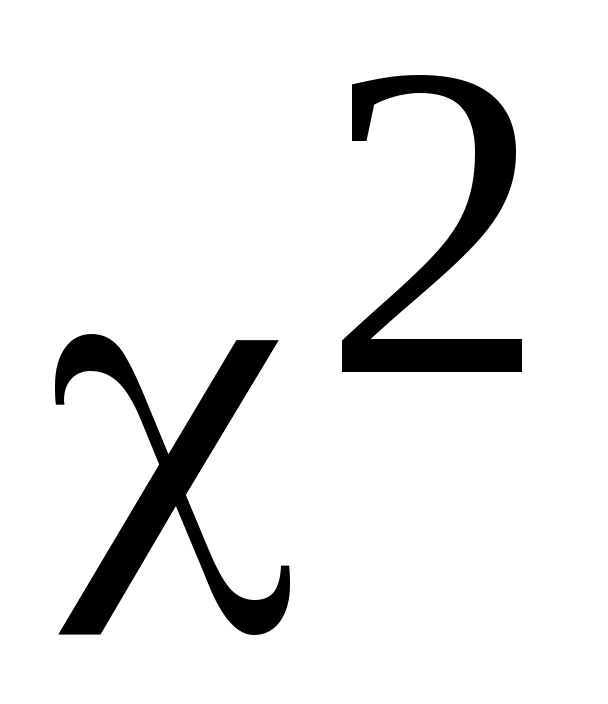 имеет наибольшее применение при проверке согласования теоретического и эмпирического законов распределения случайной величины. Наблюдаемое значение критерия вычисляется по формуле: имеет наибольшее применение при проверке согласования теоретического и эмпирического законов распределения случайной величины. Наблюдаемое значение критерия вычисляется по формуле: 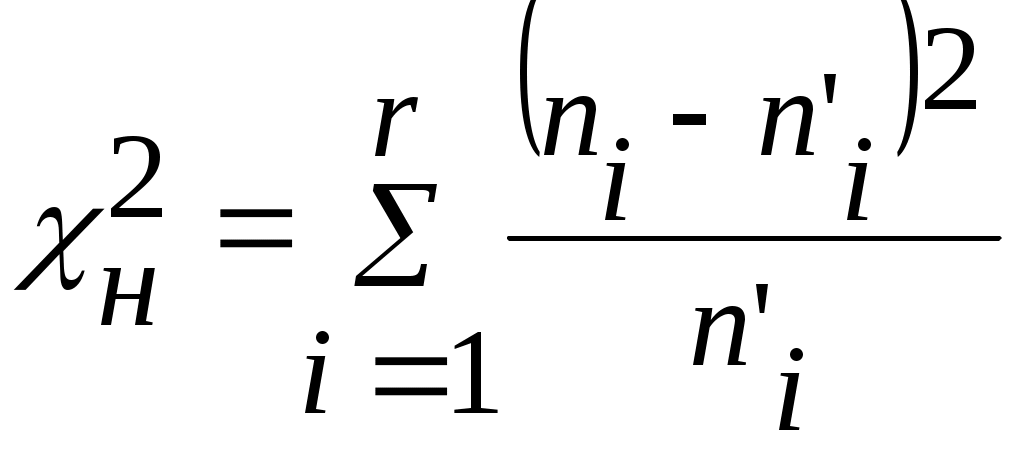 , (1) , (1)
где
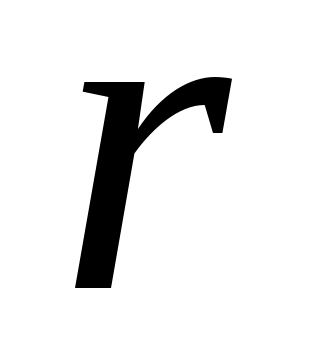 – число интервалов, на которые разбиты исходные опытные данные; – число интервалов, на которые разбиты исходные опытные данные;
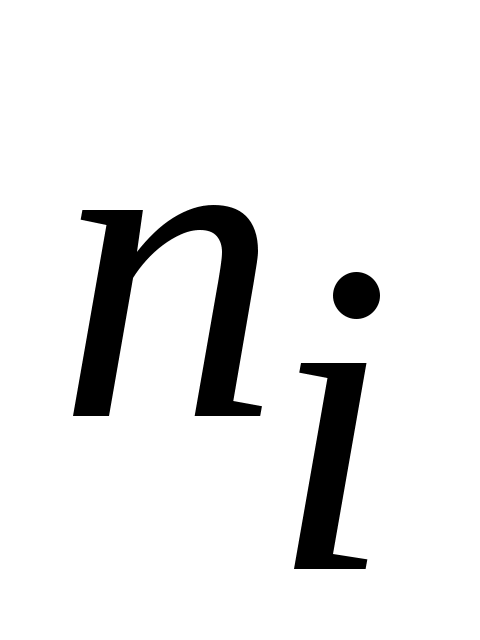 - число опытных данных, попавших в - число опытных данных, попавших в  интервал; интервал;
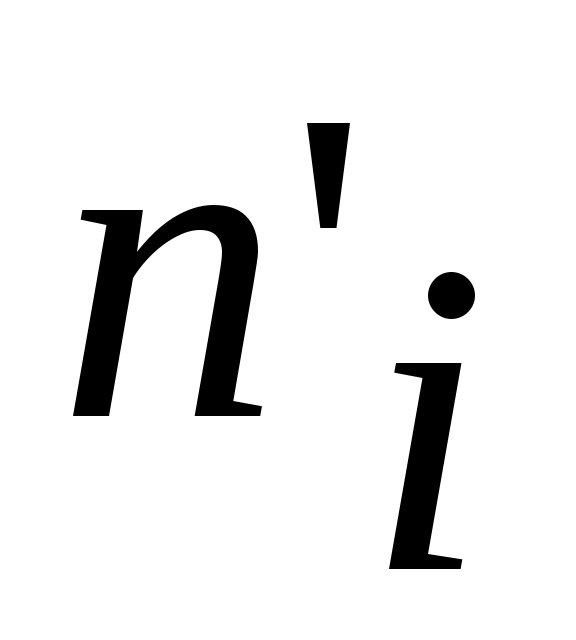 - теоретическое число, попавшее в - теоретическое число, попавшее в 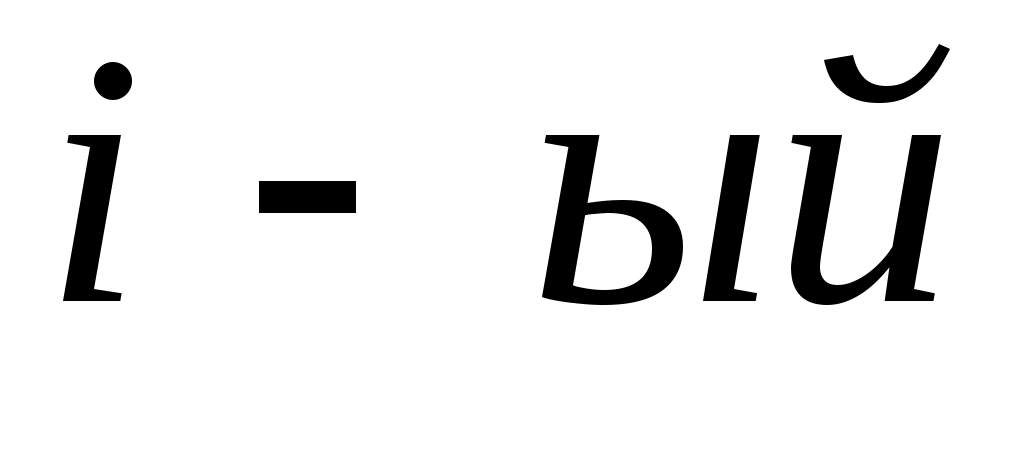 интервал, находится по формуле: интервал, находится по формуле:
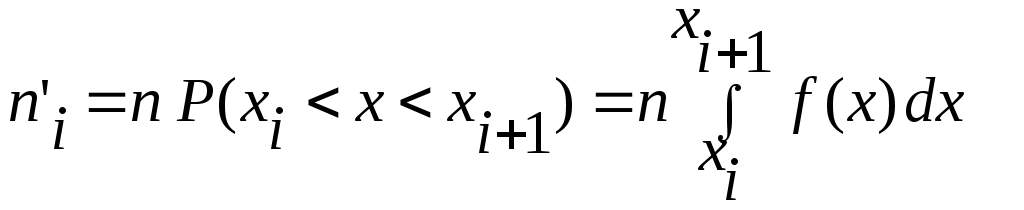 , (2) , (2)
( 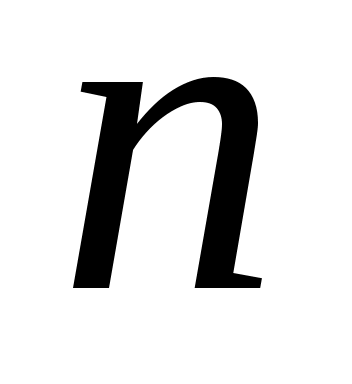 – объём выборки). – объём выборки).
В случае нормального закона
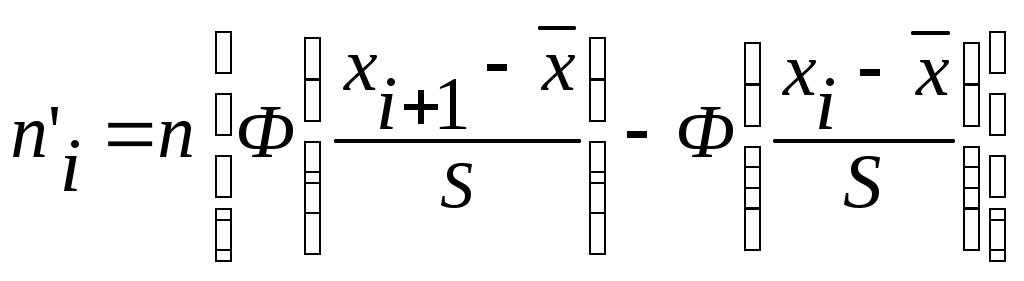 , (3) , (3)
где 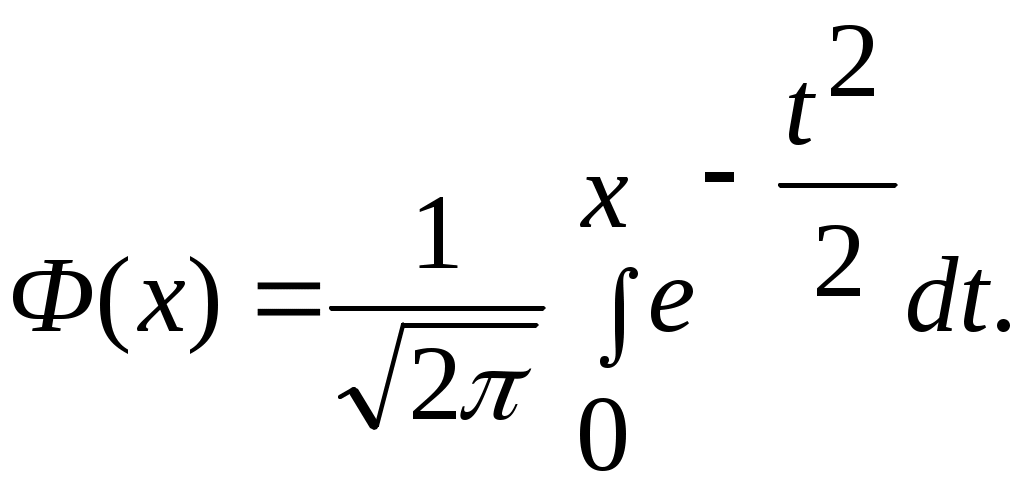 (4) (4)
В случае показательного закона
 . (5) . (5)
В случае для равномерного закона распределения
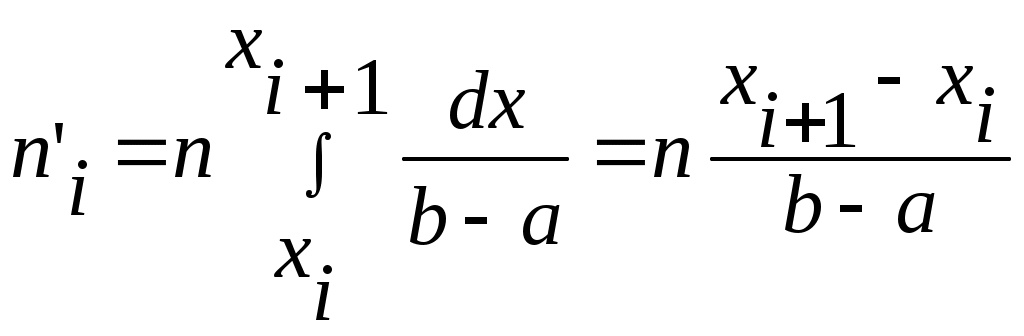 . (6) . (6)
При практическом использовании критерия согласия 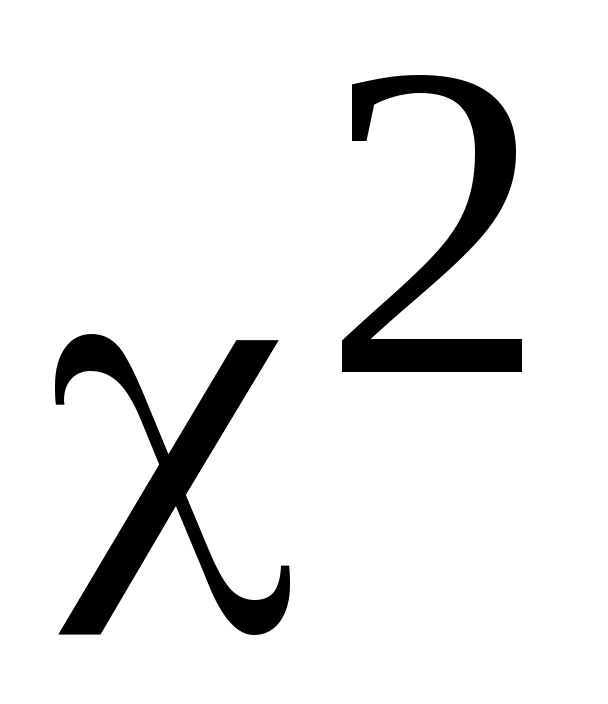 необходимо учесть следующие замечания: необходимо учесть следующие замечания:
1. Число опытных данных при использовании критерия 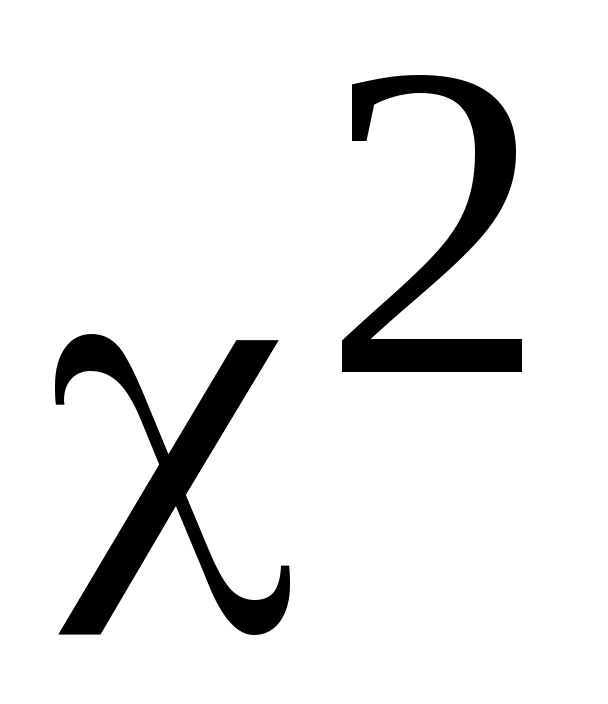 должно быть достаточно большим: должно быть достаточно большим: 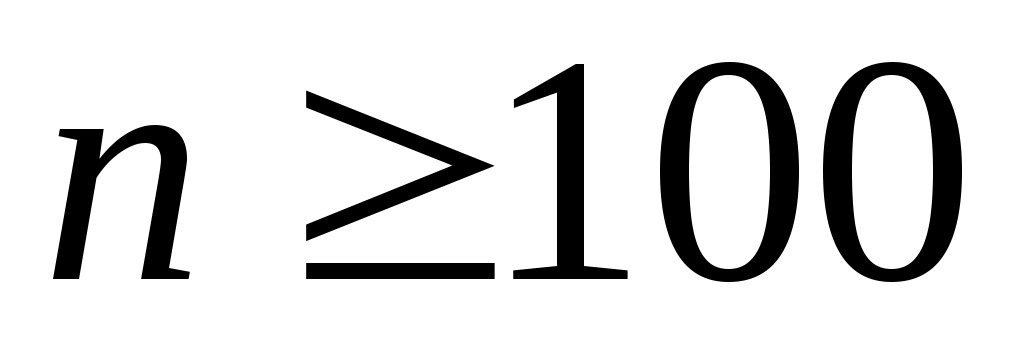 (критерий справедлив при (критерий справедлив при  ). ).
2. Рекомендуется иметь в каждом интервале не менее 5-10 наблюдений 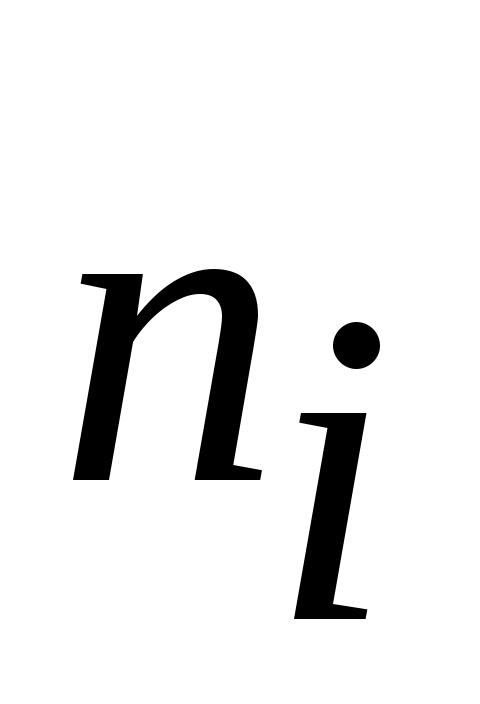 . Если . Если 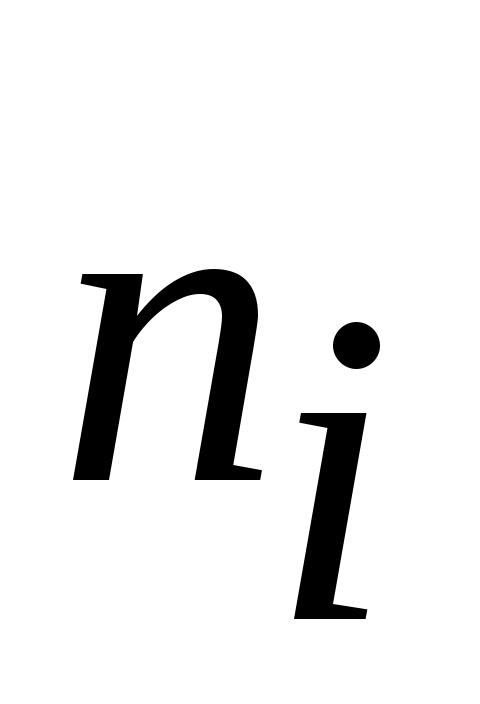 в отдельных интервалах очень малы, следует объединить интервалы в один, суммируя частоты. В соответствии с этим число исходных интервалов должно быть уменьшено. в отдельных интервалах очень малы, следует объединить интервалы в один, суммируя частоты. В соответствии с этим число исходных интервалов должно быть уменьшено.
3. Уровень значимости 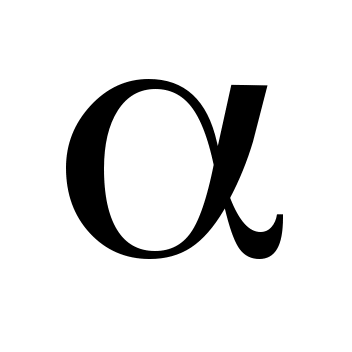 - вероятность ошибки 1-го рода, т.е. вероятность ошибки отвергнуть выдвинутую гипотезу, когда в действительности она верна. Чаще всего берут - вероятность ошибки 1-го рода, т.е. вероятность ошибки отвергнуть выдвинутую гипотезу, когда в действительности она верна. Чаще всего берут 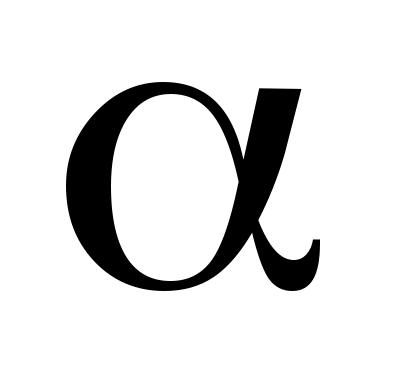 =0,05, но встречаются и другие уровни значимости. =0,05, но встречаются и другие уровни значимости.
4. 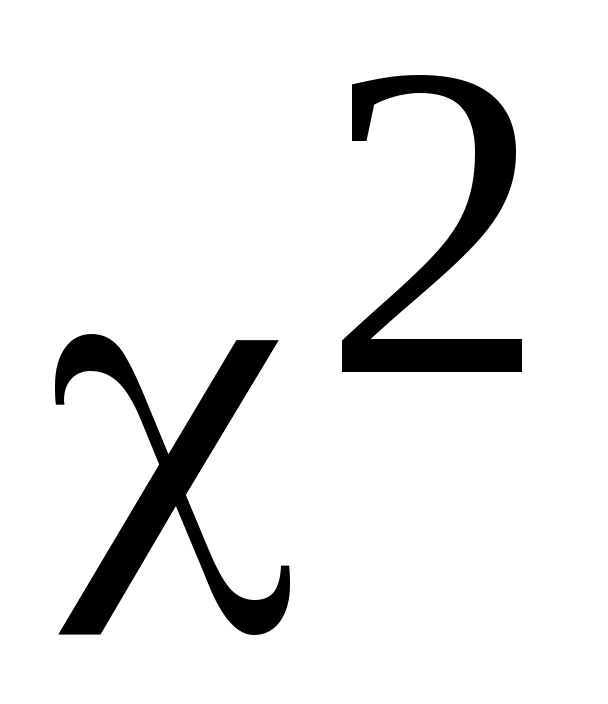 - распределение зависит от числа степеней свободы, это число находится по формуле - распределение зависит от числа степеней свободы, это число находится по формуле
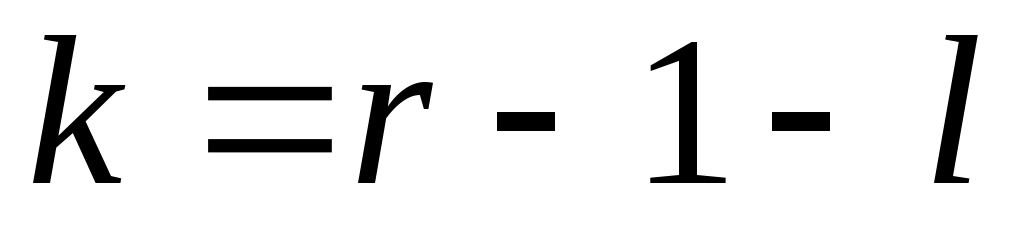 , (7) , (7)
где
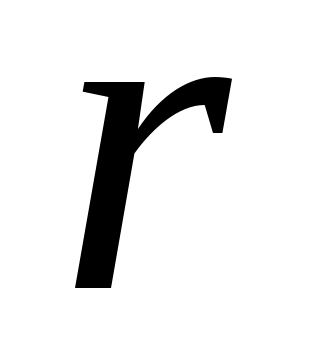 – число интервалов, на которые разбиты статистические данные; – число интервалов, на которые разбиты статистические данные;
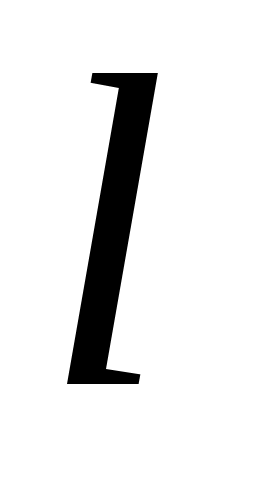 - число параметров предполагаемого теоретического закона, использованных для вычисления теоретических частот и оцениваемых по выборке. - число параметров предполагаемого теоретического закона, использованных для вычисления теоретических частот и оцениваемых по выборке.
Если предполагаемое распределение нормальное, то по выборке оценивают два параметра 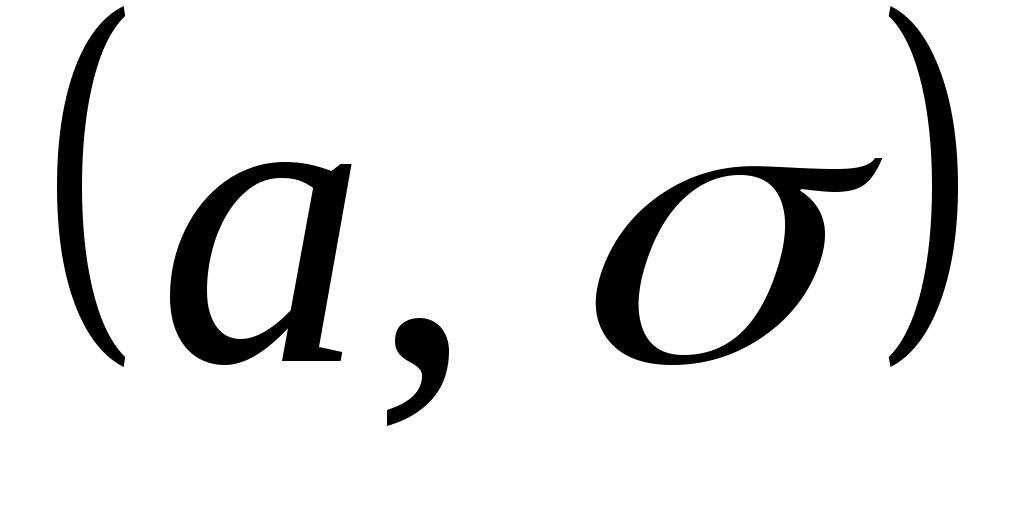 , поэтому число степеней свободы , поэтому число степеней свободы 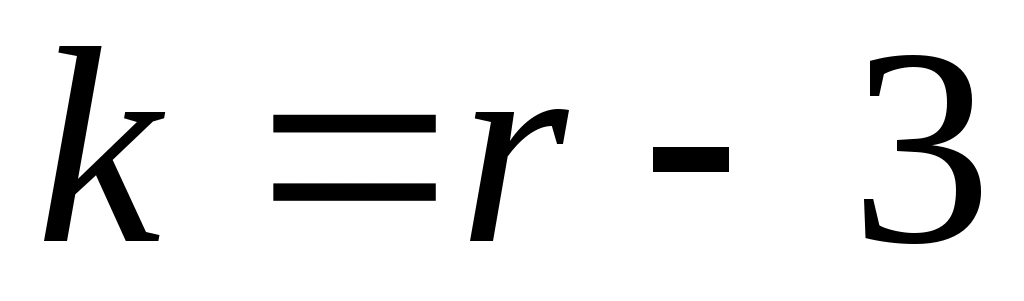 . Таким же будет число степеней свободы в случае равномерного закона распределения (оцениваемые параметры а и b). В случае показательного закона распределения по выборке оценивают один параметр, следовательно, в этом случае . Таким же будет число степеней свободы в случае равномерного закона распределения (оцениваемые параметры а и b). В случае показательного закона распределения по выборке оценивают один параметр, следовательно, в этом случае 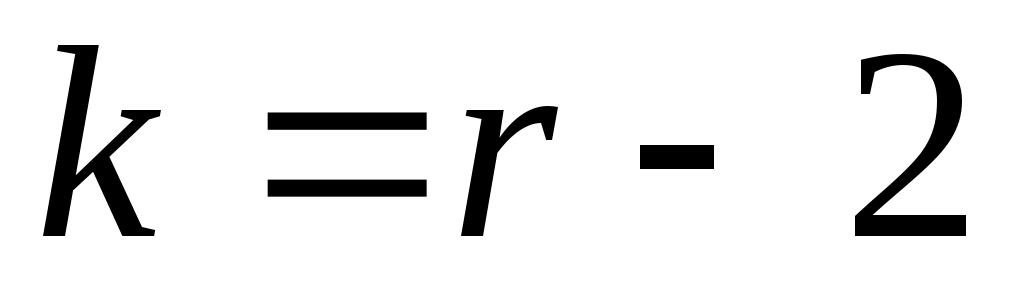 . .
5. По заданному уровню значимости 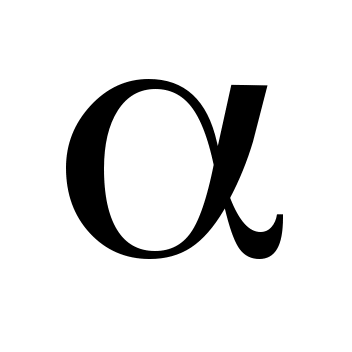 и числу степеней свободы и числу степеней свободы 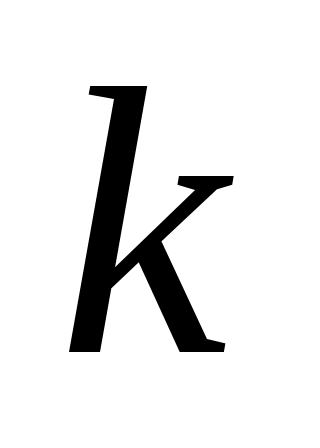 из таблицы распределения из таблицы распределения 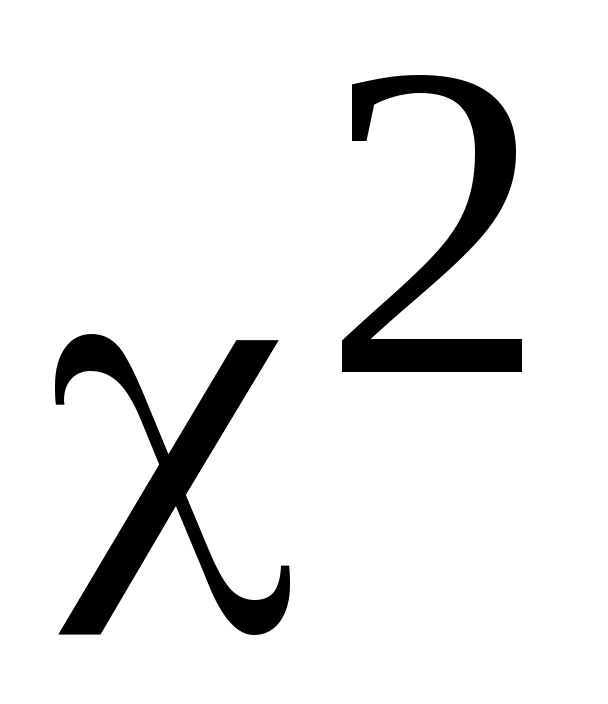 (приложение 5) находят значение (приложение 5) находят значение 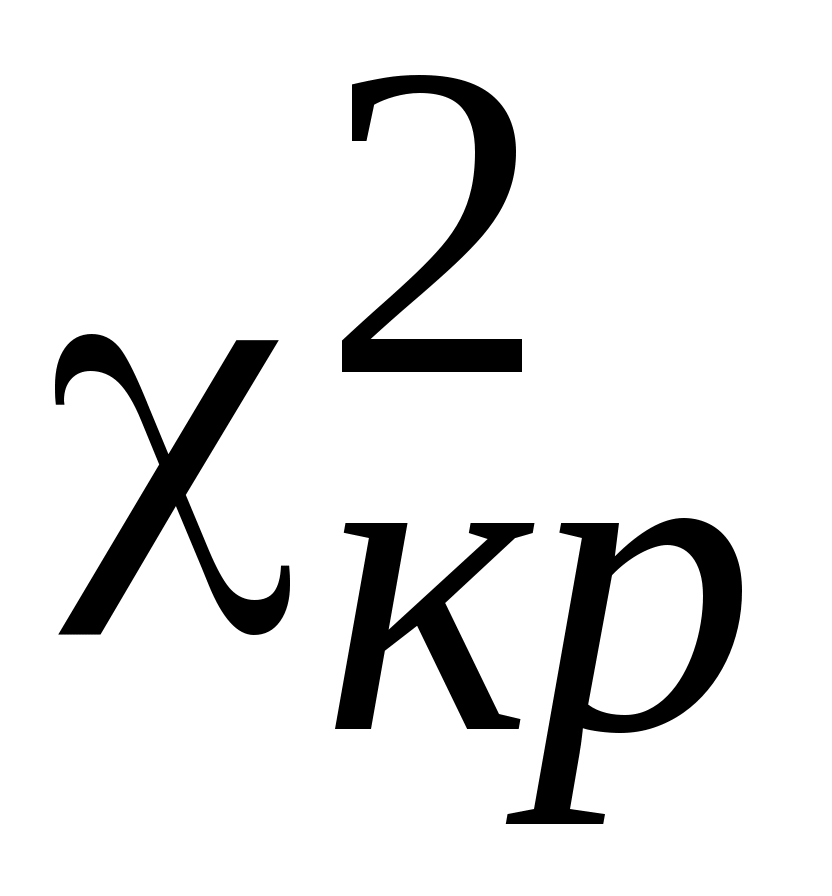 . .
6. Если 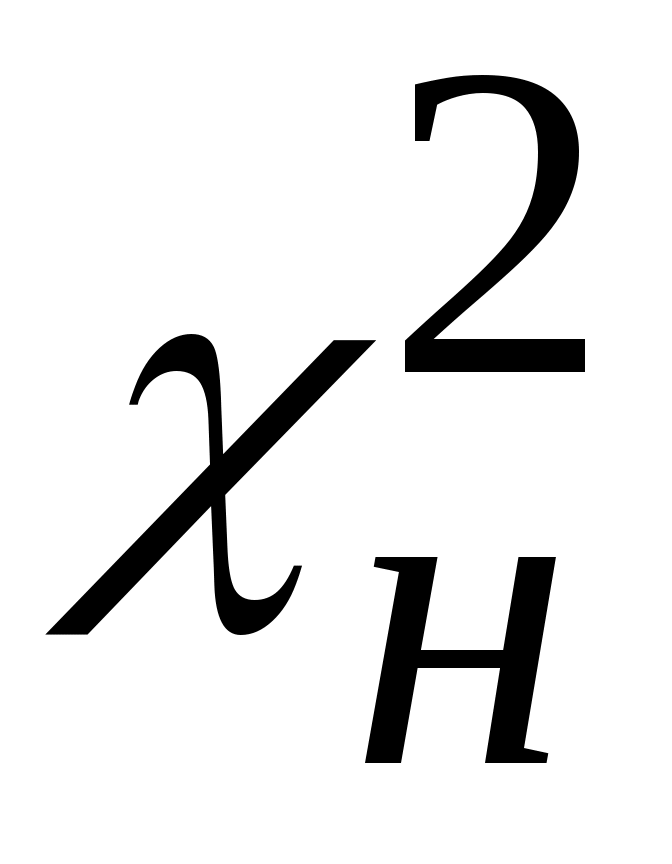 < <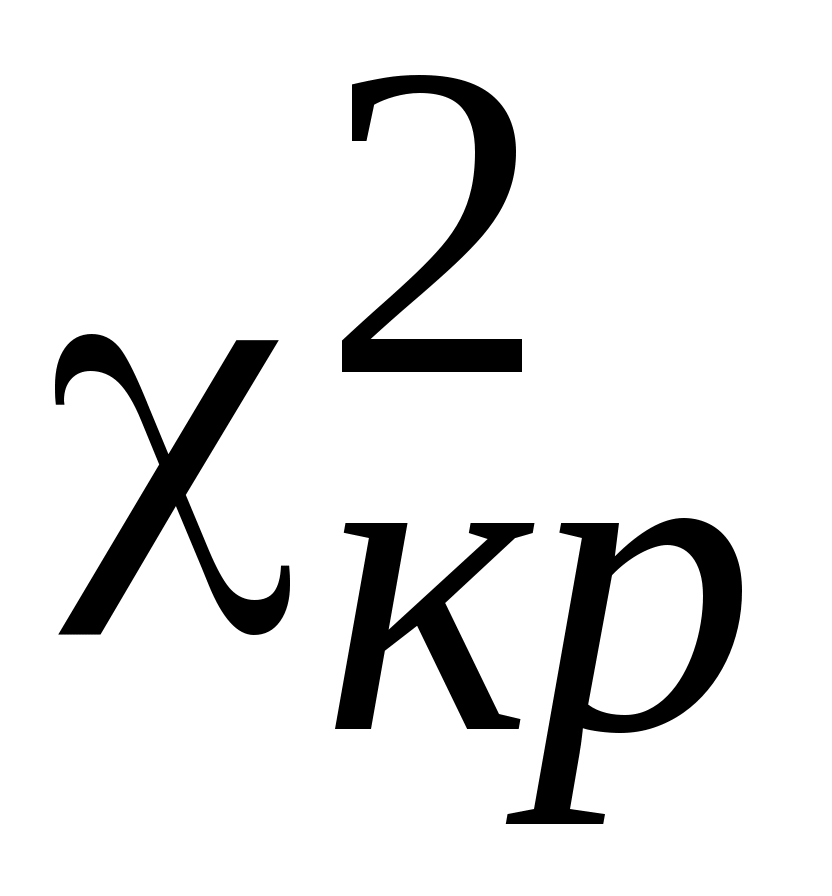 , то гипотеза о виде закона не отвергается. , то гипотеза о виде закона не отвергается.
2.3 Методические указания к выполнению расчетной работы
2.3.1 Проверка гипотезы о нормальном распределении генеральной совокупности
1. По данной выборке построить эмпирическое распределение в виде последовательности равноотстоящих вариант и соответствующих им частот, для чего:
а) упорядочить выборку по возрастанию, найти 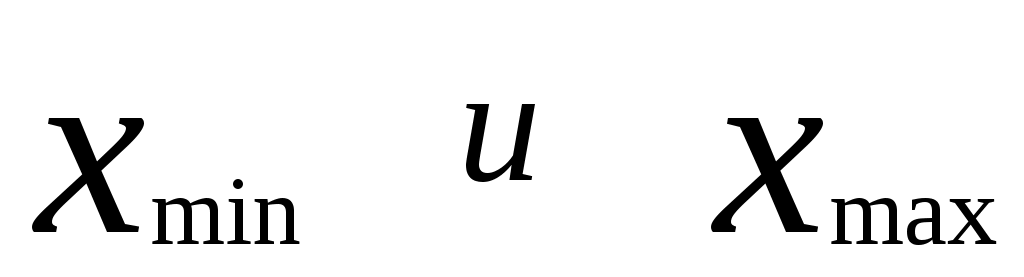 ; ;
б) весь интервал, в который попали опытные данные, разбить на r частичных интервалов 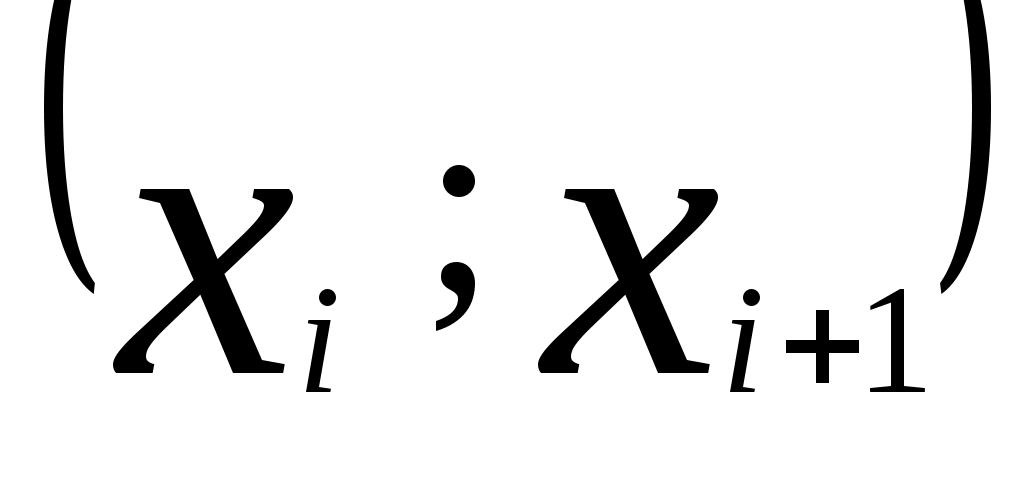 одинаковой длины. Для определения длин частичных интервалов рекомендуется формула одинаковой длины. Для определения длин частичных интервалов рекомендуется формула
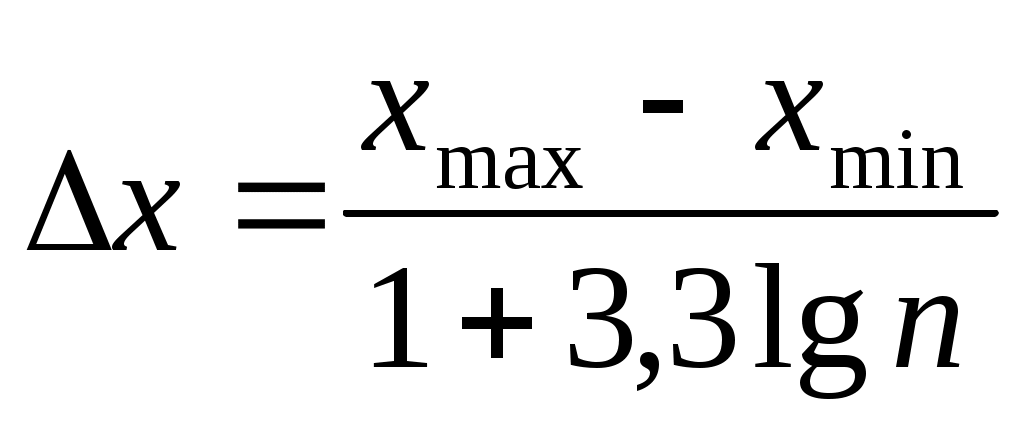 . (8) . (8)
За длину частичного интервала принимается некоторое удобное число, ближайшее к полученному значению 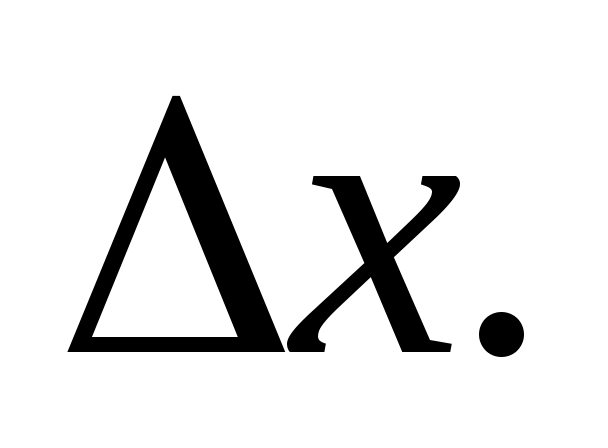 Границы интервалов выбираются так, чтобы результаты измерений не совпали с границами интервалов. Начало первого интервала сдвинуть влево от значения Границы интервалов выбираются так, чтобы результаты измерений не совпали с границами интервалов. Начало первого интервала сдвинуть влево от значения 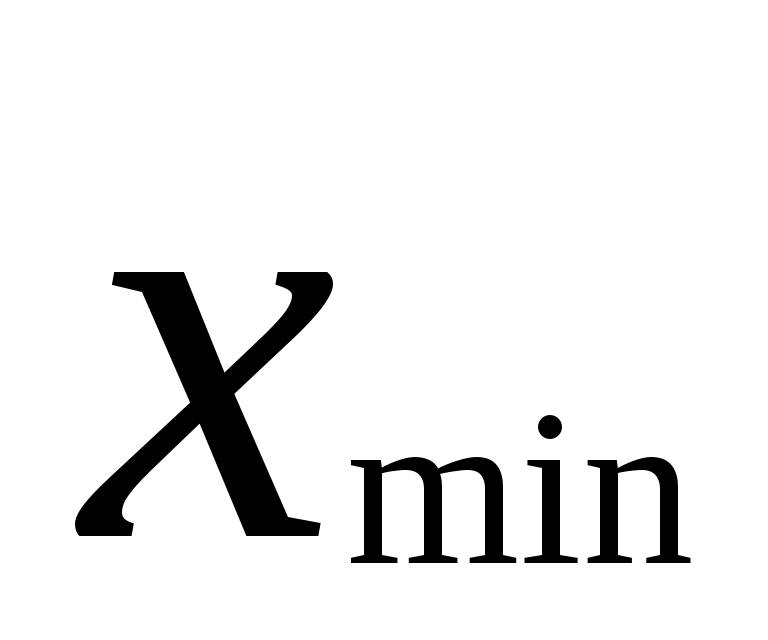 (например, взять (например, взять 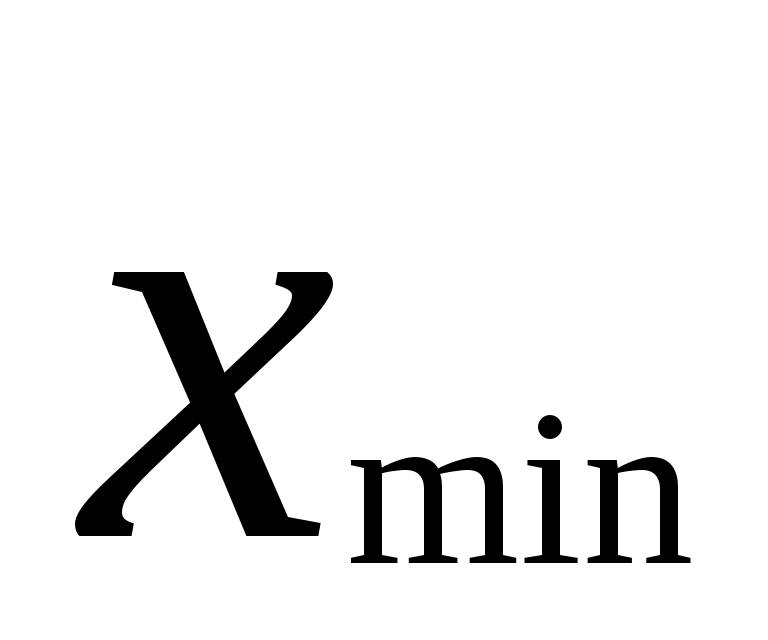 - 0,5); - 0,5);
в) для каждого частичного интервала 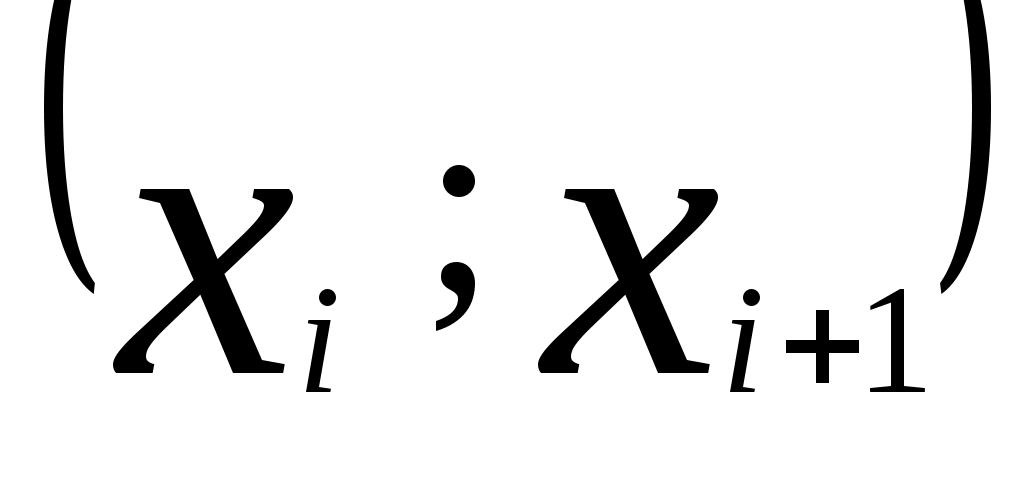 найти найти 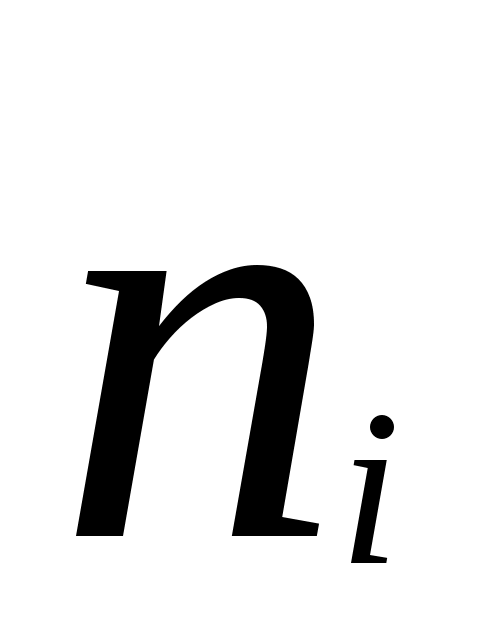 - сумму частот вариант и считать, что - сумму частот вариант и считать, что 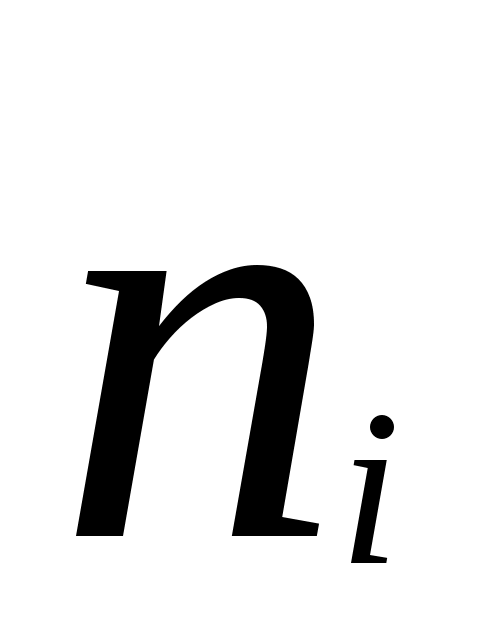 сосредоточено в серединеi-го интервала, т.е. взять сосредоточено в серединеi-го интервала, т.е. взять 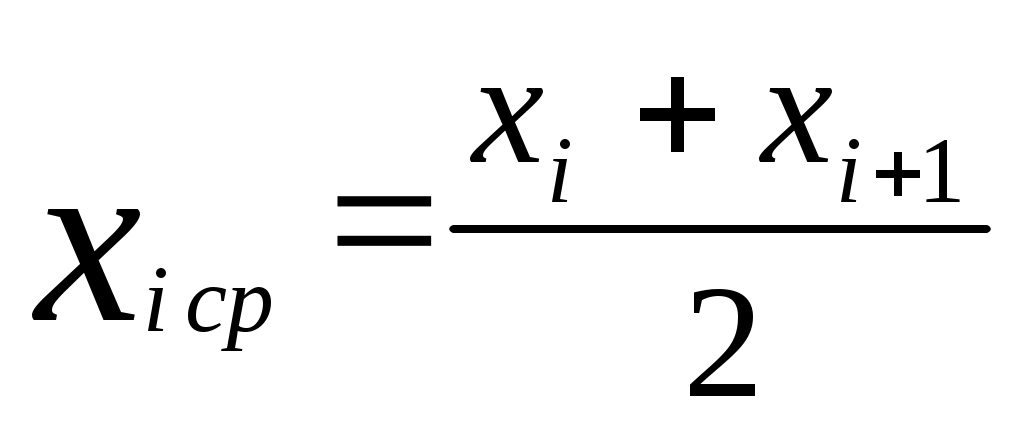 . .
2. Построить гистограмму частот.
3. Найти выборочную среднюю 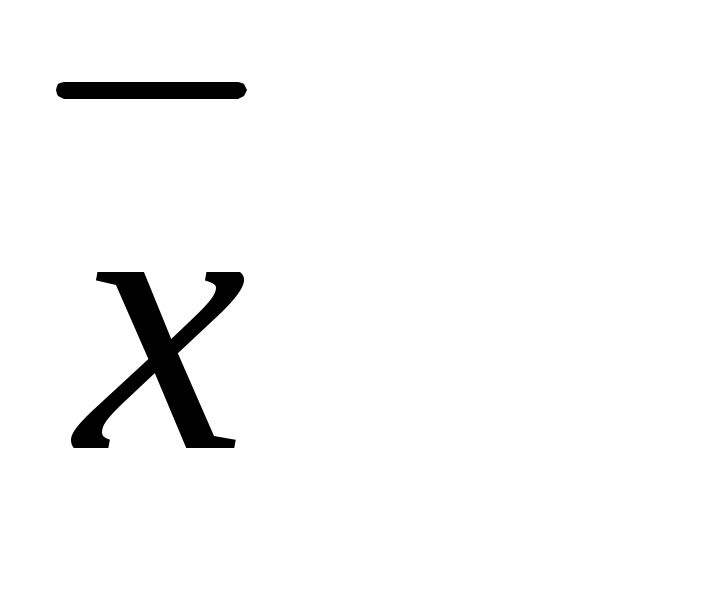 и выборочное среднее квадратическое отклонение S по формулам: и выборочное среднее квадратическое отклонение S по формулам:
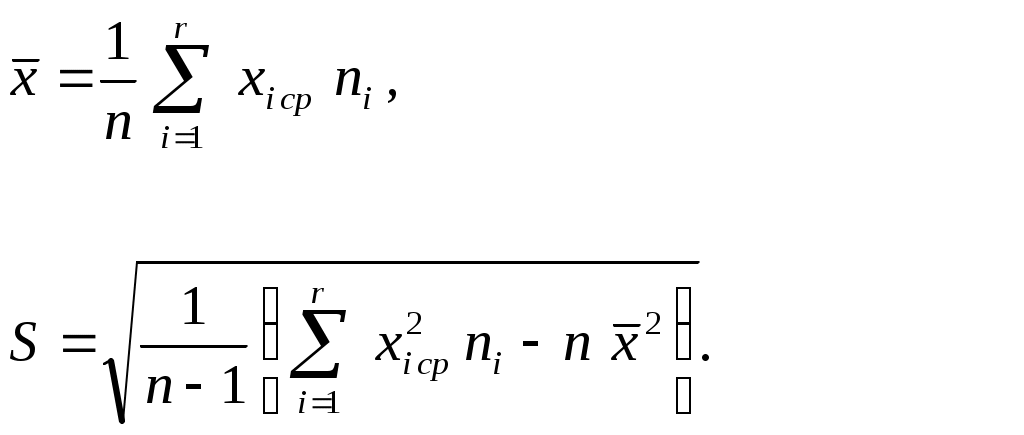 (9) (9)
4. Найти теоретические частоты 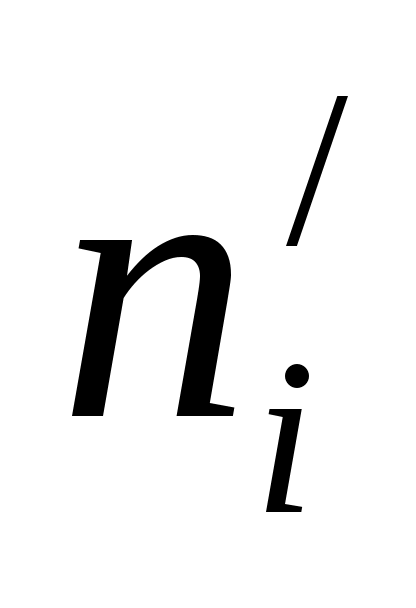 , попавшие в i - ый интервал, по формуле (3);. , попавшие в i - ый интервал, по формуле (3);.
5. Вычислить наблюдаемое значение критерия 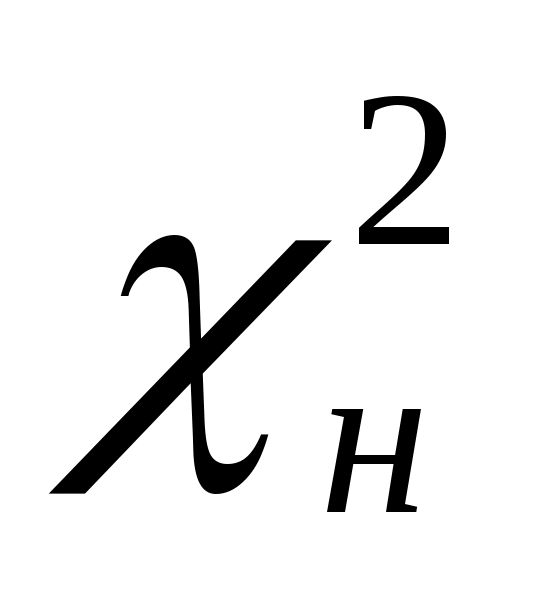 по формуле (1); по формуле (1);
6. По таблице 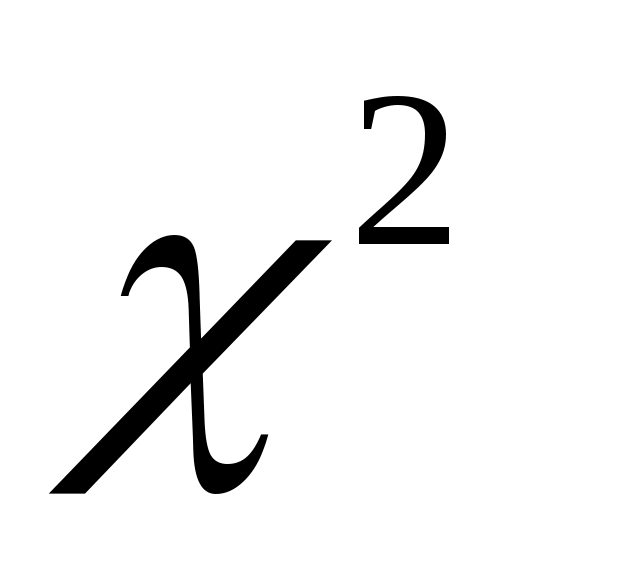 - распределения при уровне значимости - распределения при уровне значимости 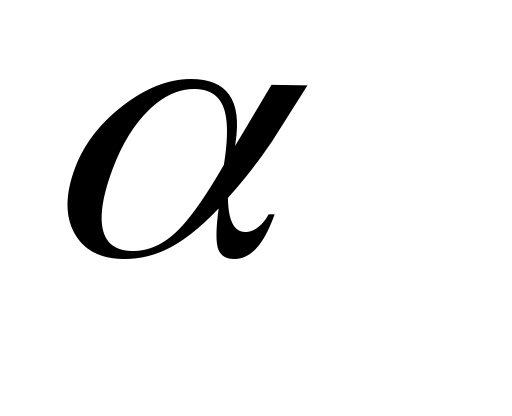 =0,05 и числе степеней свободы kнайти критическое значение =0,05 и числе степеней свободы kнайти критическое значение 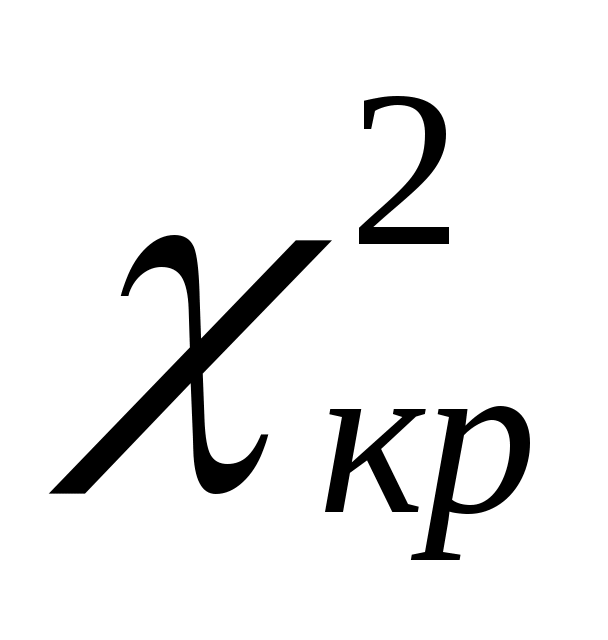 (приложение 5). (приложение 5).
7. Сравнить два значения 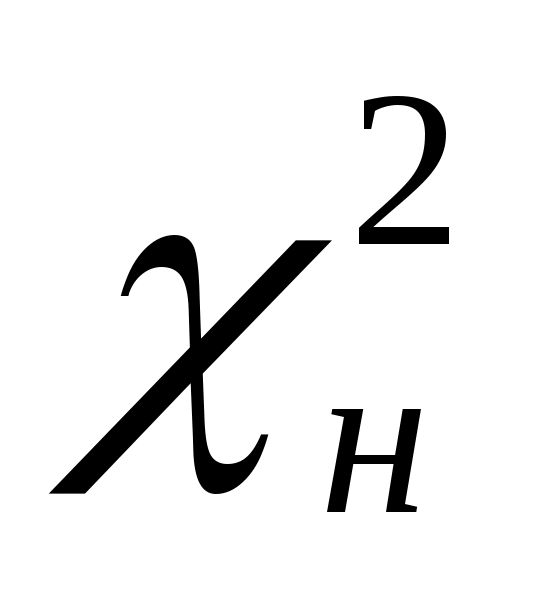 и и 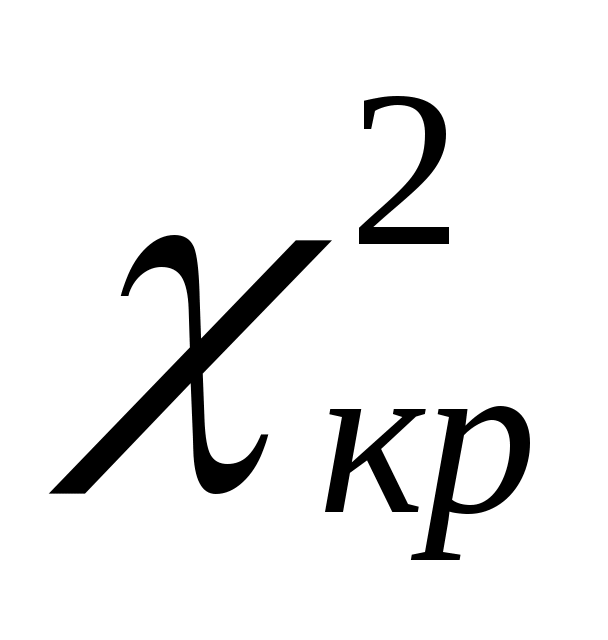 . Если . Если 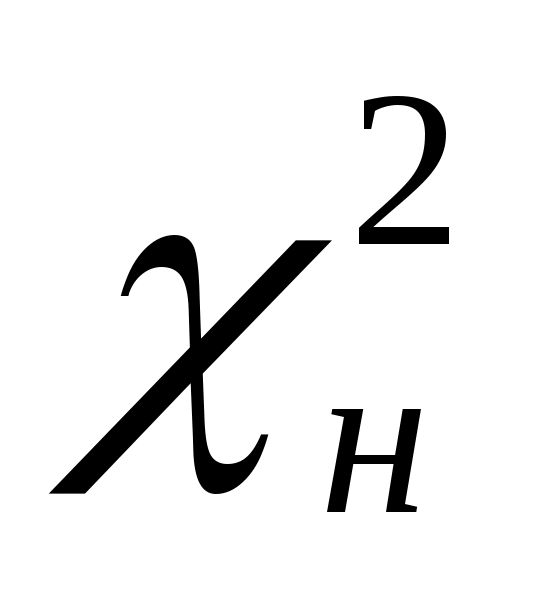 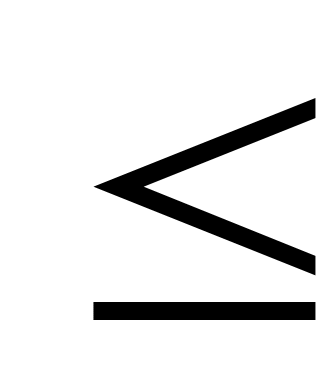 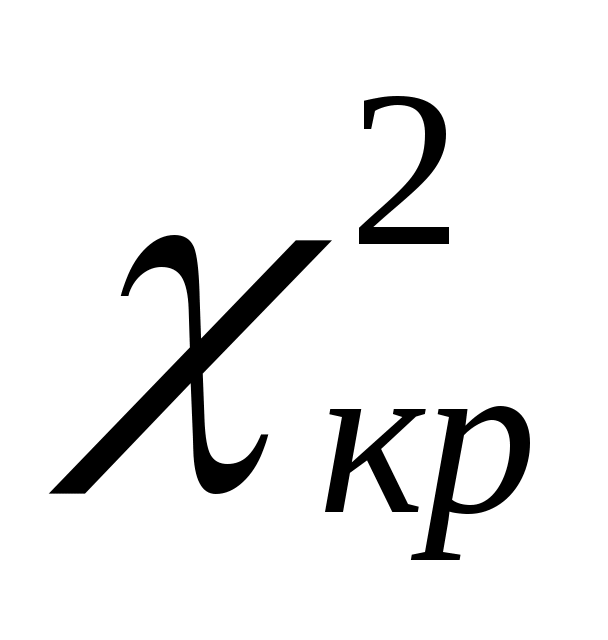 , то нулевая гипотеза не отвергается, т.е. в этом случае отклонения от предполагаемого теоретического закона считаются незначительными. Если , то нулевая гипотеза не отвергается, т.е. в этом случае отклонения от предполагаемого теоретического закона считаются незначительными. Если 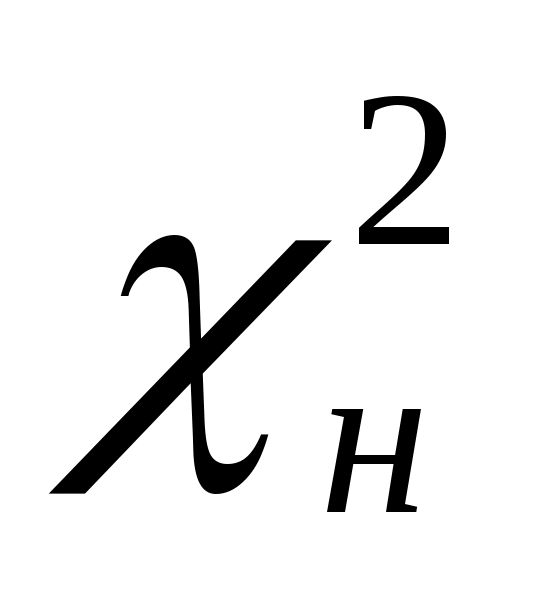 > >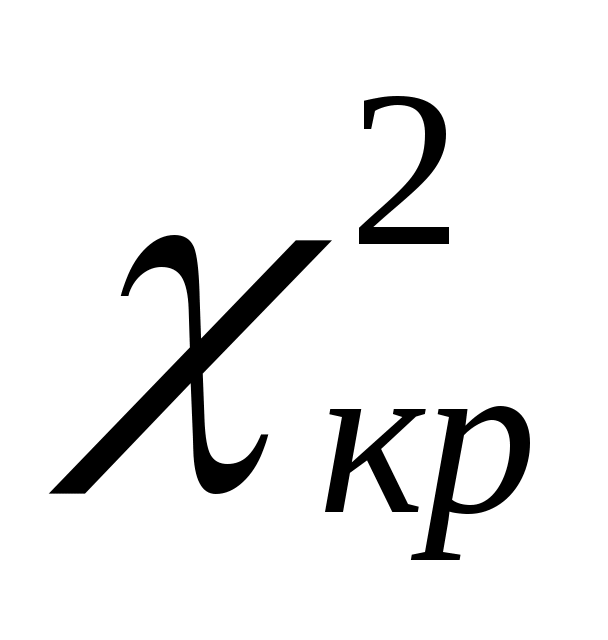 , то нулевая гипотеза отвергается. , то нулевая гипотеза отвергается.
Пример 1 Контролировался диаметр у 150 цапф передней оси, изготовленных на токарном станке. В результате были получены следующие значения положительных отклонений в микронах (мк) от номинального размера 20 мк
48
|
39
|
43
|
36
|
39
|
34
|
32
|
48
|
46
|
37
|
25
|
31
|
34
|
36
|
35
|
37
|
45
|
49
|
49
|
44
|
43
|
46
|
34
|
48
|
43
|
36
|
41
|
34
|
42
|
35
|
38
|
40
|
46
|
34
|
39
|
41
|
38
|
39
|
36
|
42
|
30
|
43
|
41
|
39
|
37
|
33
|
35
|
42
|
45
|
43
|
37
|
42
|
38
|
40
|
34
|
39
|
32
|
40
|
39
|
37
|
43
|
30
|
44
|
45
|
37
|
34
|
49
|
41
|
51
|
32
|
37
|
30
|
50
|
32
|
32
|
35
|
45
|
42
|
41
|
48
|
43
|
45
|
44
|
46
|
42
|
39
|
41
|
38
|
31
|
32
|
40
|
52
|
45
|
47
|
35
|
45
|
33
|
38
|
36
|
40
|
44
|
52
|
44
|
34
|
44
|
44
|
43
|
43
|
40
|
30
|
32
|
42
|
49
|
39
|
42
|
43
|
48
|
41
|
43
|
42
|
40
|
48
|
35
|
42
|
44
|
44
|
34
|
33
|
48
|
51
|
44
|
50
|
47
|
34
|
33
|
33
|
40
|
46
|
50
|
43
|
44
|
50
|
40
|
40
|
35
|
35
|
41
|
42
|
42
|
47
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверить согласие нормального закона распределения с опытными данными по критерию Пирсона при уровне значимости 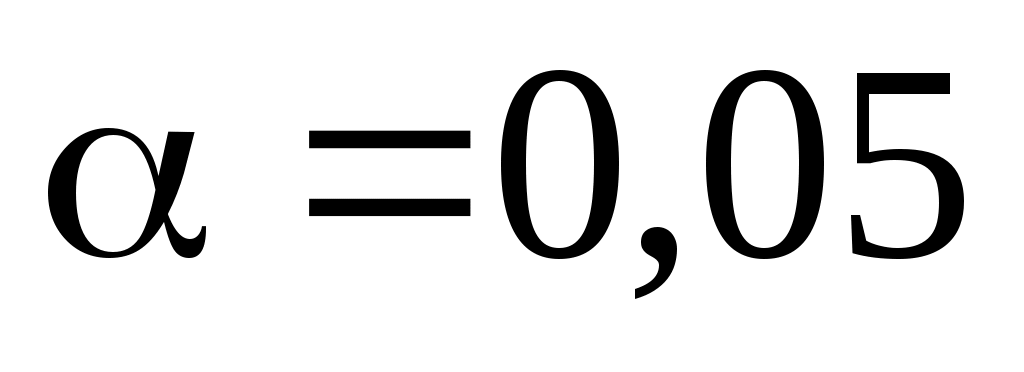 . .
Решение
1.Случайную величину (отклонения от номинального размера) обозначим 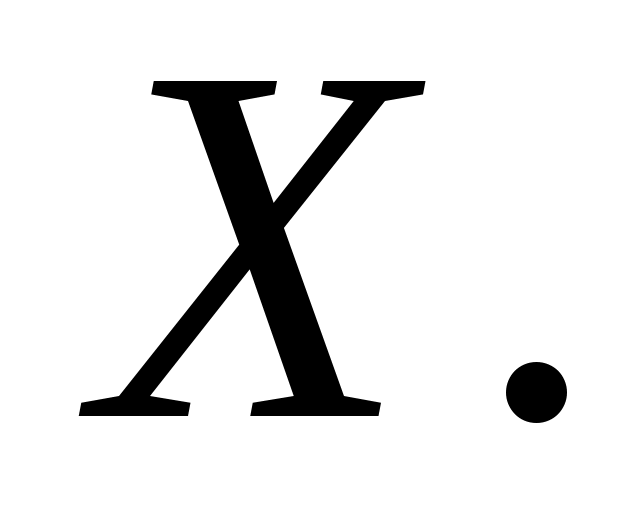
Из выборки приведённого примера находим: 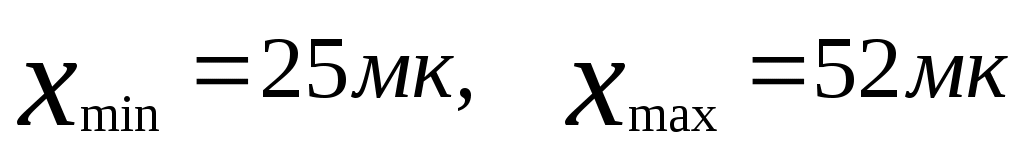 . .
Вычисляем: 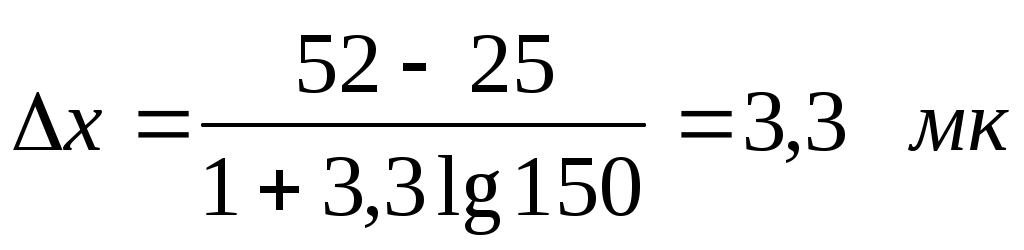 . .
Возьмём длину частичного интервала 3мк. Левый конец первого интервала возьмём 24,5мк. Из данной выборки найдём число опытных данных, попавших в каждый частичный интервал.
Полученные данные сведём в таблицу 1.
Таблица 1
i
|
|
|
№
|
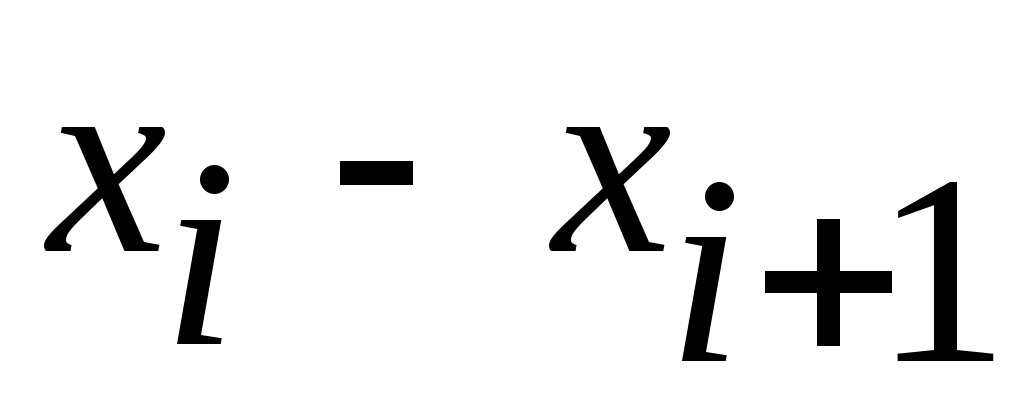
|
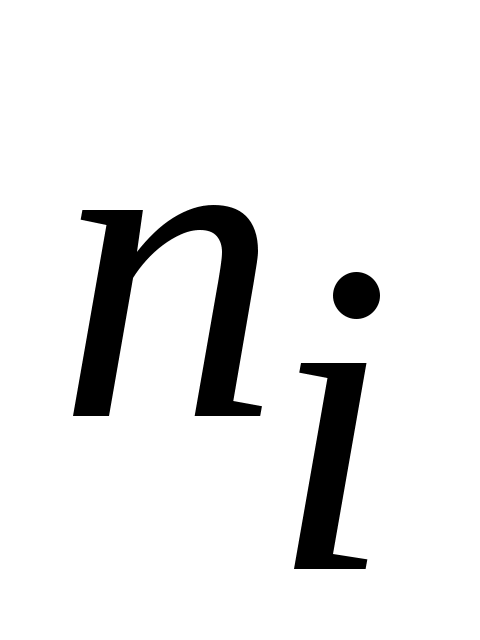
|
1
|
24,5 - 27,5
|
1
|
6
|
39,5 - 42,5
|
30
|
2
|
27,5 - 30,5
|
4
|
7
|
42,5 - 45,5
|
29
|
3
|
30,5 - 33,5
|
13
|
8
|
45,5 - 48,5
|
16
|
4
|
33,5 - 36,5
|
23
|
9
|
48,5 - 51,5
|
10
|
5
|
36,5 - 39,5
|
22
|
10
|
51,5 - 54,5
|
2
|
2. Для каждого частичного интервала найдем 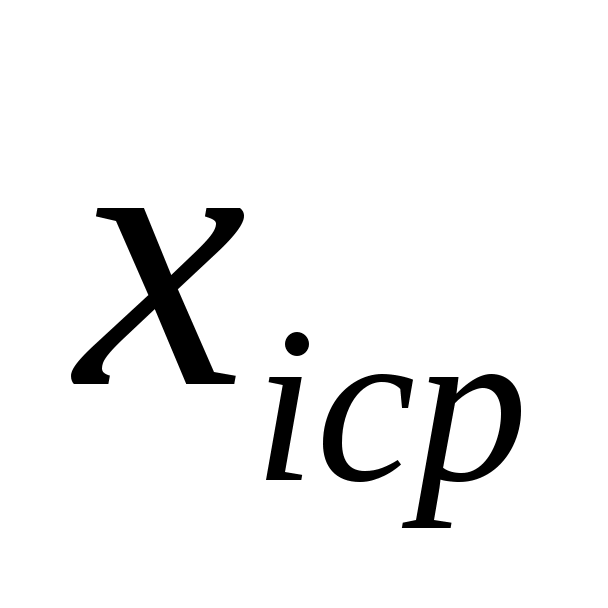 : : 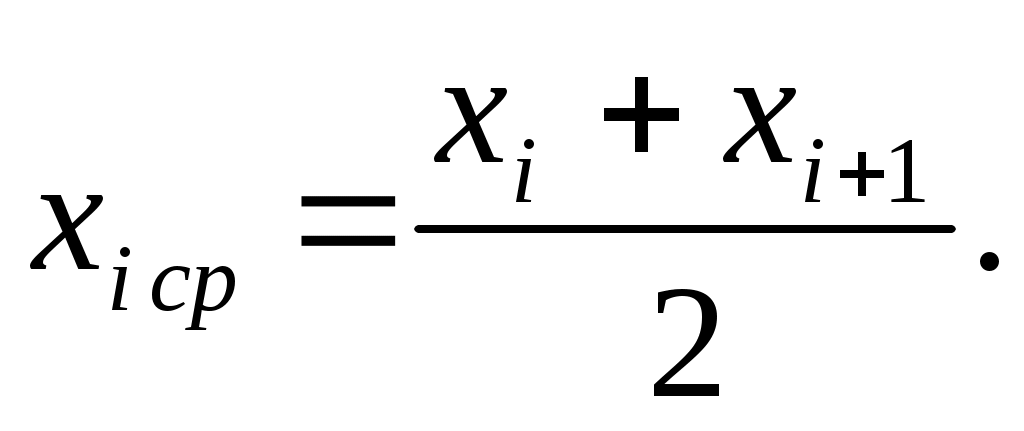 Вычислим значения Вычислим значения 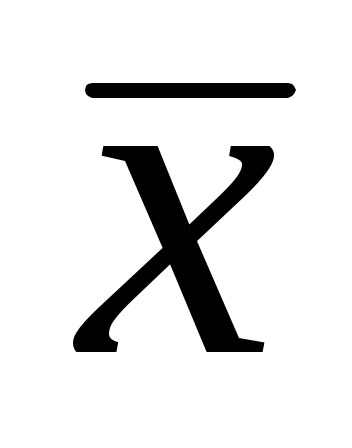 и S по формулам (9); расчеты поместим в таблицу 2. и S по формулам (9); расчеты поместим в таблицу 2.
Таблица 2
-
i
|
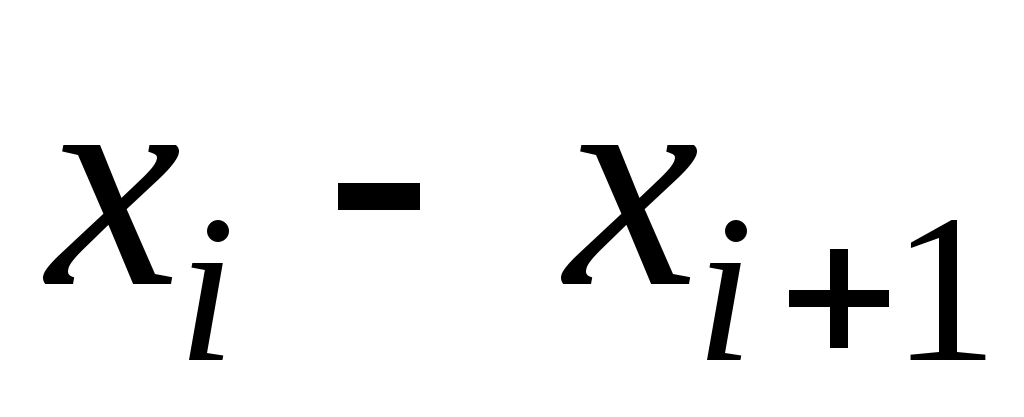
|
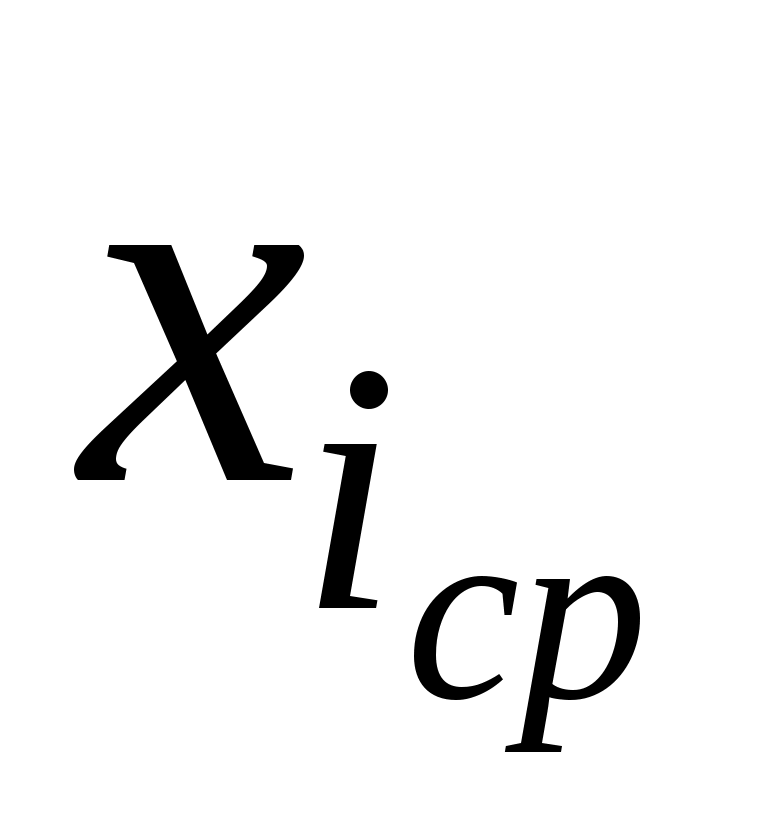
|
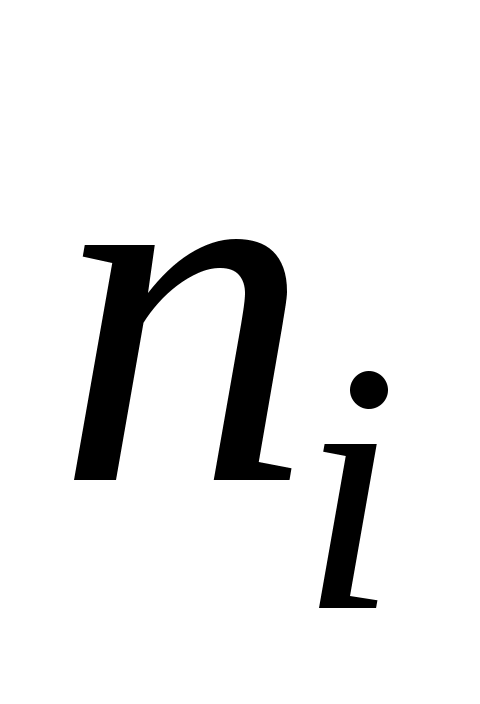
|
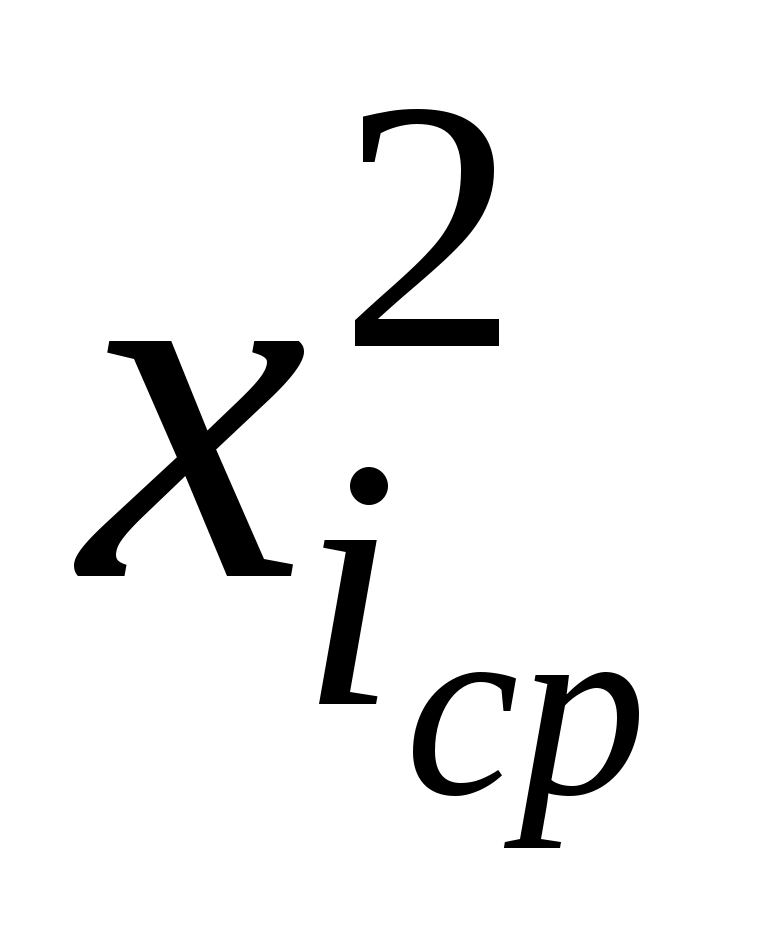
|
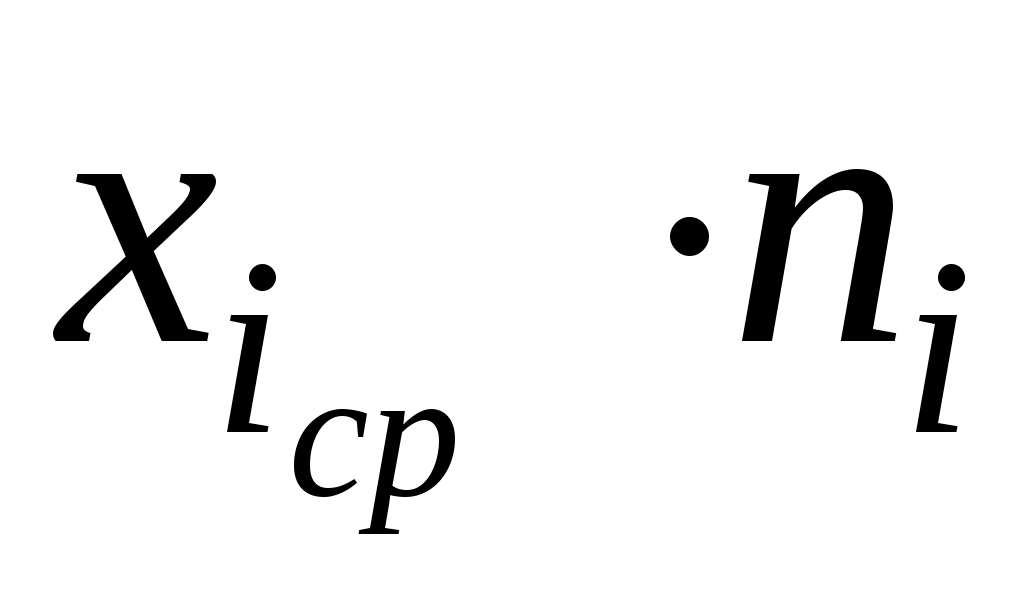
|
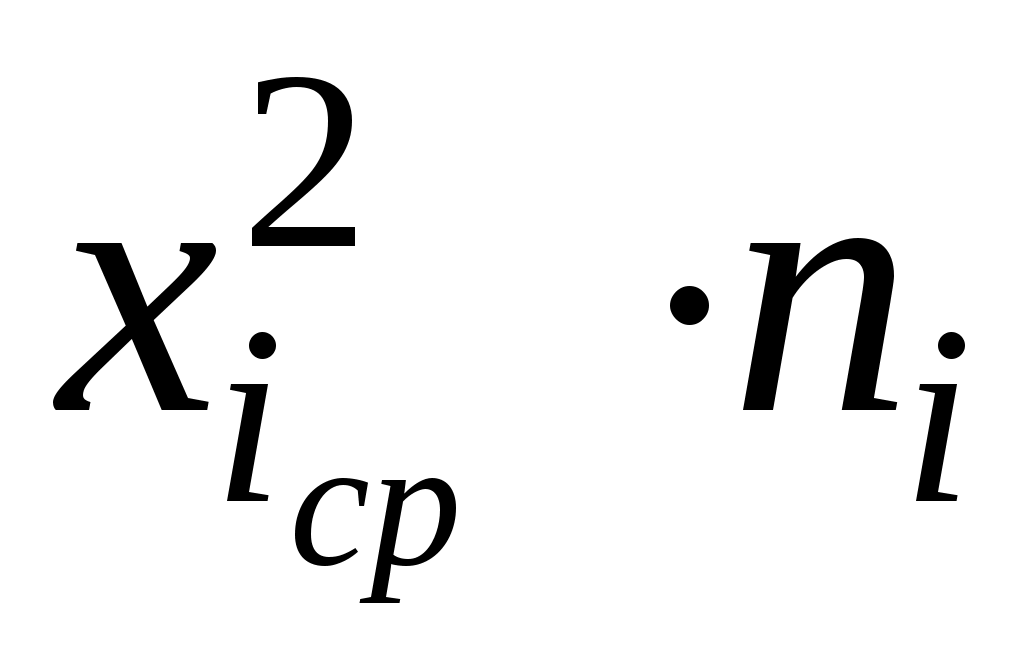
|
1
|
24,5-27,5
|
26
|
1
|
676
|
26
|
676
|
2
|
27,5-30,5
|
29
|
4
|
841
|
116
|
3364
|
3
|
30,5-33,5
|
32
|
13
|
1024
|
416
|
13312
|
4
|
33,5-36,5
|
35
|
23
|
1225
|
805
|
28175
|
5
|
36,5-39,5
|
38
|
22
|
1444
|
836
|
31768
|
6
|
39,5-42,5
|
41
|
30
|
1681
|
1230
|
50430
|
7
|
42,5-45,5
|
44
|
29
|
1936
|
1276
|
56144
|
8
|
45,5-48,5
|
47
|
16
|
2209
|
752
|
35344
|
9
|
48,5-51,5
|
50
|
10
|
2500
|
500
|
25000
|
10
|
51,5-54,5
|
53
|
2
|
2809
|
106
|
5618
|
∑
|
|
|
150
|
|
6063
|
249831
|
Находим : 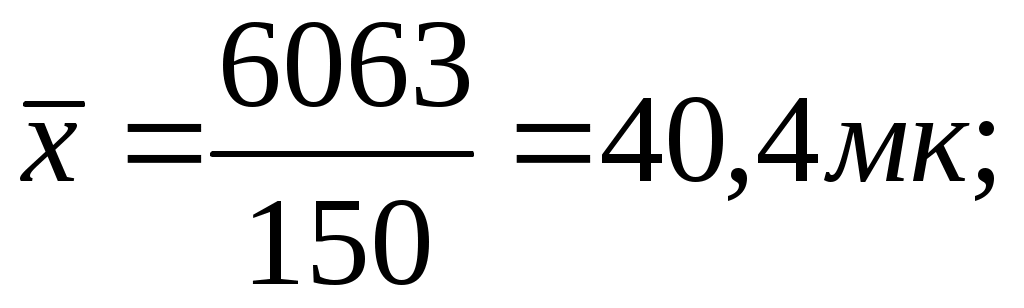 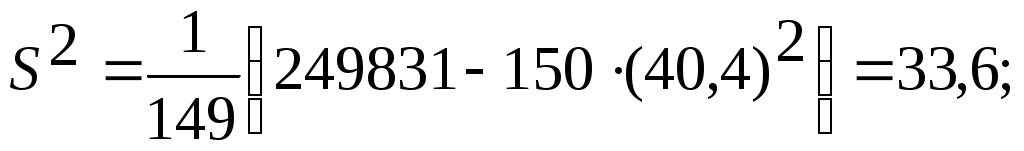 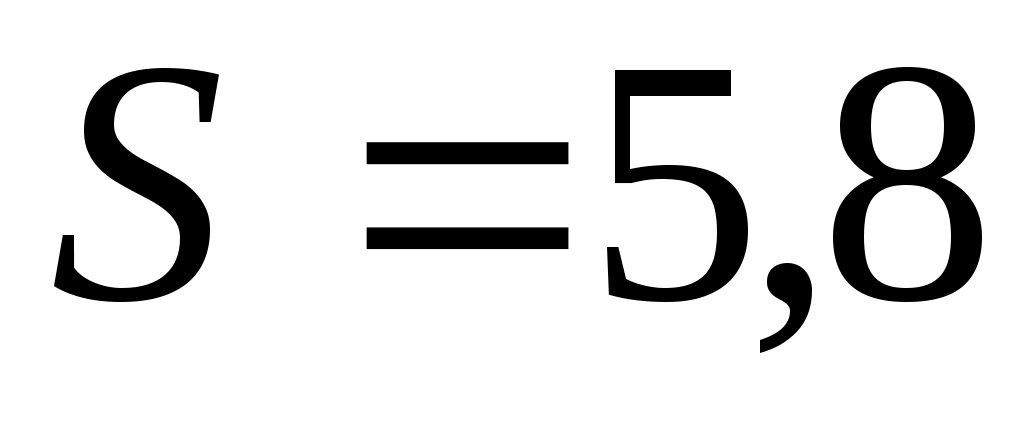 . .
3. Построим гистограмму частот (рис.4)
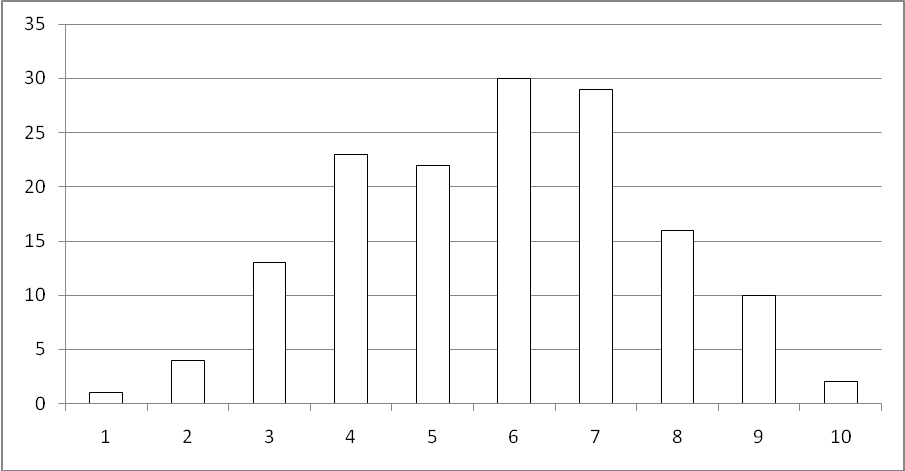
Рис.4
По виду гистограммы (рис.4) можно предположить, что исследуемый признак подчиняются нормальному закону распределения.
4. Найдем теоретические частоты 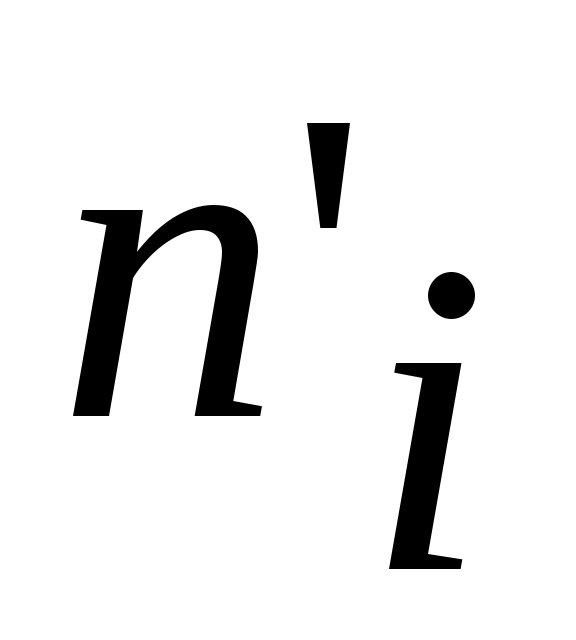 по формуле (3) при n=150, по формуле (3) при n=150, 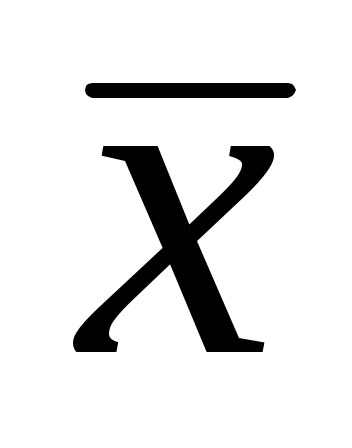 =40,4, S=5,8: =40,4, S=5,8:
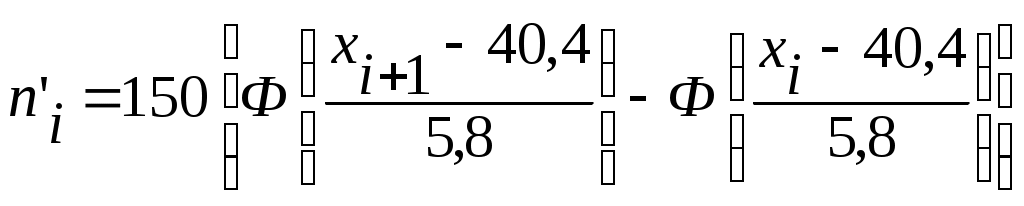 . .
В первом интервале левый конец изменим на 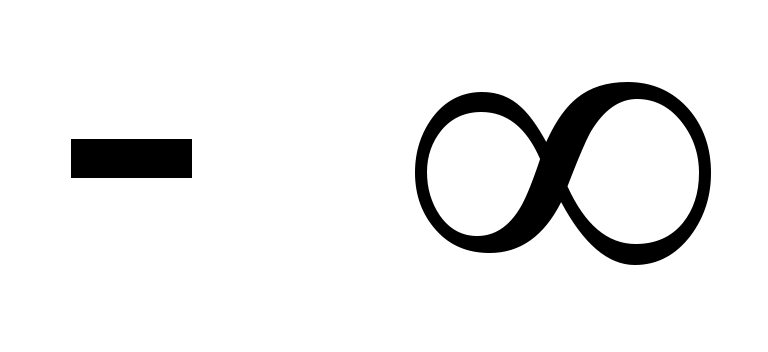 , а в последнем интервале - правый конец на , а в последнем интервале - правый конец на 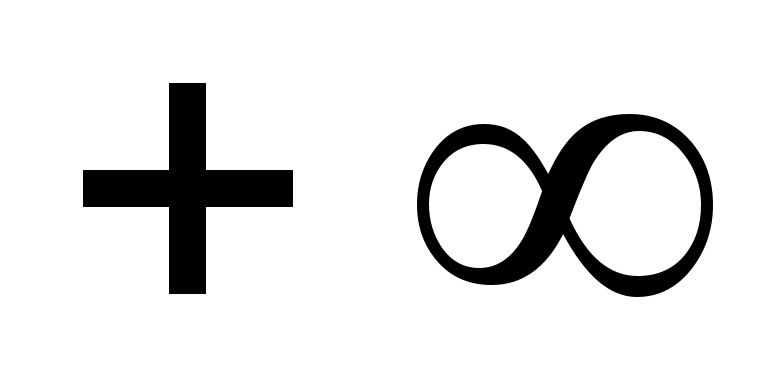 . Таким образом, первый интервал будет . Таким образом, первый интервал будет 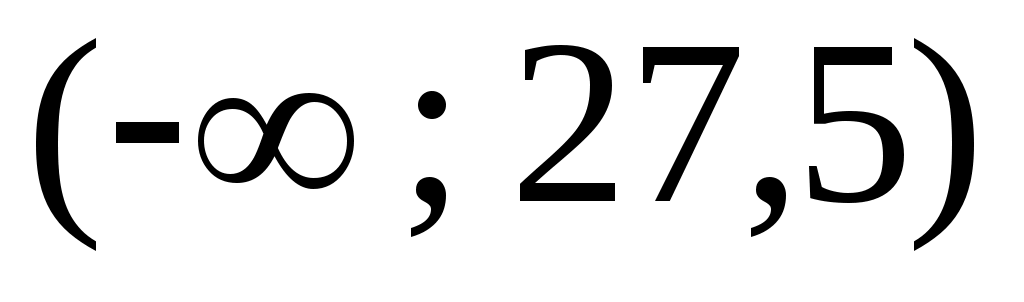 , а последний , а последний 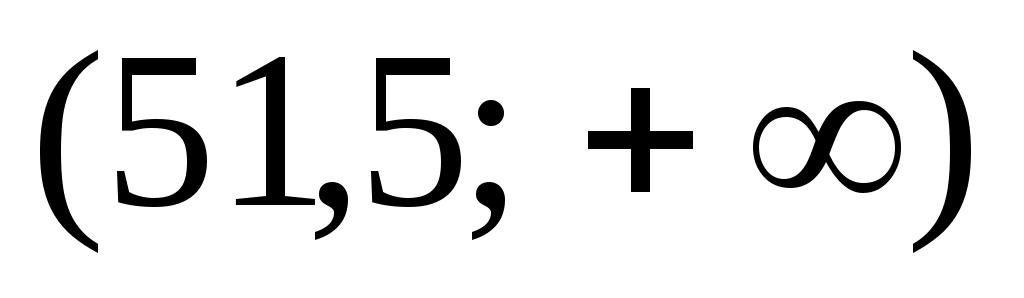 . Значения функции . Значения функции 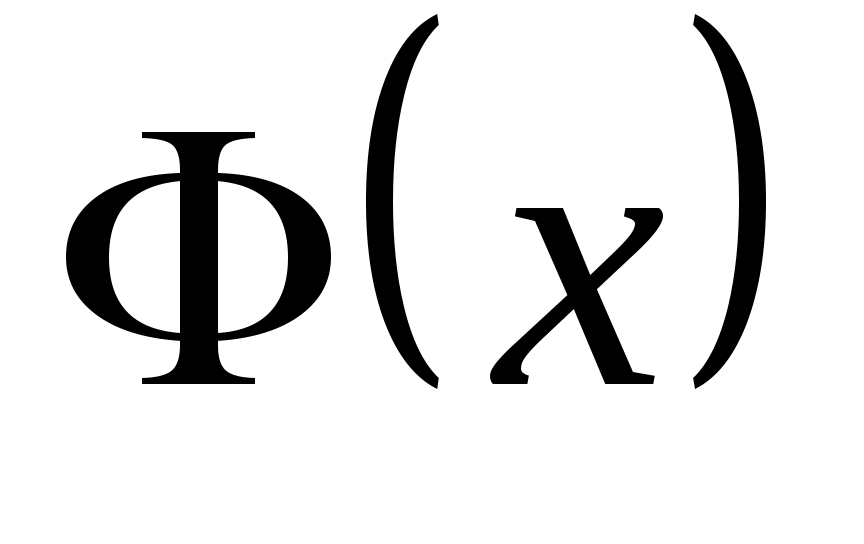 находятся из таблицы (приложение 7). При этом нужно учесть, что находятся из таблицы (приложение 7). При этом нужно учесть, что 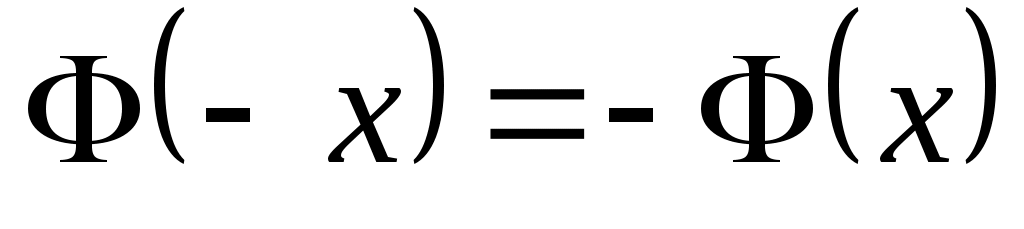 , и для , и для 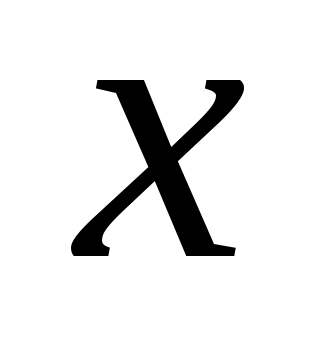 >5 значение >5 значение 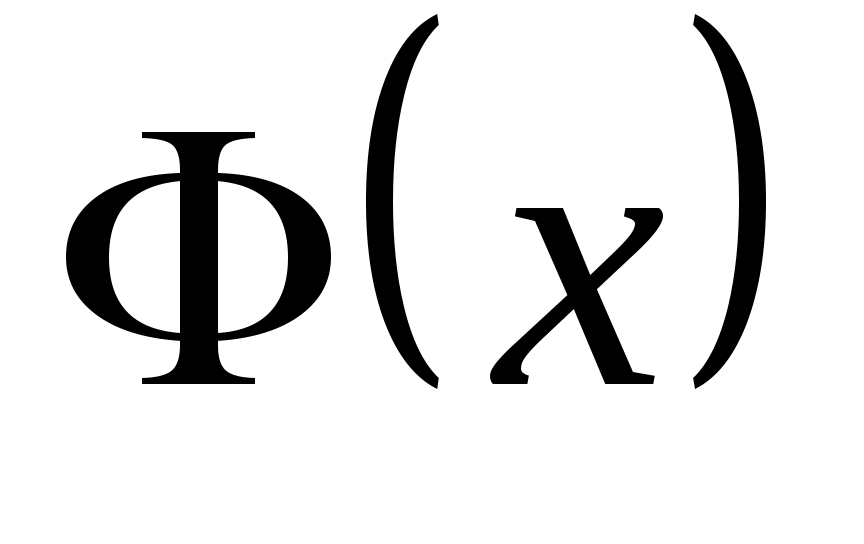 =0,5. =0,5.
Приведем пример расчета значения 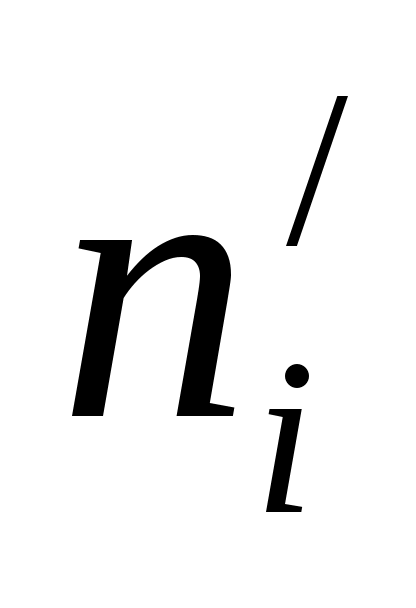 : :
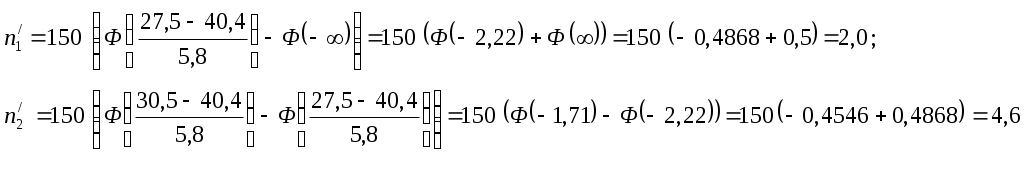
и так далее.
Расчёты для нахождения критерия 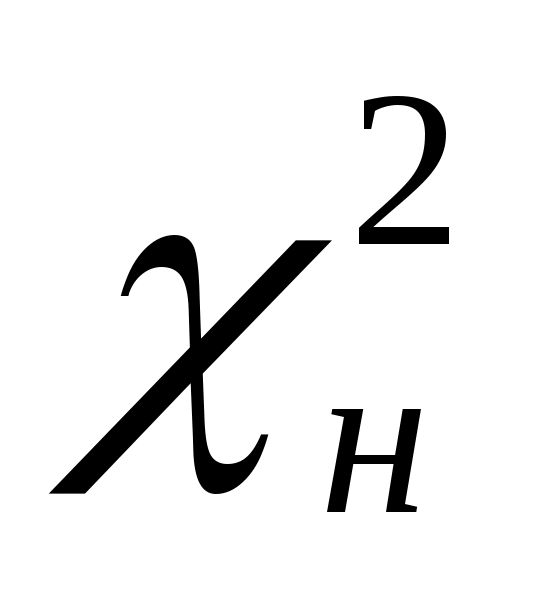 приведёны в таблице 3. приведёны в таблице 3.
Таблица 3
i
|
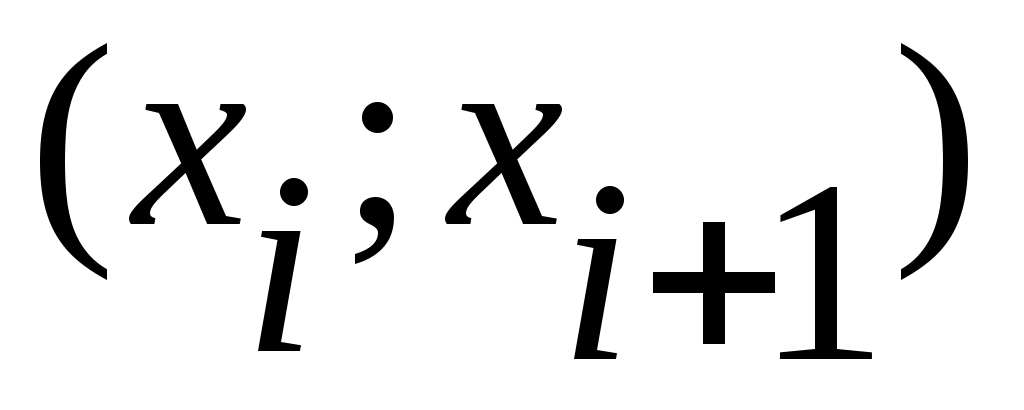
|
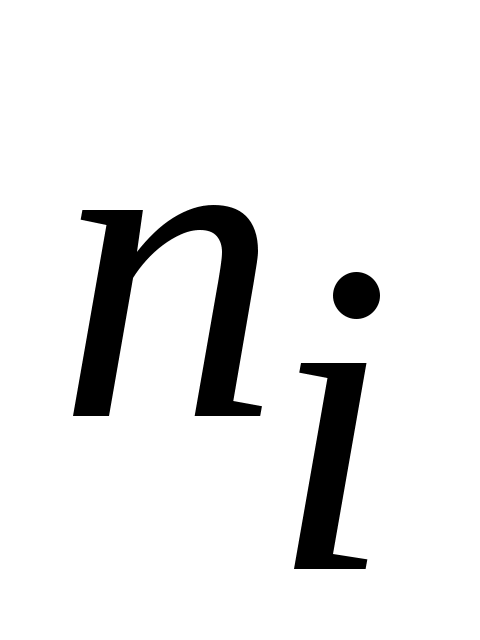
|
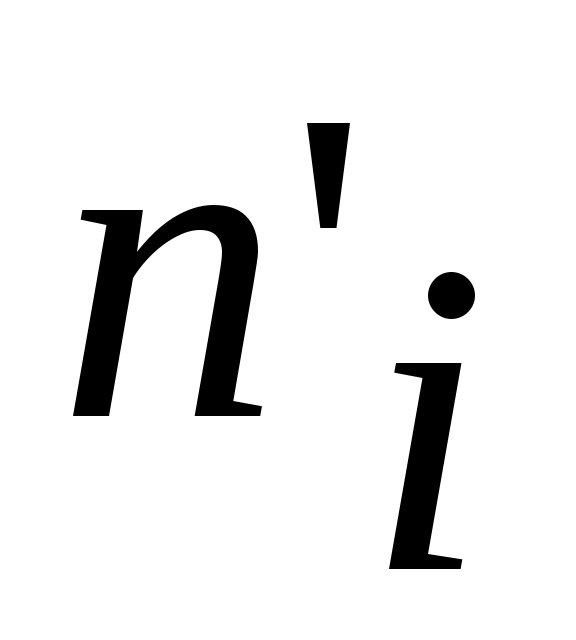
|
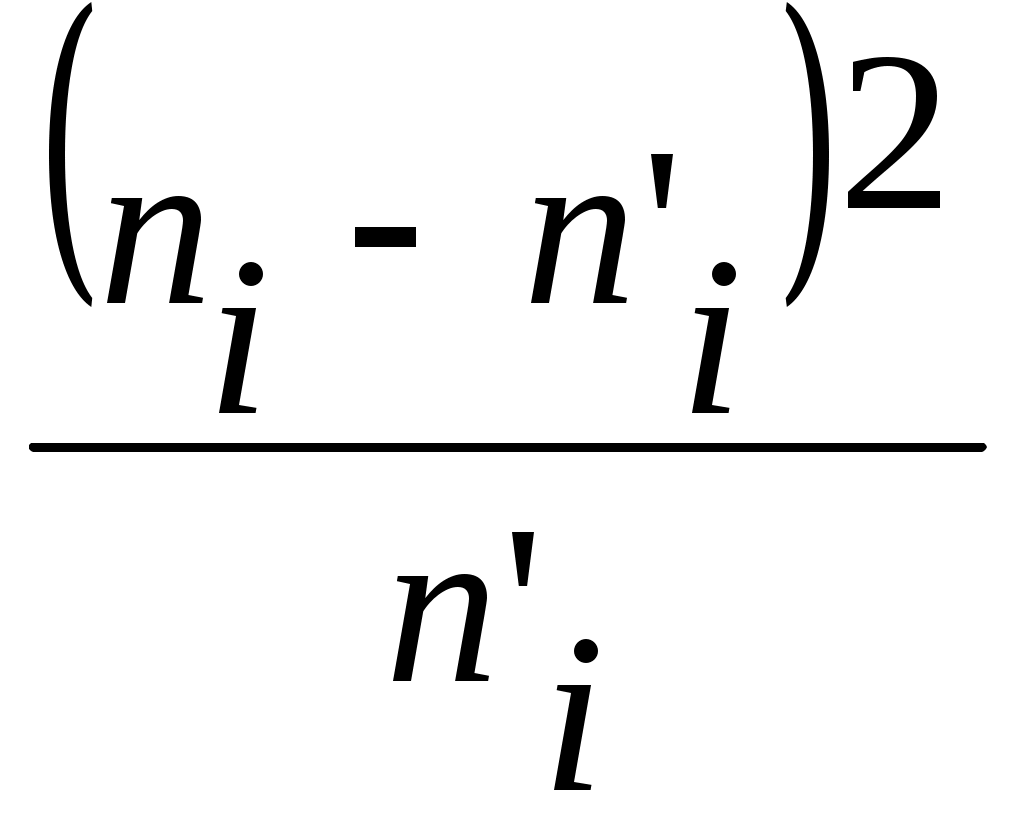
|
1
2
|
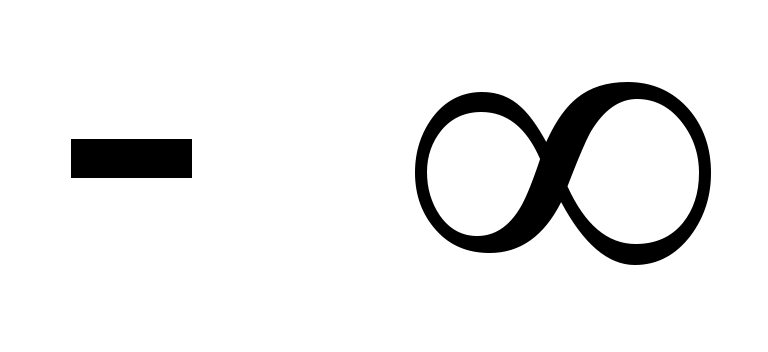 27,5 27,5
27,5 30,5
|
|
|
|
|
0,39
|
3
|
30,5 33,5
|
13
|
11
|
0,36
|
4
|
33,5 36,5
|
23
|
20,2
|
0,39
|
5
|
36,5 39,5
|
22
|
27,8
|
2,8
|
6
|
39,5 42,5
|
30
|
30,6
|
1,21
|
7
|
42,5 45,5
|
29
|
24,4
|
2,45
|
8
|
45,5 48,5
|
16
|
15,4
|
1,49
|
9
10
|
48,5 51,5
51,5 
|
|
|
|
|
|
0,00
|
∑
|
|
150
|
150
|
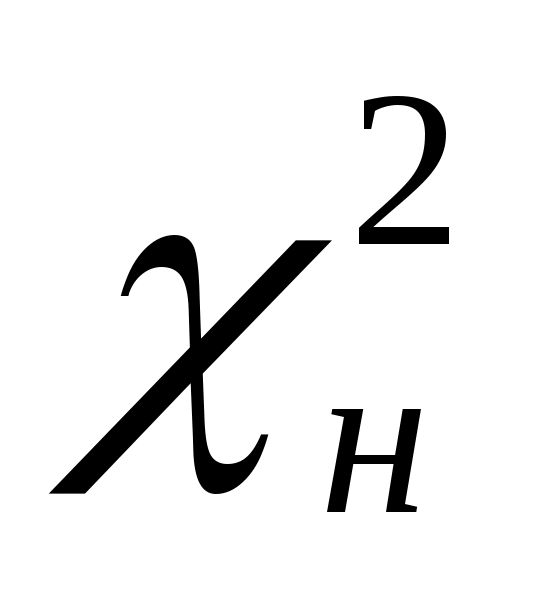 =3,26 =3,26
|
5. Число интервалов 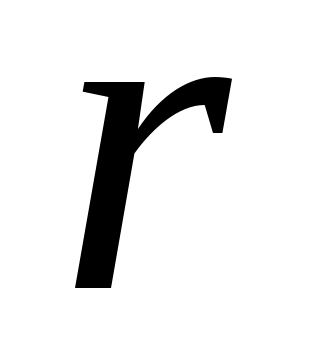 с учетом объединения частот равно 8. Проверку гипотезы о нормальном распределении проводим при уровне значимости с учетом объединения частот равно 8. Проверку гипотезы о нормальном распределении проводим при уровне значимости 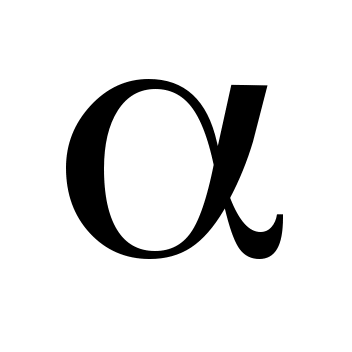 = 0,05 и числе степеней свободы, равном = 0,05 и числе степеней свободы, равном 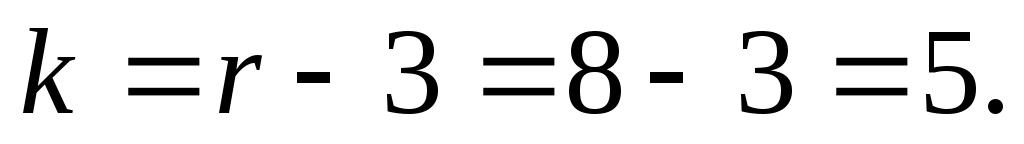 Из таблицы ( приложение 5) находим Из таблицы ( приложение 5) находим 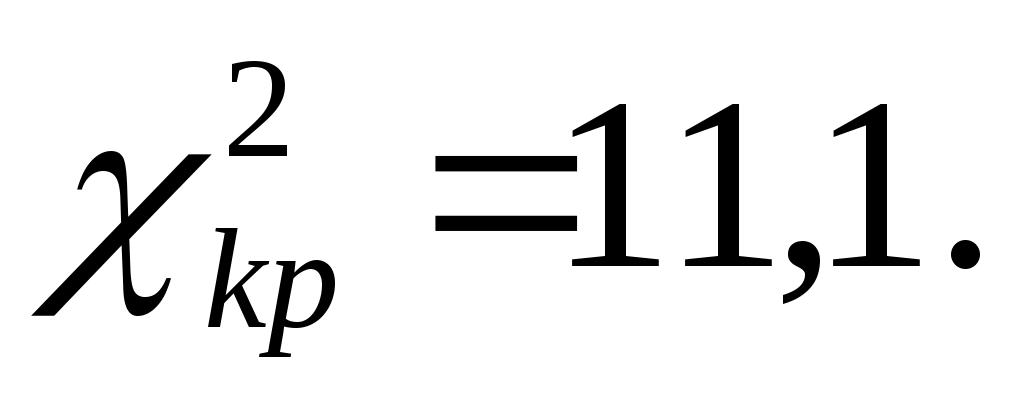
В нашем примере 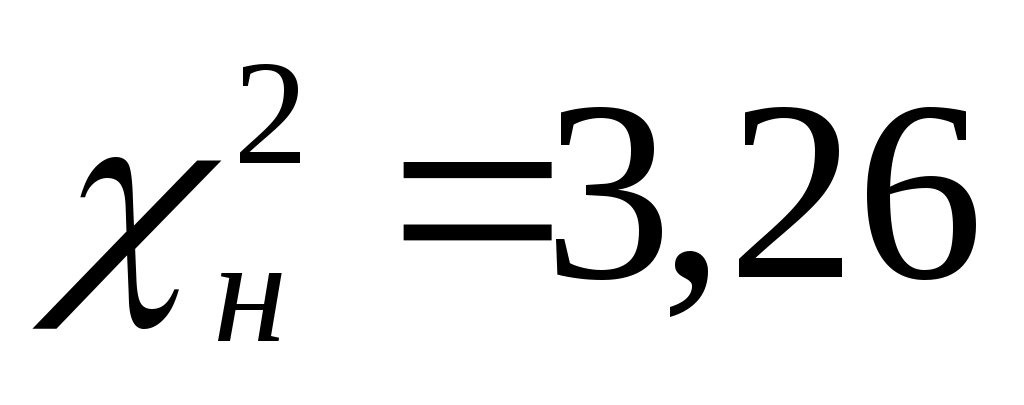 , т.е. , т.е. 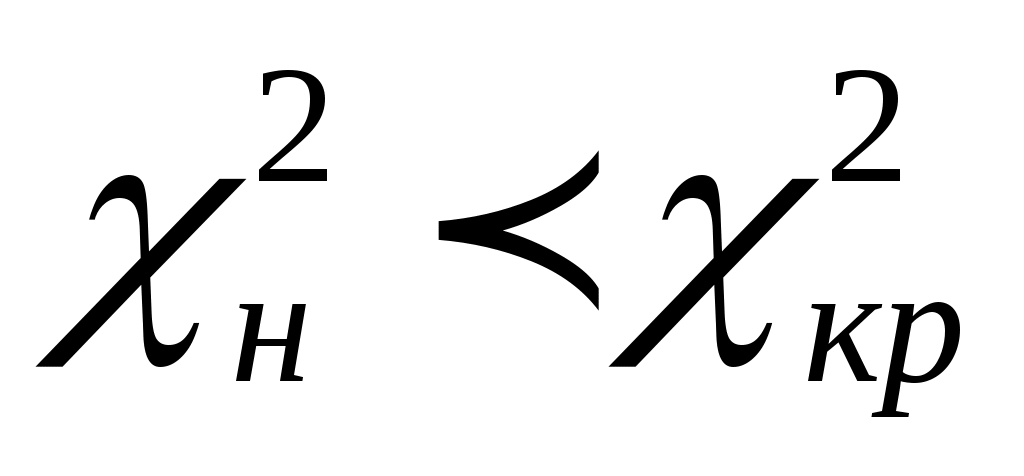 . .
Следовательно, опытные данные согласуются с нормальным законом распределения. На гистограмму наложим теоретическую кривую, полученную в соответствии с нормальным законом распределения.
6. Для построения нормальной кривой по опытным данным находим ординаты 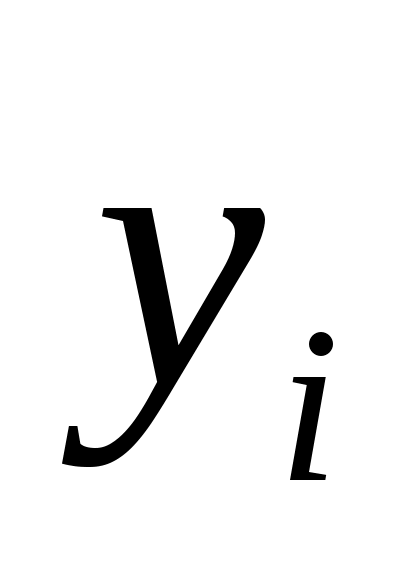 (выравнивающие частоты ) по формуле (выравнивающие частоты ) по формуле
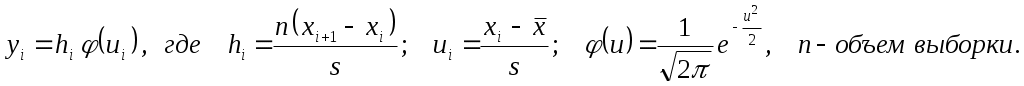
Значения функции 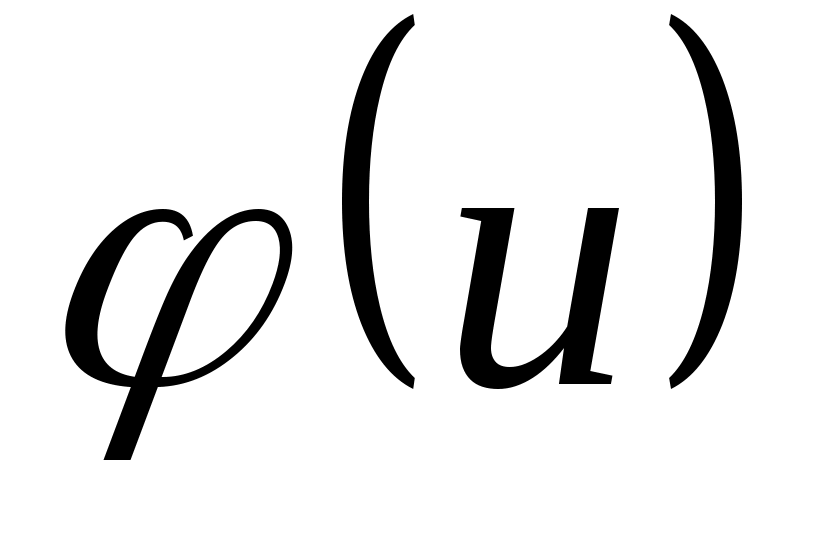 находим в таблице приложения 6. находим в таблице приложения 6.
Вычислим выравнивающие частоты для нашего примера. Имеем
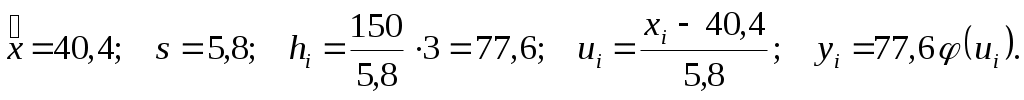
Результаты вычислений поместим в таблицу 4.
Таблица 4
-
i
|
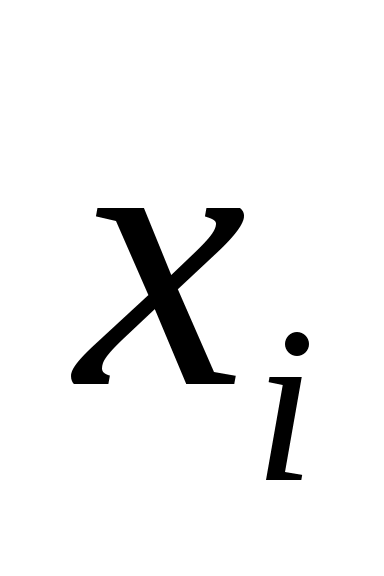
|
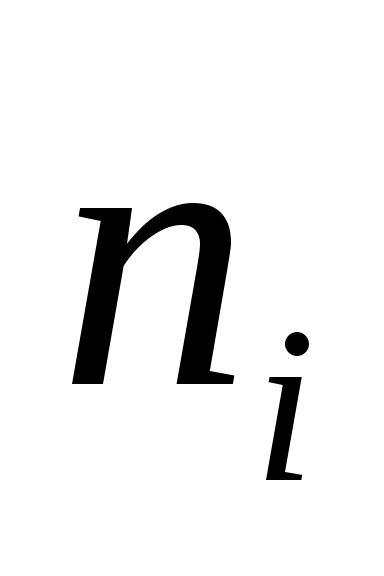
|
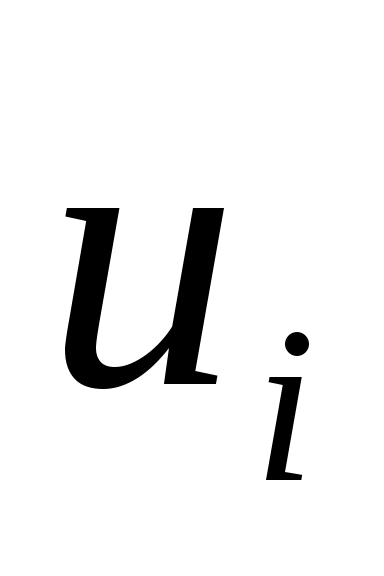
|
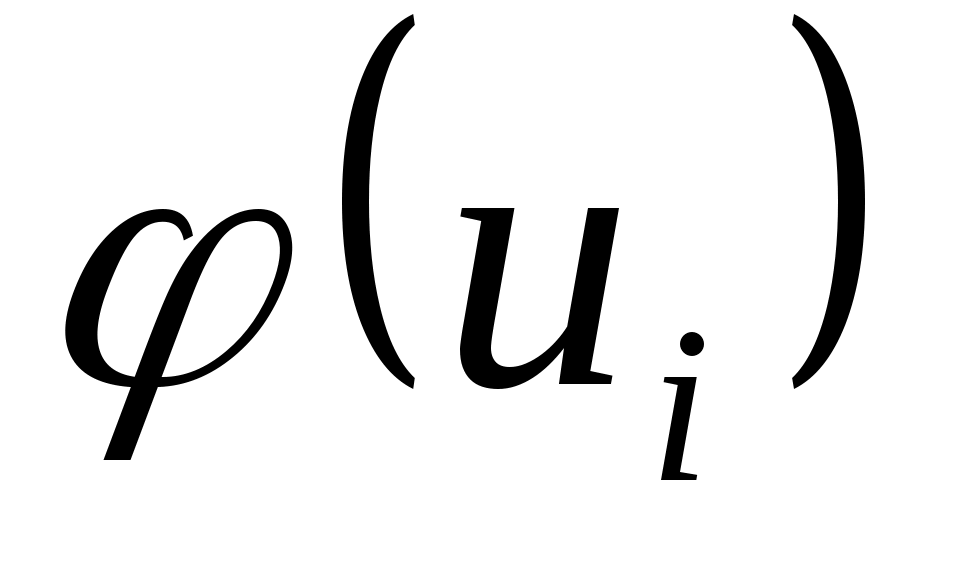
|
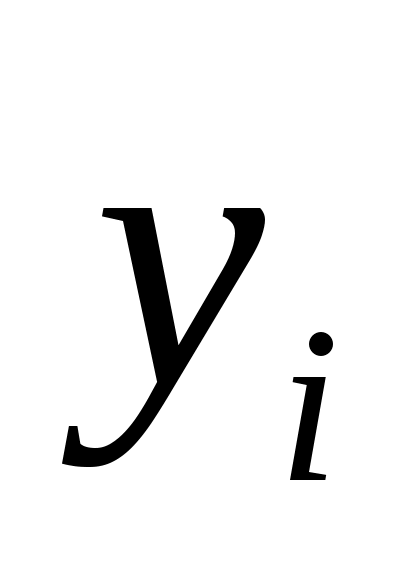
|
1
|
26
|
1
|
-2,48
|
0,02
|
1,6
|
2
|
29
|
4
|
-1,96
|
0,05
|
3,9
|
3
|
32
|
13
|
-1,45
|
0,14
|
10,8
|
4
|
35
|
23
|
-0,94
|
0,26
|
20,2
|
5
|
38
|
22
|
-0,41
|
0,37
|
28,7
|
6
|
41
|
30
|
0,10
|
0,39
|
30,3
|
7
|
44
|
29
|
0,62
|
0,33
|
25,6
|
8
|
47
|
16
|
1,14
|
0,21
|
16,3
|
9
|
50
|
10
|
1,66
|
0,09
|
7,0
|
10
|
53
|
2
|
2,17
|
0,04
|
3,1
|
В прямоугольной системе координат строим точки 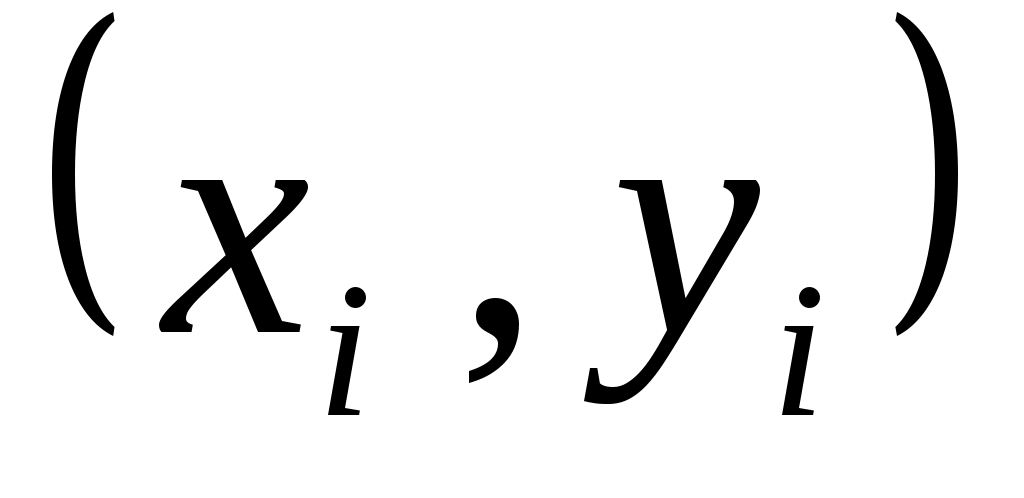 и соединяем их плавной кривой (рис.5). Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что исследуемый признак распределен нормально. и соединяем их плавной кривой (рис.5). Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что исследуемый признак распределен нормально.

Рис.5
|
|
|
 Скачать 1.49 Mb.
Скачать 1.49 Mb.

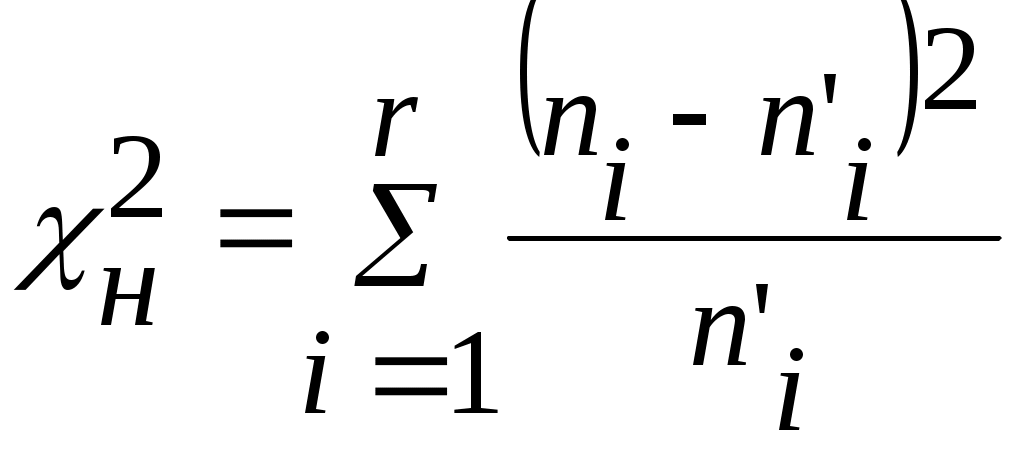 , (1)
, (1)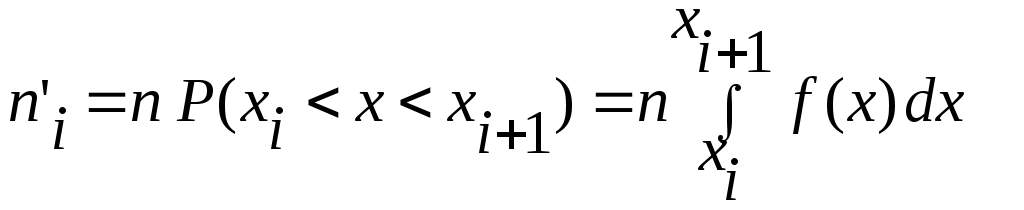 , (2)
, (2)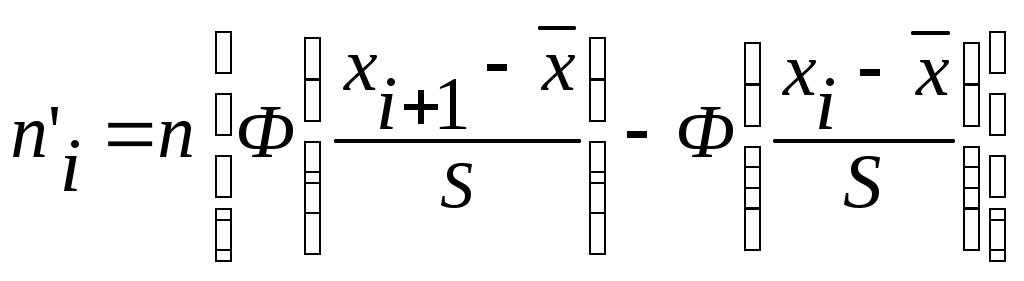 , (3)
, (3)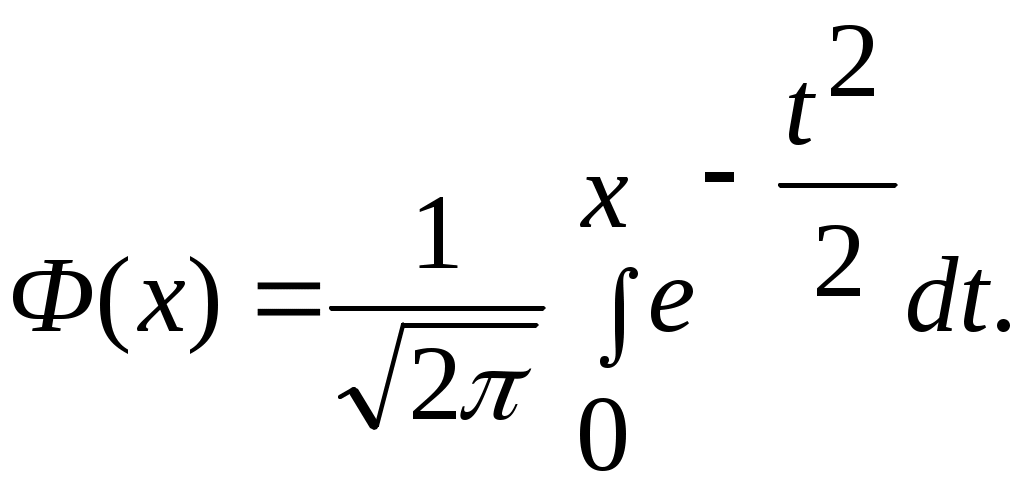 (4)
(4) . (5)
. (5)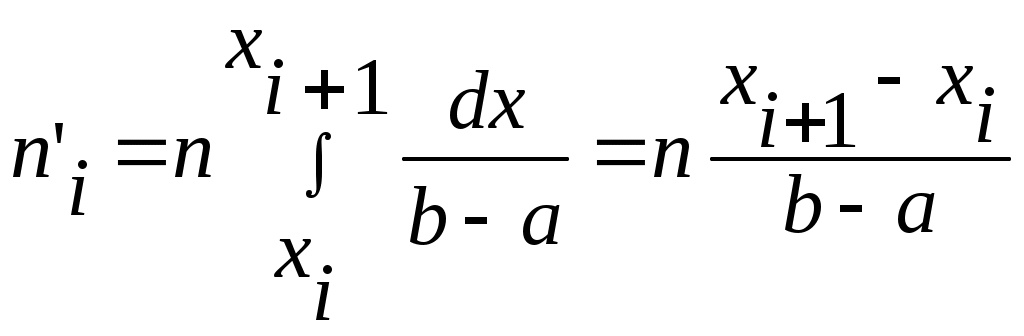 . (6)
. (6)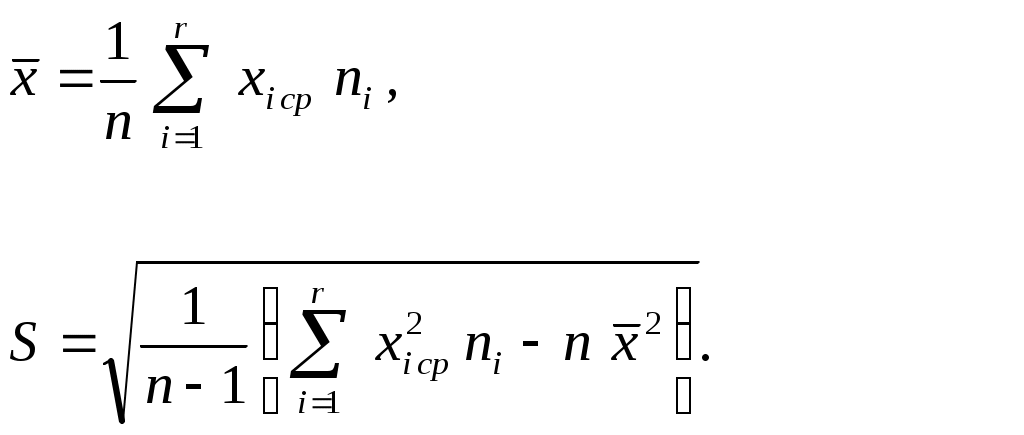 (9)
(9)
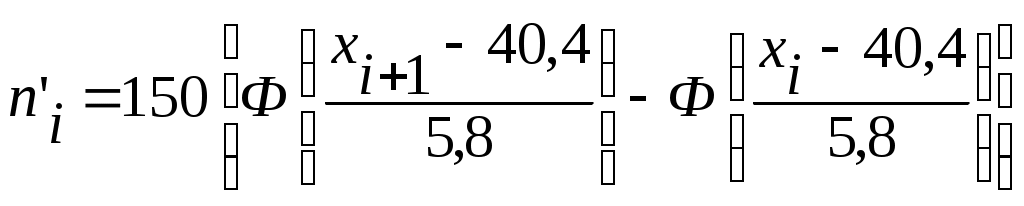 .
.