теория вероятности. Теория. Решение задач типового варианта расчетной работы Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять

• Название: Решение задач типового варианта расчетной работы Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять
• Анкор: теория вероятности
• Дата: 16.01.2022
• Размер: 1.49 Mb.
• Имя файла: Теория.doc
• Тип: Решение; #332464
• страница: 4 из 7

2.3.3 Проверка гипотезы равномерного распределения
Задано эмпирическое распределение непрерывной случайной величины в виде последовательности интервалов и соответствующих им частот , причем (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина X распределена равномерно.

Для того чтобы проверить гипотезу о равномерном распределении 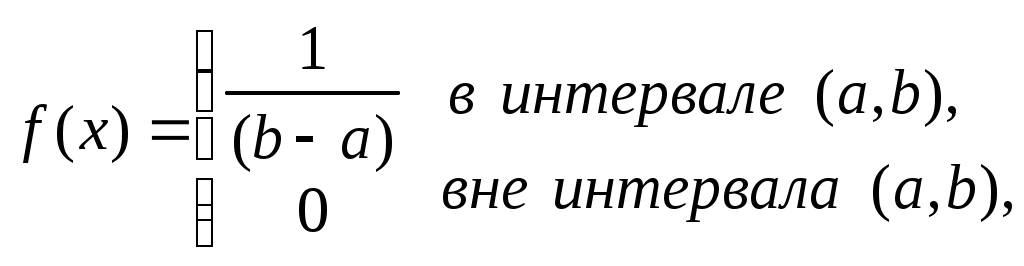, т.е. по закону



надо:

1. 
   Оценить параметры и - концы интервала, в котором наблюдались возможные значения , по формулам (через и обозначены оценки параметров)
   

.

2. 
   Найти плотность вероятности предполагаемого распределения
   

.

3. 
   Найти теоретические частоты:
   

.

4. 
   Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы , где - число интервалов, на которые разбита выборка.
   

Пример 4. Произведено n=200 испытаний, в результате каждого из которых событие А появлялось в различные моменты времени. В итого было получено эмпирическое распределение, приведенное в табл.10 (в первой строке указаны интервалы времени в минутах, во второй – соответствующие частоты, т.е. число появления А в интервале). Требуется при уровне значимости 0,05 проверить гипотезу о том, что время появления событий распределено равномерно.
Таблица 10

интервал	2-4	4-6	6-8	8-10	10-12	12-14	14-16	16-18	18-20	20-22
частота	21	16	15	26	22	14	21	22	18	25

Решение

1. Построим гистограмму частот (рис.8)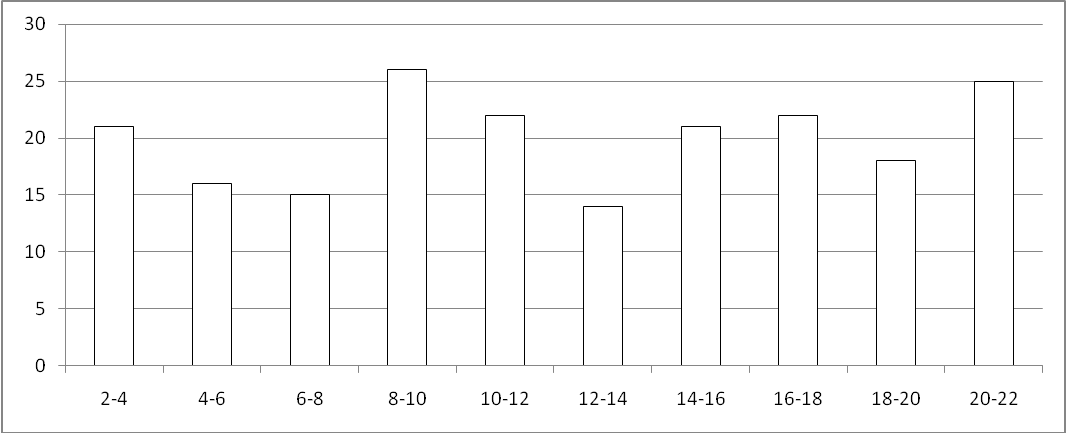


Рис. 8

По виду гистограммы частоты отклоняются от некоторой прямой. Предположим, что имеем равномерное распределение.

2. Для вычисления выборочной средней и выборочного среднего квадратического отклонения примем середины интервалов в качестве вариант (наблюдаемых значений X). В итоге получим эмпирическое распределение равноотстоящих вариант (табл.11):

Таблица 11

i
1	2 - 4	3	21	9	63	189
2	4 - 6	5	16	25	80	400
3	6 - 8	7	15	49	105	735
4	8 - 10	9	26	81	234	2106
5	10 - 12	11	22	121	242	2662
6	12 - 14	13	14	169	182	2366
7	14 - 16	15	21	225	315	4725
8	16 - 18	17	22	289	374	6358
9	18 - 20	19	18	361	342	6498
10	20 - 22	21	25	441	525	11025
∑			200		2462	37064

Найдем: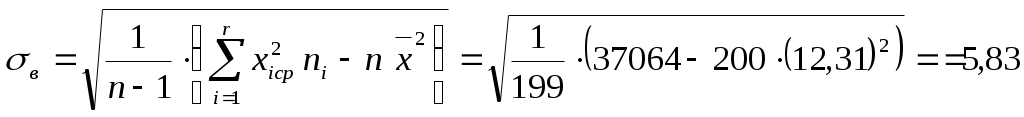




Найдем оценки параметров и равномерного распределения по формулам: ,

получим

.
3. Найдем плотность предполагаемого равномерного распределения:

3. 
   Найдем теоретические частоты:
   

Длины третьего - девятого интервалов равны длине второго интервала, поэтому теоретические частоты, соответствующие этим интервалам и теоретическая частота второго интервала одинаковы, т.е.

3. 
   Сравним эмпирические и теоретические частоты с помощью критерия Пирсона, для этого составим таблицу 12.
   

Таблица 12

i
1	21	17,8	10,24	0,58
2	16	20	16	0,80
3	15	20	25	1,25
4	26	20	36	1,80
5	22	20	4	0,20
6	14	20	36	1,80
7	21	20	1	0,05
8	22	20	4	0,20
9	18	20	4	0,20
10	25	24	1	0,04
∑	200