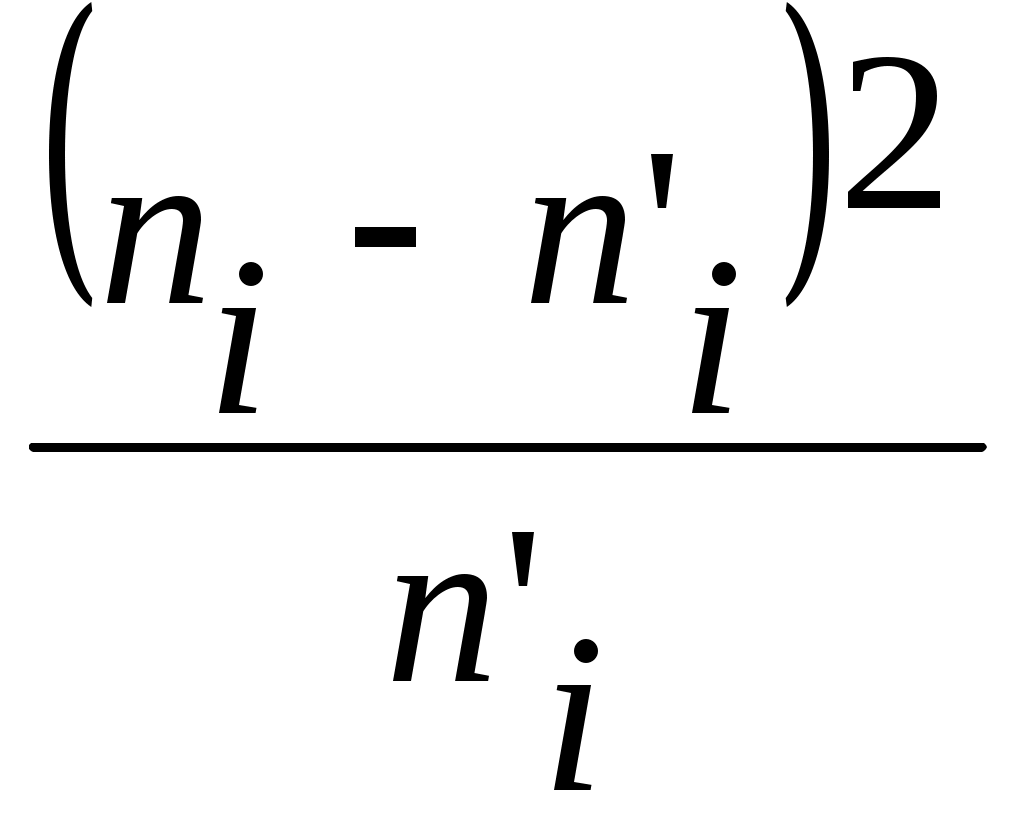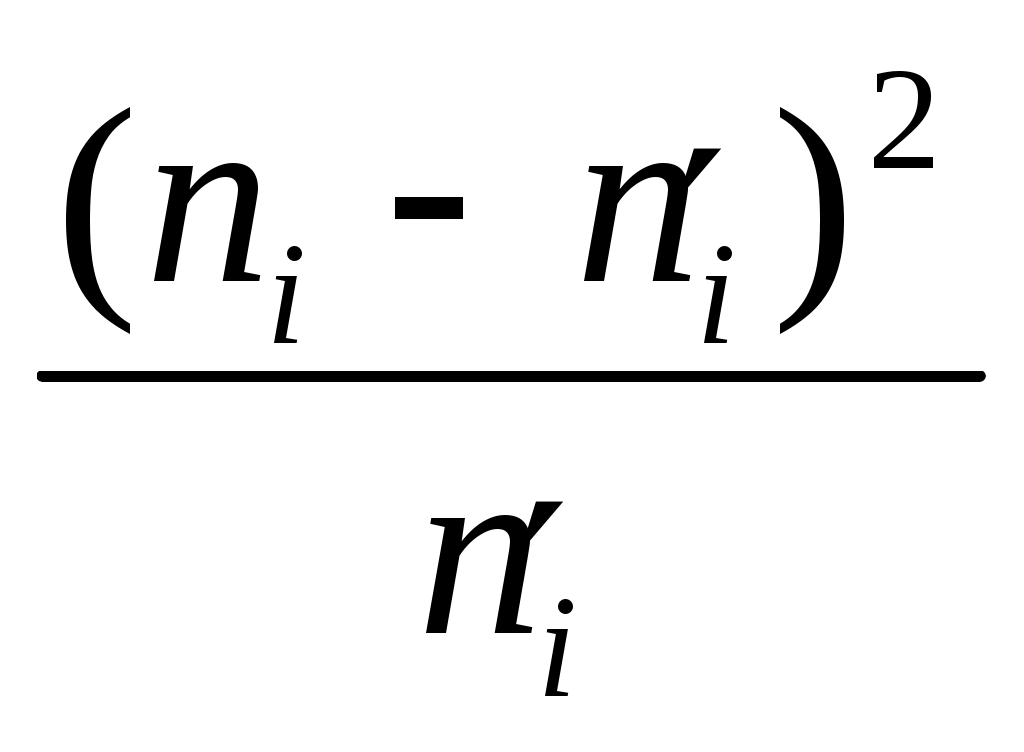теория вероятности. Теория. Решение задач типового варианта расчетной работы Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять

• Название: Решение задач типового варианта расчетной работы Задача Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять
• Анкор: теория вероятности
• Дата: 16.01.2022
• Размер: 1.49 Mb.
• Имя файла: Теория.doc
• Тип: Решение; #332464
• страница: 3 из 7

Пример 2 Эмпирическое распределение выборки объема n=100 приведено в таблице 5.

Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х c эмпирическим распределением выборки .

Таблица 5

i			i
1	3 - 8	6	5	23 -28	16
2	8 - 13	8	6	28 -33	8
3	13 - 18	15	7	33 -38	7
4	18 - 23	40

Решение

1. Построим гистограмму(рис.6)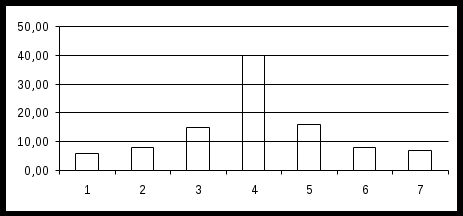


Рис.6

По виду гистограммы (рис.6) можно предположить, что исследуемый признак подчиняются нормальному закону распределения.

2. Для каждого частичного интервала найдем :

Вычислим значения и S по формулам (9); расчеты поместим в таблицу (табл.6).

Таблица 6

i
1	3 - 8	5,5	6	30,25	36	181,5
2	8 -13	10,5	8	110,25	84	882
3	13 -18	15,5	15	240,25	232,5	3603,75
4	18 -23	20,5	40	420,25	820	16810
5	23 -28	25,5	16	650,25	480	10404
6	28 -33	30,5	8	777,25	244	7442
7	33 -38	35,5	7	1260,25	248,5	8821,75
∑			100		2070	48145

Находим: .

3. Найдем теоретические частоты 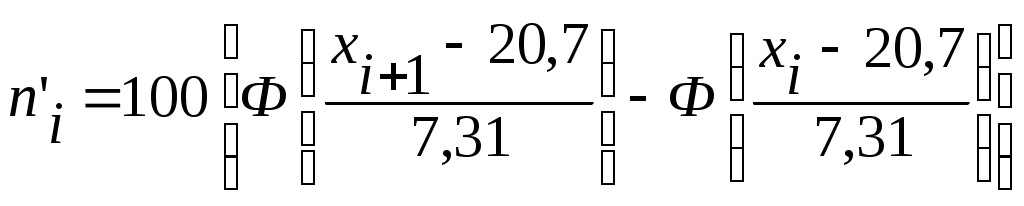по формуле (3) при n=100; =20,7; S=7,31:

.

Расчёты для нахождения критерия приведёны в таблице 7.

Таблица 7

i
1	- 8	6	4,09	0,89
2	8 - 13	8	10,60	0,64
3	13 - 18	15	20,88	1,66
4	18 - 23	40	26,60	6,75
5	23 - 28	16	21,96	1,62
6	28 - 33	8	11,22	0,92
7	33 -	7	4,65	1,19
∑		100		=13,67

4. Число интервалов равно 7. Проверку гипотезы о нормальном распределении проводим при уровне значимости = 0,05 и числе степеней свободы, равном Из таблицы ( приложение 5) находим .

В нашем примере , т.е. > . Следовательно, опытные данные не согласуются с нормальным законом распределения и гипотеза о нормальном распределении отвергается.
2.3.2 Проверка гипотезы о показательном распределении генеральной совокупности.

Задано эмпирическое распределение непрерывной случайной величины X в виде последовательности интервалов ( ) и соответствующих им частот , причем (объем выборки). Требуется, используя критерий Пирсона, проверить гипотезу о том, что случайная величина X имеет показательное распределение.

Для того чтобы при уровне значимости α проверить гипотезу о том, что непрерывная случайная величина распределена по показательному закону, надо:

1. Найти по заданному эмпирическому распределению выборочную среднюю , приняв в качестве «представителя» i-го интервала его середину .

2. Принять в качестве оценки параметра λ показательного распределения величину, обратную выборочной средней: .

4. Вычислить теоретические частоты по формуле (5).

5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы , где – число интервалов выборки c учетом объединения малочисленных частот.
Пример 3. В результате испытания 200 элементов на длительность работы в часах получено эмпирическое распределение, приведенное в таблице 8. Во второй строке таблицы указаны интервалы времени в часах, в третьей – частоты, т.е. количество элементов, проработавших время в пределах соответствующего интервала.

Таблица 8

i	1	2	3	4	5	6
	0-5	5-10	10-15	15-20	20-25	25-30
	133	45	15	4	2	1

Решение.

1. Построим гистограмму частот (рис.7).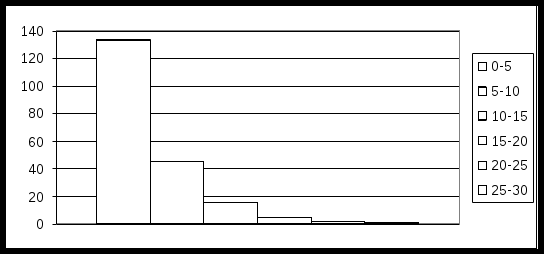



Рис. 7

Предполагаемое распределение – показательное.

2. Найдем среднее время работы для всех элементов (в качестве среднего времени работы одного элемента примем середину интервала, которому принадлежит элемент):



3.Найдем оценку параметра предполагаемого показательного распределения:



Таким образом, плотность предполагаемого показательного распределения имеет вид .

4. Найдем вероятности попадания случайной величины X в каждый из интервалов по формуле :













5. Найдем теоретические частоты по формуле (5): _, где - вероятность попадания случайной величины X в i-ый интервал. Получаем:



6. Сравним эмпирические и теоретические частоты с помощью критерия Пирсона. Составим расчетную таблицу 9. Для упрощения вычислений объединим интервалы 4, 5, и 6 малочисленных частот в один интервал, получим интервал (15;30).

Объединим также малочисленные частоты (4+2+1=7) и соответствующие им теоретические частоты (6,30+2,32+0,84=9,46).
Таблица 9

1	133	126,42	6,58	43,2964	0,3425
2	45	46,52	-1,52	2,3104	0,0497
3	15	17,10	-2,10	4,4100	0,2579
4	7	9,46	-2,46	6,0516	0,6397
Σ

Из таблицы критических точек распределения χ², по уровню значимости α=0,05 и числу степеней свободы находим =6,0.

Так как < , то нет оснований отвергнуть гипотезу о распределении X по показательному закону. Другими словами, данные наблюдений согласуются с этой гипотезой.