интеграция. Интеграция. Решение задач в рамках межпредметной интеграции на уроках математики Данаева Анна Донатовна учитель математики мбоу Ясногорская сош, Кемеровский район Кемерово 2018 год Оглавление Введение Глава 1

• Название: Решение задач в рамках межпредметной интеграции на уроках математики Данаева Анна Донатовна учитель математики мбоу Ясногорская сош, Кемеровский район Кемерово 2018 год Оглавление Введение Глава 1
• Анкор: интеграция
• Дата: 10.04.2022
• Размер: 0.73 Mb.
• Имя файла: Интеграция.docx
• Тип: Решение; #458331
• страница: 3 из 5

Пример 1

- |-8| - |-5 | (Из модуля минус восьми вычесть модуль минус пяти).

- |28,52|:|-2,3| (Модуль двадцати восьми целых пятидесяти двух сотых разделить на модуль минус двух целых трех десятых).

Можно предложить учителю русского языка дать подобные задания на его уроках. Время изучения материала совпадает. Возможно, дать общее домашнее задание по русскому языку и математике, а затем оценить отдельно по каждому предмету. К тому же учащиеся оценят необычность подобного задания, что вызовет дополнительный интерес к нему.

Очень часто ученики в существительном «длина» пишут удвоенное «н». Имеет смысл разъяснить, что существуют слова «длина» и «длинна», но первое – это имя существительное и означает величину предмета, второе – краткое прилагательное, обозначающее свойство предмета (например, «дорога длинна»).

2.2.2. Математика и физика

Связи между науками математики и физики многообразны и постоянны.

Математика как наука сформировалась первой, но по мере развития физических знаний математические методы находили все большее применение в физических исследованиях. Взаимосвязи математики и физики определяются, прежде всего, наличием общей предметной области, изучаемой ими, хотя и с различных точек зрения. Взаимосвязь математики и физики выражается во взаимодействии их идей и методов. Эти связи можно условно разделить на три вида:

– физика ставит задачи и создает необходимые для решения математические идеи и методы, которые в дальнейшем служат базой для развития математической теории;

– развитая математическая теория с ее идеями и математическим аппаратом используется для анализа физических явлений, что часто приводит к новой физической теории, которая в свою очередь приводит к развитию физической картины мира и возникновению новых физических проблем;

– развитие физической теории опирается на имеющийся определенный математический аппарат, но последний совершенствуется и развивается по мере его использования в физике.

Именно поэтому, в системе школьных учебных предметов наибольшую связь, имеют математика и физика. Связь здесь состоит в том, что в целях формирования общеучебных умений и навыков при решении задач важно знакомить учащихся с общими методами и подходами (координатный, алгоритмический) к анализу задачи, ее решению и оформлению [25,26]. Это должно отражать единство требований к решению задач по математике, физике и химии. По мнению Ю.И. Дика, при решении задач, как по математике, так и по физике, учащиеся могут проводить самоконтроль через: оценку ответа задачи на реальность; проверку правильности записи формул, формул по размерности; правильность осуществленных преобразований, вычислений; сравнение этапов решения задачи с подобной (решенной ранее и разобранной в учебнике, с предлагаемым учителем образцом); сравнение содержания и последовательности, выполненных при решении задач действий с алгоритмом (составленным для решения задач) [13] . На уроках химии решаются задачи, при этом очень часто приходится иметь дело с решением уравнений, выявлением прямой и обратной пропорциональной зависимости. Важно поэтому обеспечить единство подходов, о которых говорилось выше, использования на уроках химии тех алгоритмов, которые учащиеся уже применяли на уроках математики.

Понятие функциональной зависимости является одним из ведущих в математике и очень часто используется на уроках физики. Первое знакомство с графиками ученики получают на уроках математики в 6 классе. При этом они учатся строить графики движения пешехода, поезда, температуры (по таблице), находить по графику значение одной переменной, если задано значение другой переменной. Ярким примером пропедевтики физических знаний является задача. При вычерчивании графиков на уроках физики учащиеся применяют знания по математике и развивают представления о функциональной зависимости. Надо обратить внимание на то, что при рассмотрении физических закономерностей широко используют графики, причем координатные оси обозначают символами тех физических величин, зависимость между которыми исследуется графиком [8].

Иногда учащиеся отождествляют график с траекторией движения.

Чтобы избежать такой ошибки, которая встречается в знаниях учащихся не только в 7 классе, но и в 9 классе, следует учить их читать и анализировать графики движения [20]. Большие возможности для понимания функциональных зависимостей дает материал алгебры и физики в 7 классе [31]. Здесь изучение темы «Движение и силы» в курсе физики несколько опережает изучение темы «Функция» в курсе алгебры, поэтому на уроках математики естественно использовать знания, полученные на уроках физики.

Вместе с тем, в дополнение к тем задачам по физике, которые даны в учебнике А.В. Перышкина, учащимся можно предложить рассмотреть задачу такого содержания:

Пример 1

- Велосипедист едет равномерно со скоростью 27 км/ч, его обгоняет мотоциклист, едущий со скоростью 72 км/ч. Построить график пути и скорости движения велосипедиста и мотоциклиста. Сравнить их [26] .

На уроках алгебры в 7 классе дается понятие прямой, обратной пропорциональной линейной зависимостей. Использование физических задач на нахождение массы тела по его плотности и объему, силы давления по давлению и площади опоры позволят на уроках математики показать практическую ценность изучаемого материала [20].

При изучении темы «Скорость прямолинейного равноускоренного движения. График скорости» подчеркивается, что зависимость скорости от времени в этом случае является линейной. И от того, насколько ученики усвоили этот материал в курсе математики, зависит успешность усвоения материала по физике [25].

Дальнейшее изучение и углубление понятия функциональной зависимости происходит в 8 классе при изучении квадратичной функции и играет перспективную роль при изучении равноускоренного движения в курсе физики 9 класса. Поэтому при решении задач по физике по этой теме важно использовать этот же алгоритм решения квадратных уравнений, что и в курсе алгебры, использовать возможности теоремы Виета. Для устранения путаницы в умах учащихся между траекторией движения и графиком движения, а также для повторения метода графического решения уравнений к задачам в упражнении 7 можно добавить следующий пример:

Пример 2

- Автомобиль, имея начальную скорость 5 м/с, начинает двигаться с ускорением 2 м/с². Через сколько времени его путь составит 36 м? (задачу решить аналитически и графически) [25].

При изучении понятия мгновенной скорости по механике в 9 классе представляется возможным использовать предел и производную функции.

Эти понятия в курсе математики изучаются в 10 классе [17]. Поэтому учитель физики в 9 классе знакомит учащихся с понятием мгновенной скорости лишь качественно, на основе идеи непрерывности движения. На уроках математики 10 класса при изучении производной функции раскрывают механический смысл производной и записывают формулу скорости υ = х´ или υ(t) = х´(t). При повторении курса физики целесообразно дать более строгое определение мгновенной скорости на основе применения понятия о производной.

Еще одним из основных понятий математики является понятие вектора.

Понятие о векторе и действиях с векторами изучают в курсе геометрии 8 – 9 классов. Поэтому к началу изучения темы «Законы взаимодействия и движения тел» в курсе физики 9 класса школьники уже имеют необходимую математическую подготовку и в этом случае созданы благоприятные условия для реализации межпредметной интеграции. И если учебник по геометрии 8 – 9 класса в некоторой мере учитывает имеющиеся знания по физике (например, п.76), но затем это не используется и не указывается практического применения изучаемого материала [32].

Современное преподавание математики требует органического сочетания экспериментального и теоретического методов изучения физики, выявления сути физических законов на основе доступных понятий элементарной математики. Такой подход одновременно обеспечивает повышение уровня математических знаний, формирует логическое мышление, осознание единства материального мира. Учащиеся начинают испытывать удовлетворение, замечая, что абстрактные математические формулы и уравнения имеют реальное воплощение в физических процессах.

Например, при рассмотрении задач о блоках, наклонных плоскостях и т. д. целесообразно указать учащимся направление поисков решения: записать уравнения второго закона Ньютона для данных тел (грузов), пояснив, что эта система уравнений будет линейной (решение ее известно из курса алгебры). При таком подходе обычно не вызывает затруднения иная формулировка задачи: по известным массам найти силу и ускорения грузов или наоборот.

В курсе физики 9 класса вывод формулы перемещения при равноускоренном движении основывается на формуле площади трапеции, которая учащимся к тому времени неизвестна. Изучение площадей отнесено к концу курса геометрии 9 класса. Учащимся можно предложить получить данную формулу, используя те сведения, которые им уже известны:

– формула площади прямоугольника;

– диагональ прямоугольника делит его на два равных треугольника.

S_OABC = S_OADC + S_ABD = S_OADC + 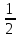S_ADBE

S_x = U_{0x *}t +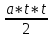




Е В

А D
U_0x U_0x
О С
Осознание учащимися того факта, что они нашли выход из трудного положения, что решили задачу по-своему, заставляет их гордиться собой, своими знаниями, побуждает интерес к изучаемым предметам. Вместе с тем, данный пример позволяет показать, что математика – это факел, освещающий путь всем другим наукам.

Повторение и обобщение знаний о величинах (скорость, время, путь, площадь, объем), формулах, их выражающих, отработку умений их применения можно провести в форме игры-конкурса, целью которого будет подчеркивание взаимосвязи физики и математики; развитие логического мышления; воспитание познавательного интереса к учебным предметам. Вот некоторые вопросы и задачи по физике и математике, которые можно использовать в качестве заданий в ходе игры.

Пример 3

1. 
   В некотором царстве, в некотором государстве была такая единица длины – бумбас. Двор царского дворца имел форму прямоугольника со сторонами 50 и 80 бумбасов. Найдите площадь дворца в квадратных бумбасах. (4000(кв.бумбасов).
   
2. 
   А сам дворец стоял в углу двора, занимал квадрат со стороной 20 бумбасов. Царь решил выложить двор снаружи коврами, имевшими форму прямоугольников со сторонами 2 и 5 бумбасов. Сколько потребуется ковров? (360 ковров.)
   
3. 
   На какую высоту возвышался бы столб, составленный из всех миллиметровых кубиков одного кубометра, выложенных один на другой?
   
4. 
   В бассейне с горизонтальным дном площадью 1 га содержится 10 миллионов литров воды. Можно ли в этом бассейне провести соревнования по плаванию? ( Высота слоя воды 1 дм.)
   
5. 
   Смекалкин спросил младшего брата: «Какой объем имеет 1 лист бумаги?». Брат удивился: «Разве у листа бумаги может быть объем?» Смекалкин дал ему 300 листов бумаги, сложенных в пачку и предложил использовать ее для вычисления объема листа. Длина пачки 300 мм, ширина 203 мм, высота 30 мм. Найдите объем одного листа. (Объем равен 6090 кубических миллиметров.)
   

2.2.3. Математика и информатика

В современных условиях, когда информационные технологии все шире и прочнее входят в нашу жизнь, в практике работы учителей все чаще используется электронно-вычислительная техника. Аспекты применения ЭВТ – это, прежде всего, демонстрационная и вспомогательная. Используя проектор, кинокамеру, фотокамеру, можно организовать демонстрацию различных процессов, происходящих в природе, математике и практике. Для математики – это движение, использование на практике таких утверждений, как « треугольник – жесткая фигура» и др.

Если, в соответствии с учебным планом школы, введено более раннее (в младшем и среднем звене) преподавание информатики, то использовать ЭВМ можно и по другим аспектам. Так, в качестве закрепления, можно предложить учащимся, используя программу Excel построить график квадратичной функции. Это позволит учащимся убедиться в правильности своих рассуждений и математических выкладок.

Точно также учащиеся могут построить графики тригонометрических функций, прежде всего y = sinx, y = cosx, y = tgx, а также более сложных функций. Кроме того, можно привлечь ЭВМ с помощью той же программы Excel для проверки правильности решения тригонометрических и других уравнений и неравенств, нахождения пределов функций. Понятие предела в курсе математики средней школы дается на интуитивном уровне и, поэтому, построение соответствующих графиков функций при стремлении аргумента к тому или иному числу, позволит этот интуитивный уровень свести к интуитивно-наглядному.

В курсе математики средней школы только упоминается о существовании других систем счисления кроме десятичной. В процессе изучения соответствующей темы в курсе информатики значительно расширяется понятие числа, систем счисления, их необходимости, т.к. все электронно-вычислительные машины работают на использовании двоичной системы счисления. Очень интересным получается вечер по математике и информатике, где интегрируются знания учащихся по этим предметам.

Эффектно получаются фокусы, предложенные Я.И. Перельманом в своей книге– «Угадать число спичек», «Не открывая кошельков» и др [24] .

Тема «Алгоритмизация и программирование» изучается на всех ступенях средней школы, но на разном уровне. В начальной школе происходит знакомство на интуитивном уровне с понятиями алгоритма, алгоритмических конструкций, основ алгебры логики. В качестве учебных задач рассматривают бытовые, игровые, сказочные алгоритмы. В средних классах школы в рамках данной темы происходит уточнение понятия алгоритма, основы алгебры логики излагаются на более формальном уровне. И.Н. Фалина в своей работе пишет, что понятие алгоритма является фундаментальным понятием математики и информатики [34]. Первоначально под словом алгоритм понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.

В целях развития познавательного интереса учащихся к данной теме А.А. Чернов в своем учебном пособии предложил задания межпредметного содержания [35]:

Пример 1

- Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе короля. Долго спорили и вот один старый параллелограмм сказал: «Давайте отправимся все в столицу королевства, и кто первым войдет в нее, тот и станет королем!» Рано утром отправились все в путь. Путь им преградила река, которая сказала: «Переплывут меня те, у кого диагонали точкой пересечения делятся пополам!» Часть четырехугольников осталась на берегу, а остальные переплыли. Затем они подошли к высокой горе, которая сказала, что она пропустит только тех, у кого диагонали равны. Пришлось некоторым путникам остаться, а остальные пошли дальше, пока не дошли до узкого моста. Мост пропускал только тех, у кого диагонали пересекаются под прямым углом. Эту преграду прошел один. Кто?

Пример 2

- Составить алгоритм и программу на указанную тему (например, определить тип треугольника; составить программу определения существования треугольника со сторонами (а, b, с)).

Условие существования треугольника известно из геометрии: сумма двух любых сторон должна быть больше третьей. Программа может выглядеть следующим образом [37]:

Programv1;

Vara, b, c: real;

Begin

Writeln ('введите длины трех сторон треугольника');

Readln (a, b, c);

If (a+b>c) and (b+c>a) and (a+c>b)

Thenwriteln ('треугольник существует')

Elsewriteln ('треугольник не существует');

End.

2.2.4. Математика и черчение. Математика и рисование

К началу изучения курса черчения учащиеся знакомы с такими понятиями, как:

- точка, прямая, луч, угол, плоскость, треугольник, четырехугольник и их свойства;

- умеют измерять отрезки и углы;

- знают признаки равенства треугольников;

- имеют представление о перпендикуляре и могут построить серединный перпендикуляр отрезка;

- знают признаки параллельности двух прямых и обратные теоремы;

- знакомы с понятием поперечного масштаба и др.

Вместе с тем, изучение предмета «Черчение» оказывает неоценимую помощь в развитии пространственного воображения школьников. Практика построения аксонометрических проекций плоских и пространственных фигур используется при построении чертежей фигур в стереометрии [2].

Ортогональная проекция широко используется в архитектуре при изображении фасада и плана проектируемых зданий. В техническом черчении при построении комплексных чертежей деталей используется ортогональное проектирование на три взаимно перпендикулярные плоскости. В курсе геометрии в ортогональной проекции строятся изображения тел вращения [2].

Кроме этого метод ортогональных проекций был разработан живописцами Древнего Египта. Ортогональные проекции позволяли древнеегипетскому художнику сообщать зрителю объективную информацию об окружающем мире. При изображении животных, например, выбирался вид сбоку. Очень интересно рисовалась человеческая фигура: голова и ноги изображались сбоку, а грудь и плечи рисовались спереди.

Центральная проекция используется в архитектуре для построения наглядного изображения проектируемых зданий. Этот вид проекций нашел широкое применение в живописи (здесь имеют место, так называемые прямая перспектива, используемая для изображения удаленных от рисующего объектов, и обратная перспектива, лежащая в основе иконописи); кроме этого, на центральном проектировании основан один из важнейших разделов геометрии – проективная геометрия. В живописи наиболее широкое применение находит центральная проекция.

При анализе вышесказанного можно сделать следующий вывод, что возможности применения различных видов проекций, безусловно влияет на развитие кругозора учащихся, на формирование интереса к изучению геометрии.