ПЗ 1 и 2 проектир ИС с ЭТ.doc. Решение задачи линейного программирования в Excel
 Скачать 0.6 Mb.
|
|
Варианты заданий
Контрольные вопросы Зачем нужны сигналы синхронизации? Как связана задача синхронизации и способы кодирования передаваемой информации? Почему в системах передачи данных находят большое распространение коды, использующие метод расщепленной фазы? В каких областях применения можно использовать коды без возврата к нулю? Назовите группы сигналов синхронизации и их назначение. Какие способы используют при осуществлении групповой синхронизации? ЛАБОРАТОРНАЯ РАБОТА № 3 ОПРОС ИСТОЧНИКОВ ИНФОРМАЦИИ Цель работы: получение основных сведений и практических навыков проектирования средств коммутации входных сигналов информационно-измерительных систем. Основные сведения Реальная информационно-измерительная система (ИИС) зачастую имеет большое число информационных входов. Одним из способов передачи информации от каждого источника на приемную часть ИИС является выделение отдельного канала связи под каждый информационный канал, однако стоимость такого метода весьма велика, поэтому на практике он практически не применяется. Более приемлемым способом, обычно и применяющимся на практике, является объединение потоков информации в один канал. Такое решение снижает трудовые и материальные затраты на создание ИИС, но при этом усложняются другие подсистемы ИИС, например, подсистема сбора информации. Одной из основных задач, решаемых этой подсистемой, становится группирование (объединение) потоков информации. Группирование можно проводить как на входе ИИС, используя различного рода аналоговые коммутирующие устройства, так и перед передачей информации в канал связи. Следует учитывать, что второй случай приводит к существенному повышению как сложности ИИС, так и ее стоимости. Этот факт связан с необходимостью параллельной обработки входных информационных потоков, что приведет к существенному повышению требований к вычислительным ресурсам системы и дублированию обрабатывающих трактов ИИС. Поэтому разработчики предпочитают применять коммутацию входных информационных сигналов до начала их обработки. Коммутирующие устройства можно охарактеризовать большим числом параметров, но основными из них можно считать: число каналов Nк; частоту опроса каждого канала Fоп i; информативность коммутатора 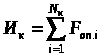 ;погрешность, вносимой в измерения; способ коммутации; способность к адаптации. Наиболее простой способ организации коммутации сигналов с временным разделением канала состоит в использовании ключей (электромеханических, электронных и пр.), объединенных по выходу, причем число опрашиваемых каналов соответствует числу входов коммутатора. Информация из каждого канала поступает на выход коммутатора в течение периода времени, задаваемого генератором тактовых импульсов. Такой способ опроса каналов называется циклическим опросом. Пример простейшего коммутатора, выполненного по схеме с циклическим опросом, приведен на рис. 5. На рисунке приняты следующие обозначения: ГТИ – генератор тактовых и 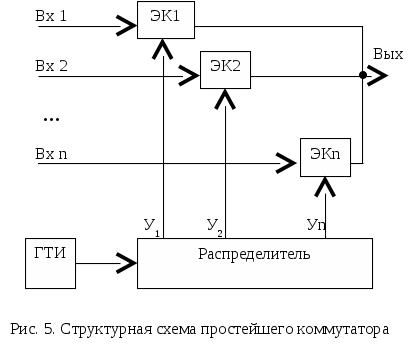 мпульсов, ЭК – электронный ключ, У – сигнал управления.В этом случае каждому сигналу отводится свой интервал времени, в течении которого он передается на вход ИИС. Такой интервал времени называется канальным интервалом. Время опроса всех сигналов, подключенных к коммутатору, называется периодом опроса коммутатора. Необходимо учитывать, что при увеличении числа опрашиваемых каналов и фиксированном периоде опроса, канальный интервал уменьшается пропорционально числу подключаемых каналов. В том случае, если разработчик использует такой метод, частоту опроса следует выбирать по наиболее динамическому источнику, что требуется для минимизации погрешности восстановления. Но в этом случае неизбежно возникает информационная избыточность для других источников. Таким образом, оптимальный коммутатор в самом общем случае должен иметь широкий набор частот опроса источников, причем устанавливать их по каждому каналу отдельно. Такая процедура называется неравномерным опросом каналов. Неравномерный опрос можно реализовать и на базе простейшего коммутатора с циклическим опросом. Так, для повышения частоты опроса конкретного источника используют метод, называемый суперкомпозицией. Суть его заключается в том, что один источник подключается на несколько входов коммутатора. Естественно, что в этом случае число входов коммутатора больше числа источников. Для сохранения равномерности интервала между опросами, что требуется для снижения их коррелированности или для уменьшения погрешности, необходимо соблюдать кратность общего числа входов и числа запараллеленных входов. Например, если число входов составляет 2а, то число запараллеливаемых входов должно составлять ряд геометрической прогрессии: 1, 2, 4, …, 2а-1. В этом случае линейка частот опроса составляет Fоп, 2Fоп, 4Fоп, … 2а-1Fоп. Более сложными методами формирования набора частот опроса каналов являются многоступенчатые системы опроса, которые используются для снижения массы и объемов измерительных цепей. Коммутаторы, на которые поступают сигналы непосредственно с датчиков, называют локальными (ЛК). Обычно локальные коммутаторы имеют равное число входов. Это упрощает работу подсистемы синхронизации и приемной части всей системы. Коммутатор последней ступени обычно называют основным (ОК). Пример многоступенчатого коммутатора показан на рис. 6. Д 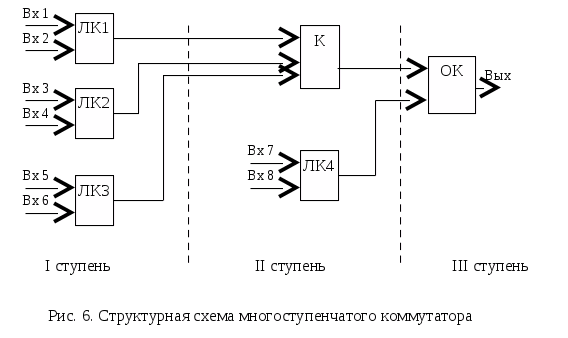 вухступенчатый метод коммутации можно использовать для снижения частоты опроса. Такой метод называют методом субкоммутации. Он необходим, например, в технических системах, где требуется измерять медленно меняющуюся величину или измерять не изменяющиеся в текущем режиме работы величины, по которым происходит контроль системы. Пример структурной схемы 12-канального коммутатора, реализующего субкоммутацию четырех каналов С1 – С4, приведен на рис. 7.Работа такого коммутатора происходит следующим образом. Основной коммутатор ОК производит последовательный циклический опрос каналов S1…S8, причем при каждом опросе канала S3 происходит опрос только одного из каналов С1 – С4. Таким образом, период опроса одного и того же канала Сi будет в четыре раза больше, чем период опроса любого из каналов Si (исключая канал S3). При дальнейшем увеличении числа входов субкоммутатора СК, частота опроса его каналов будет пропорционально снижается. 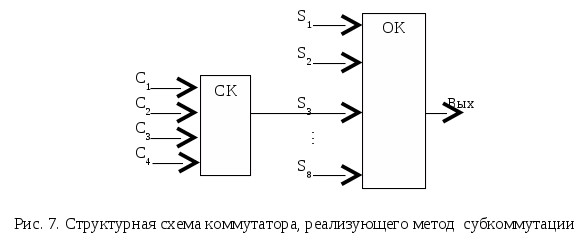 Опрос каналов многоступенчатого коммутатора может производиться двумя способами – последовательным и чередующимся опросами. При первом из них, происходит полный опрос всех каналов коммутаторов более низкого уровня, а затем выполняется переход на следующий канал текущего коммутатора. Чередующийся же опрос характерен тем, что каждый раз при опросе коммутатора нижнего уровня, происходит опрос только одного из его каналов. Примечание: При выполнении лабораторной работы следует использовать блоки библиотек пакета Simulink «Simulink», «DSP blockset» и «Simulink Extras». В качестве коммутирующего элемента следует выбирать элемент «SimulinkSignal RoutingMultiport Switch». Счетчик для управления коммутатором находится в разделе «DSP blockset Signal Management Switches and Counters». На входы коммутатора следует подавать сигналы с генераторов случайных сигналов, заданных в «DSP BlocksetSources». Задание 1) Реализовать коммутатор с простым циклическим опросом. Число каналов коммутатора равно числу входных источников сигнала и определяется по табл. 4. Вывести групповой сигнал АИМ; 2) Согласно варианту задания реализовать систему многоступенчатого опроса источников информации. При реализации трехступенчатых коммутаторов число каналов локальных коммутаторов выбирается равной двум. Вывести групповой сигнал АИМ, рассчитать информативность коммутатора, принимая базовую частоту опроса за единицу. Таблица4 Варианты заданий
Контрольные вопросы В чем состоит необходимость группирования потоков сообщений? Как называется сигнал на выходе коммутирующего устройства? Назовите основные параметры коммутаторов. Почему при реализации метода суперкоммутации выбирают число запараллеленных входов кратным 2n? Какие коммутаторы называют локальными? Назовите основные преимущества использования многоступенчатых коммутаторов? Что такое «канальный интервал»? В каких случаях используется неравномерный опрос источников информации? ЛАБОРАТОРНАЯ РАБОТА № 4 АЛГОРИТМЫ СЖАТИЯ АНАЛОГОВЫХ ДАННЫХ Цель работы: получение основных сведений и практических навыков разработки подсистем однопараметрического сжатия аналоговых данных информационно-измерительных систем. Основные сведения По мере развития систем измерения и передачи информации, объем передаваемых данных как внутри самой системы, так и по каналам связи неуклонно возрастал. Вскоре разработчики столкнулись с физическими ограничениями существующей и даже перспективной аппаратуры связи и связных каналов. Требовалась либо слишком большая полоса частот, либо слишком большое время обработки информации, либо слишком большие объемы запоминающих устройств и т.д. При этом проведенные исследования показали, что далеко не вся передаваемая информация была одинаково ценной, т.е. часть её была избыточной, по некоторым оценкам, в среднем до 70 % от общего объема. Естественным следствием стала разработка средств и алгоритмов сжатия информации, т.е. средств передачи только полезной, безызбыточной информации. Избыточность информации в первую очередь связана с неизбежной коррелированностью выборок при дискретизации, т.е. соседние выборки всегда информационно связаны друг с другом. С другой стороны, регистрируемые параметры зачастую являются нестационарными, что также подразумевает неоднородность данных по информационной ценности. Так, например, в электроэнергетике ряд параметров качества (напряжение, частота) поставляемой электроэнергии в штатных режимах работы энергосистемы имеют стационарный характер. Однако в случае возникновения аварийных ситуаций, по поведению этих параметров можно судить о характере причины, вызвавшей эту аварию. В подобных случаях очень важно иметь данные о поведении критических параметров непосредственно до и во время аварии. Таким образом, при штатном режиме работы не требуется большого объема передаваемой информации, но в аварийном режиме канал связи может быть переполнен важными данными. Следовательно, при разработке ИИС следует учитывать такую информационную неоднородность и применять специальные методы и средства сокращения избыточности информации (сжатия), причем в случае нестационарного сигнала они должны быть адаптивными. Суть методов сжатия данных сводится к анализу поступивших выборок измерительного сигнала и передаче на приемную сторону только тех из них, которые несут максимальное количество информации. Такие выборки называются существенными. Методы сжатия данных могут классифицироваться по различным признакам, однако на настоящий момент наиболее часто используется следующая классификация: Адаптивные и неадаптивные; Необратимые и квазиобратимые. Отличие адаптивных и неадаптивных методов заключается только в их способности приспосабливаться к измерительному сигналу. Первые могут это делать, а вторые разработаны под априорно известные свойства измерительного сигнала. Квазиобратимые методы уменьшают число координат исходного сообщения так, чтобы при восстановлении погрешность не превышала заданного значения. Таким образом, говорить о полном восстановлении сигнала нельзя, всегда есть некоторая погрешность восстановления. В свою очередь, квазиобратимые методы делятся на две группы: а) методы, уменьшающие объем каждой выборки; б) методы, уменьшающие число передаваемых выборок. Объем выборки может быть уменьшен, во-первых, за счет неравномерного адаптивного квантования динамического диапазона выборок, во-вторых, статистическим кодированием значений выборок, в-третьих, нелинейным преобразованием шкалы сообщения. Еще один метод такого класса связан с устранением постоянной (или изменяющейся по известному закону) составляющей исходного измерительного сигнала. Особенность необратимых методов состоит в их способности удалить из измерительного сигнала всю «ненужную» информацию, за счет чего и достигается существенное сокращение объема передаваемой информации. Обычно такие методы используются при отсутствии априорных данных об обрабатываемом параметре. Для некоторых процессов это единственно возможные методы сжатия. Например, случайный процесс с высокочастотным широкополосным спектром возможно сжать только таким методом, т.к. квазиобратимые методы в этом случае не дают выигрыша в объеме сообщения, а иногда и увеличивают его. Следует отметить, что все вышеизложенное относится только к измерительным аналоговым сигналам. Именно аналоговые сигналы невозможно передать без искажения, с нулевой погрешностью восстановления. Для дискретных же сигналов такого ограничения нет. Так, в компьютерной технике широко используются специальные программы-архиваторы, сжимающие цифровую информацию и затем полностью восстанавливающие ее. Эффективность процедур сжатия обычно определяется по отношению к некоторой оптимальной процедуре. На практике это либо равномерно-временная циклическая дискретизация, либо некоторая оптимальная идеальная процедура, которая позволяет получить в каждом отсчете максимум полезной информации). Однако наибольшее распространение на практике получил первый принцип. Самой показательной характеристикой метода сжатия данных является коэффициент сжатия, который можно определить как отношение объемов сообщения до и после сжатия. Однако следует отметить, что для правильного восстановления сообщения, необходимо использовать еще и служебную информацию. Это приводит к тому, что реальный коэффициент сжатия необходимо вычислять по следующей формуле:  ,где I0 – объем исходной информации; Iсж – объем сжатой информации; Iсл – объем служебной информации. Следует отметить, что даже если отношение исходного объема информации и объема сжатых данных будет больше единицы, то реальный коэффициент сжатия может быть как больше, так и меньше единицы. Немаловажным параметром является помехоустойчивость алгоритмов сжатия, которая определяется следующим образом:  , где RП и RСЖ – средние потери до и после сжатия; ,где s и sош – дисперсия ошибки восстановления до и после сжатия, pi ош и pi ош.сж. – вероятности ошибок передачи не сжатого и сжатого сообщения в канале соответственно. До сих пор все рассмотренные параметры были относительными. Абсолютную оценку эффективности алгоритма можно получить в том случае, если использовать понятие энтропии сообщения. Например, коэффициент m показывает насколько алгоритм сжатия приближается к идеальной процедуре сжатия:  ,где Нсж(х) – энтропия после применения метода сжатия, Нmax(х) – максимально возможное количество информации содержащееся в отсчете измеряемого случайного процесса. Качество воспроизведения информации принято оценивать следующим коэффициентом: , где Нош(y) – потери информации за счет ошибок (энтропия ошибки). Важным показателем также является время задержки при восстановлении сообщения. Это время определяется как интервал между моментом поступления очередной выборки на вход блока сжатия и моментом восстановления ее значения на приемной стороне. На практике алгоритмы сжатия данных можно разделить на однопараметрические и двухпараметрические. Различают два типа однопараметрических алгоритмов сжатия: По степени полинома при фиксированном интервале представления; По длине интервала представления при фиксированной степени полинома. Суть работы алгоритмов второго типа состоит в следующем. Все время измерения разбивается на последовательные интервалы, длина которых определяется на основе анализа текущего сообщения при известной погрешности восстановления. Левая граница каждого интервала фиксируется на правой границе предыдущего, а правая граница отодвигается вперед по времени до тех пор, пока погрешность восстановления не превышает заданное значение. В качестве показателя верности обычно используют показатель равномерного приближения, хотя возможно использование показателя среднего квадратического приближения. Действительно, если числовые значения показателей соответствуют одинаковому вероятностному распределению, то на величину коэффициента сжатия выбор показателя погрешности не оказывает влияния, но для расчета показателя равномерного приближения требуется значительно меньше вычислительных операций. Поле допустимого отклонения выборки относительно аппроксимирующего полинома (по оси ординат) обычно называют апертурой, а алгоритмы с контролем максимальной погрешности – апертурными. Величина апертуры составляет удвоенное значение допустимой погрешности. По способу построения восстанавливающего полинома алгоритмы сжатия разделяют на три группы: Экстраполяционные; Интерполяционные; Смешанные (экстраполяция и интерполяция). Экстраполяционные алгоритмы работают следующим образом. По первым (N + 1) выборкам вычисляются коэффициенты полинома Лагранжа степени N. Для каждой последующей выборки вычисляется соответствующее значение при найденных коэффициентах, а разность между фактическим и вычисленным значениями сравнивается с допустимой погрешностью [6]. Рассмотрим работу экстраполяционного однопараметрического алгоритма сжатия первого порядка на передающей стороне. После накопления двух выборок l0 и l1 (по мере поступления, эти выборки передаются в канал связи и поступают на приемную сторону), вычисляется разделенная разность первого порядка по следующей формуле: 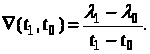 После поступления в момент времени t2 выборки l2, вычисляется значение экстраполирующего полинома в точке t2:  .После этого рассчитывается погрешность восстановления, т.е. разность (модуль разности) выборки  и ее восстановленного значения  . Если полученная погрешность оказывается больше допустимой погрешности д, выборка передается в канал связи, в противном случае – нет. В том случае, когда текущая выборка оказывается существенной и передается в канал связи, интервал экстраполяции обрывается и начинается новый. При этом в качестве первой точки, необходимой для расчета экстраполирующего полинома, выбирается расчетное значение выборки, предшествующей существенной. Второй точкой становится выборка, признанная существенной. Это помогает избавиться от высокочастотных шумов, возникающих при наличии в сигнале резких переходов с одного уровня на другой.На приемной стороне по полученным двум выборкам l0 и l1 строится экстраполирующая прямая , которая продолжается до момента времени поступления очередной существенной выборки lk. В этом случае строится новая экстраполирующая прямая  . Н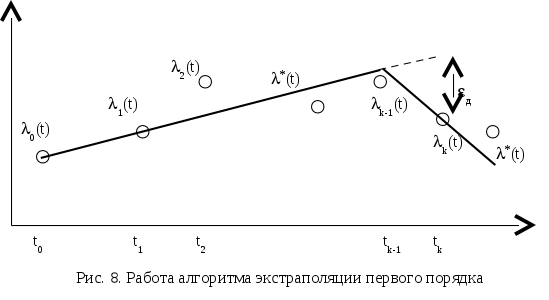а рис. 8 показан пример работы алгоритма.Р  абота интерполяционных алгоритмов происходит в следующем порядке [6]. После накопления (N+2) выборок, по (N+1) выборке, обязательно включая крайние, вычисляются коэффициенты интерполирующего полинома степени N. Затем проверяется погрешность интерполяции этим полиномом оставшихся выборок (тех, которые не использовались при построении полинома).Если хотя бы для одной из выборок не выполняется требование о не превышении текущей погрешности над допустимой, в канал связи передается предыдущая выборка lk-1, которая и считается существенной. Следующий интервал интерполяции начинается именно с нее. На приемной стороне полученные ординаты l0 и lk-1 соединяются прямой  , а следующая прямая проводится через lk-1 и очередную поступившую существенную ординату.В том случае, когда сведения о порядке дифференцируемости измерительного сигнала известны априори, можно заранее определить точки интервала интерполяции, где ожидается максимальная погрешность. Например, модуль погрешности ступенчатой интерполяции достигает максимума в начале и конце интервала аппроксимации, а модуль линейной интерполяции достигает максимума приближенно в середине интервала. Использование описанного метода может значительно сократить объем вычислений, но при этом надо учитывать существование отличной от нуля вероятности появления существенных погрешностей и вне рассчитанного диапазона значений. Для алгоритмов интерполяции существенной операцией является выбор точек, по которым строится аппроксимирующий полином. Математическое решение данной задачи было выполнено Чебышевым и связывало оптимальное расположение точек интерполяции с положением нулей полинома Чебышева. Следует отметить, что основным преимуществом интерполяционных алгоритмов по сравнению с экстраполяционными является более высокий коэффициент сжатия при одинаковой степени аппроксимирующего полинома. Это в первую очередь связано с тем фактом, что соседние выборки, на базе которых строится экстраполирующая кривая, располагаются непосредственно рядом друг с другом. Таким образом, выборки являются сильно коррелированными и, как следствие, предоставляют меньше информации о измерительном сигнале, чем расположенные далеко друга выборки, что характерно для интерполяционных алгоритмов. Приведенные выше рассуждения привели к третьему типу алгоритмов сжатия с однопараметрической адаптацией – к смешанным алгоритмам. Для таких алгоритмов характерно увеличение расстояния между выборками, по которым строится экстраполирующий полином. Используя более сильно разнесенные выборки, такие алгоритмы позволяют увеличивать размер интервала экстраполяции, а, следовательно, и коэффициент сжатия при фиксированной степени полинома. Примечание: При выполнении лабораторной работы следует использовать блоки библиотек пакета Simulink «Simulink», «Simulink Extras» и «DSP blockset». Алгоритм ступенчатой экстраполяции можно реализовать с помощью блока «DSP Blockset Quantizers Quantizer». В этом случае пороговая погрешность задается параметром блока Quantizer Interval. |