ПЗ 1 и 2 проектир ИС с ЭТ.doc. Решение задачи линейного программирования в Excel
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Решение задачи линейного программирования в Excel Для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы. При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь). Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом. Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли. Скачать заметку в формате Word, пример в формате Excel 1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель: Максимизировать: Z = 2500 * х1 + 3500 *х2 При условии, что: 3 * х1 + 10 * х2 ≤ 330 16 * х1 + 4 * х2 ≤ 400 6 * х1 + 6 * х2 ≤ 240 х2 ≥ 12 х1 ≥ 0 2. Создадим экранную форму и введем в нее исходные данные (рис. 1). Рис. 1. Экранная форма для ввода данных задачи линейного программирования Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений. 3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт. Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ» Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).  Рис. 3. Параметры Excel Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).  Рис. 4. Надстройки Excel В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)  Рис. 5. Активация надстройки «Поиск решения» После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2). 4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6) 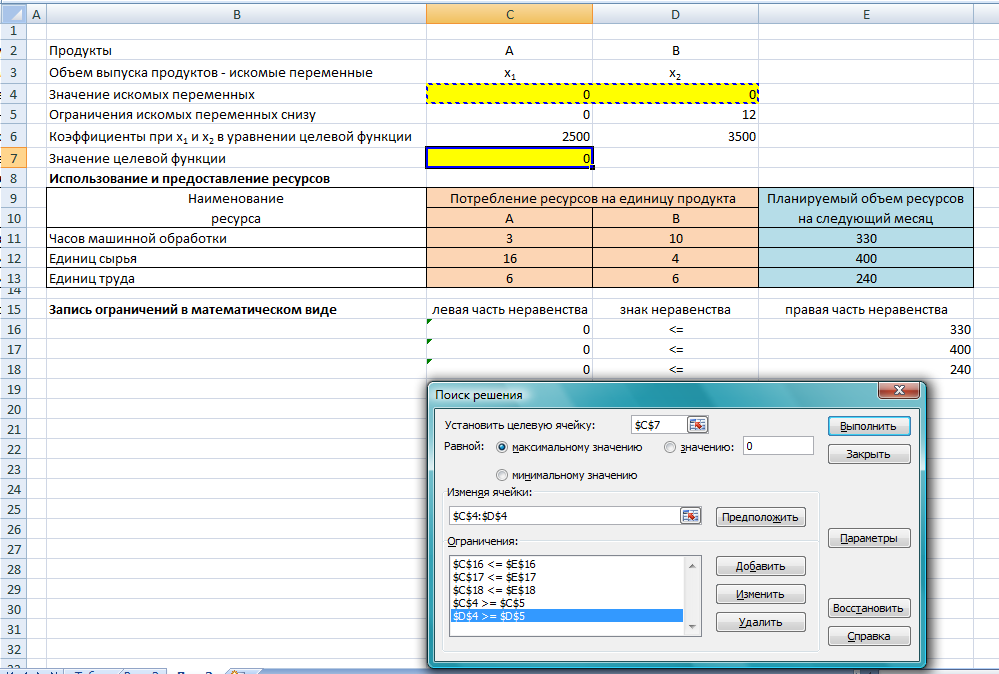 Рис. 6. Заполнение окна «Поиск решения» В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.  Рис. 7. Выбор типов отчета На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В. Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.  Рис. 8. Увеличение погрешности вычислений Теория информационных процессов и систем : методические указания к лабораторным работам № 1–4 для студентов специальности 071900 «Информационные системы и технологии» / сост. А. В. Левенец. – Хабаровск : Изд-во Тихоокеанского гос. ун-та, 2005. – 32 с. Методические указания разработаны на кафедре «Автоматика и системотехника». Лабораторные работы базируются на пакете расширения Simulink системы Mathlab 6.5 и предназначены для ознакомления студентов с принципами и особенностями работы отдельных блоков информационно-измерительных систем. Печатается в соответствии с решениями кафедры «Автоматика и системотехника» и методического совета института информационных технологий. ЛАБОРАТОРНАЯ РАБОТА № 1 МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ Цель работы: получение навыков моделирования случайных сигналов с заданными спектральными параметрами в среде Mathlab 6.5. Основные сведения Модельные преставления сигналов широко применяются в теории управления, теории обработки сигналов и временных рядов, теории передачи информации и во многих других областях. Модели сигналов могут быть как детерминированными, так и стохастическими (случайными). Случайные сигналы отличаются от детерминированных вероятностным характером своих параметров. Иными словами, невозможно точно предсказать какое именно значение приобретет случайный сигнал в каждый конкретный момент времени, но можно предсказать поведение процесса в целом. В задачах анализа и синтеза информационных систем детерминированные сигналы используются редко. Это следует из кибернетического определения информации, поэтому в информационных системах практически все сигналы можно считать реализациями случайных процессов с известными статистическими свойствами. При этом, сигналы можно воспринимать либо как шум (нежелательное влияние внешних искусственных и естественных источников на элементы системы), либо как собственно информацию. Именно поэтому для указанных выше задач необходимым инструментом является генератор случайных сигналов с заданными статистическими свойствами. Применение генератора позволяет в ряде случаев обойтись без натурных экспериментов, которые зачастую связаны с большими финансовыми и трудовыми затратами. Простейшим видом случайного сигнала является случайная величина с равномерным распределением плотности вероятности. Обычно такой сигнал обозначают как Rav[a, b], где a и b верхняя и нижняя границы распределения случайной величины соответственно. Часто на практике используются псевдослучайные генераторы (ПСГ), реализация которых осуществляется достаточно просто. Недостатком таких генераторов является период повторения выходных «случайных» значений. Тем не менее, в зависимости от конкретных задач, можно подобрать генератор такой разрядности, который обеспечит приемлемо большой период повторения. Так, 8-разрядный ПСГ обеспечивает максимальную длину псевдослучайной последовательности равную всего 255, для 16-разрядного генератора она составляет уже 65 535, а для 24-разрядного – 16 777 215 [1]. Цифровая генерация таких последовательностей может осуществляться, например, с помощью регистра сдвига с обратной связью (рис. 1). С помощью элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ – НЕ» на последовательный вход DI регистра сдвига подается сумма по модулю 2 m-го (последнего) и n-го разряда регистра. Можно использовать сумму по модулю 2 и большего числа разрядов регистра. Н 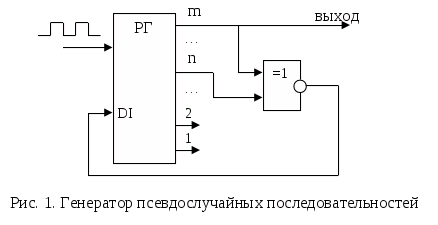 едостатком такой схемы является то, что у нее есть устойчивое состояние, когда в регистре содержатся все единицы. Из такого состояния генератор можно выводить, записывая в него нулевое состояние. Не при всех значениях n и m можно получить последовательность максимальной длины. В табл. 1 приведены оптимальные значения n и m вместе с длиной максимальной последовательности [1]. едостатком такой схемы является то, что у нее есть устойчивое состояние, когда в регистре содержатся все единицы. Из такого состояния генератор можно выводить, записывая в него нулевое состояние. Не при всех значениях n и m можно получить последовательность максимальной длины. В табл. 1 приведены оптимальные значения n и m вместе с длиной максимальной последовательности [1].Таблица 1 Параметры псевдослучайных генераторов
Однако наиболее часто используемыми на практике являются случайные сигналы с нормальным (гауссовским) распределением, что обусловлено именно гауссовским характером большинства естественных и искусственных физических процессов в природе и технике. Такие случайные величины часто представляют как гармонические колебания с фиксированной известной амплитудой А и частотой 0, но случайной фазой φ: Фаза для большинства практически интересных случаев может быть представлена равномерно распределенной случайной величиной Rav[0, 2]. Для получения из равномерно распределенного случайного сигнала гауссовского сигнала с приемлемыми статистическими свойствами обычно используют более сложные формулы. Например, в [2] предлагается следующая формула получения гауссовского случайного сигнала из равномерного: где R(t) – выходной гауссовский сигнал, V(t) – входной сигнал с равномерным распределением. Сигналы, полученные рассмотренными способами, имеют спектр, близкий к «белому». Это означает, что значения спектральных составляющих такого сигнала имеют примерно одинаковое значение для всей оси частот. Однако при исследовании поведения информационных систем часто требуется иметь «окрашенный» сигнал, т.е. сигнал имеющий неравномерный спектр. На рис. 2 приведены примеры белого и окрашенного случайного сигнала, причем сплошной толстой линией показан теоретический спектр. 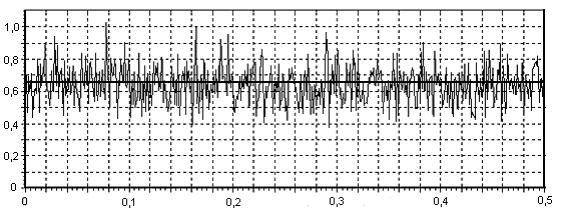 а) «белый» спектр 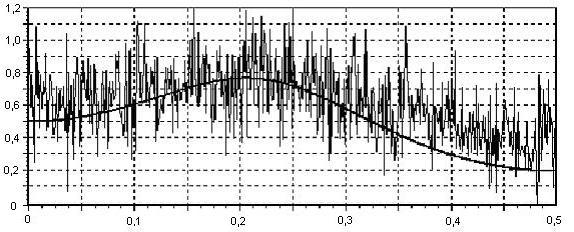 б) «окрашенный» спектр Рис. 2. Примеры спектров реальных моделей случайных сигналов. Существует достаточно много методов моделирования гауссовских процессов. Из них можно выделить: методы, основанные на описании случайной функции n-мерной плотностью вероятности или бесконечной последовательностью обобщенных корреляционных, начальных моментных и характеристических функций; методы, основанные на представлении случайного процесса в виде детерминированной функции случайных величин. Для получения процессов с заданными свойствами применяется метод канонических разложений или описание нелинейными функциями от конечного числа случайных величин; методы, основанные на применении аппарата стохастических дифференциальных уравнений. Такие уравнения находят применение в задачах анализа поведения динамических систем при случайных воздействиях, а также в задачах обнаружения и оценивания параметров случайных сигналов; метод формирующего фильтра, базирующийся на формировании случайного процесса как выхода линейного фильтра, на вход которого подается белый шум. Импульсная характеристика фильтра выбирается в соответствии с требуемой формой спектра формируемого случайного сигнала. На выходе фильтра получается сигнал с требуемой формой спектральной плотности мощности. Случайный процесс, сформированный таким образом, принято называть процессом авторегрессии – скользящего среднего (АРСС-процессом). Наиболее часто используется метод формирующего фильтра, т.к. позволяет получить широкий класс сигналов при манипулировании небольшим числом параметров. Формирование выходного отсчета АРСС-модели случайного процесса происходит по следующей формуле: 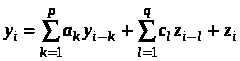 , ,где yi – i-й отсчет выходного процесса; ai – i-й коэффициент авторегрессионного фильтра; ci – i-й коэффициент фильтра скользящего среднего; zi – i-й отсчет входного гауссовского случайного процесса; p и q – порядки фильтров авторегрессии и скользящего среднего соответственно. Таким образом, для формирования текущего значения используются как значения входного белого шума (СС-фильтр), так и сформированные на предыдущих шагах значения выходного процесса (АР-фильтр). Следует отметить, что если СС-фильтр еще можно спроектировать для работы только с предыдущими значениями входного процесса, то АР-фильтру для правильного функционирования обязательно нужно использовать текущий отсчет входного случайного процесса. В зависимости от конкретных задач, измерительный сигнал может быть описан как APCC-, AP- или CC-процесс с конечным числом задающих параметров. Надо отметить, что наиболее часто в технических приложениях используются AP-модели случайных процессов не старше второго порядка [3, 4], т.к. зачастую повышение порядка модели не приводит к существенному повышению точностных параметров модели и слабо влияет на процесс принятия решения при проектировании информационно-измерительных систем (ИИС). Спектральная плотность мощности (СПМ) АРСС-процесса определяется амплитудно-частотной характеристикой формирующего фильтра. Естественно, что на СПМ выходного процесса значительное влияние окажет вид СПМ исходного гауссовского случайного процесса. Для существующих стандартных генераторов характерно случайное, негладкое поведение СПМ, поэтому при проведении исследований прибегают к усреднению либо по входному воздействию, либо по выходной реакции системы. В том случае, когда на вход фильтра подается идеальный гауссовский белый шум, СПМ выходного процесса можно вычислить как [3]: 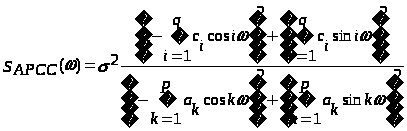 , ,где – круговая относительная частота; 2 – дисперсия АРСС–процесса. Учитывая все вышеизложенное и анализируя приведенную выше формулу, можно определить, что при 2 = 1 для АР- и СС-процессов АЧХ формирующих фильтров описывается следующими выражениями 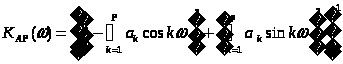 – для АР-фильтра; – для АР-фильтра;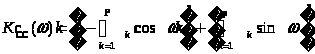 – для СС-фильтра. – для СС-фильтра.Таким образом, используя метод формирующего фильтра, можно получить случайный сигнал с заданными спектральными свойствами при минимальных аппаратно-программных затратах. Однако следует учитывать и тот факт, что неидеальные параметры используемого генератора белого гауссовского шума могут существенно снизить практическую значимость метода формирующего фильтра. Примечание: При выполнении лабораторной работы следует использовать блоки библиотек пакета Simulink «Simulink» и «DSP blockset». Так, например, в качестве элемента задержки следует использовать блок «DSP Blockset Signal operation Integer delay». Вывод гистограмм осуществляется так, как показано на рис. 3. При этом блок «MATHLAB Function» взят из библиотеки «User-Defined Function». В качестве параметра блока следует указать функцию hist(u), а размерность выходной величины установить равной нулю. Блок буфера берется из библиотеки «DSP Blockset Signal management Buffers». Размер буфера выбирается равным размеру выборки, по которой производится построение гистограммы. Наиболее важные блоки, использующиеся при выполнении лабораторных работ, приведены в приложении. 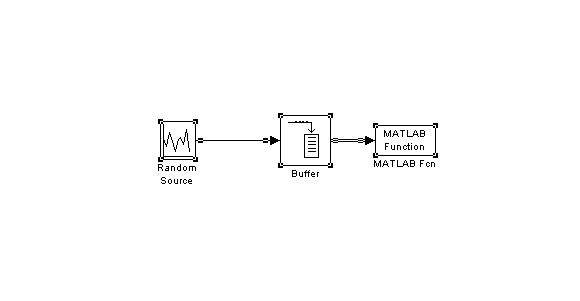 Рис. 3. Вывод гистограммы случайного процесса |
