ПЗ 1 и 2 проектир ИС с ЭТ.doc. Решение задачи линейного программирования в Excel

• Название: Решение задачи линейного программирования в Excel
• Дата: 22.04.2021
• Размер: 0.6 Mb.
• Имя файла: ПЗ 1 и 2 проектир ИС с ЭТ.doc.docx
• Тип: Решение; #197478
• страница: 2 из 4

Задание

1) Исследовать стандартные генераторы случайных чисел с равномерным и нормальным распределением. Вывести графики полученных реализаций случайного сигнала, их СПМ, математическое ожидание и дисперсию, а также гистограммы.

2) Разработать генератор равномерно распределенных псевдослучайных величин, используя параметры табл. 2. Вывести основные статистические параметры полученной последовательности, гистограмму и СПМ. Использовать размер выборки не менее 128.

3) Используя стандартный генератор равномерно распределенных случайных чисел, сформировать генератор белого гауссовского шума. Параметры генератора выбираются из табл. 2 в зависимости от номера варианта. Вывести график полученной реализации случайного сигнала, его СПМ, математическое ожидание и дисперсию, а также гистограмму.

Изменение математического ожидания и дисперсии следует производить по следующей формуле:

,

где r_i – i-й отсчет выходного сигнала;  – требуемое математическое ожидание; R_i – i-й отсчет исходного случайного сигнала с нулевым математическим ожиданием и единичной дисперсией; ² – требуемая дисперсия.

4) Получить случайный процесс, используя метод формирующего фильтра. Тип формирующего фильтра и его коэффициенты выбираются из табл. 2 в зависимости от номера варианта. Для всех вариантов порядок используемых фильтров – 2. Вывести график полученного случайного сигнала, математическое ожидание и дисперсию, реальную и теоретическую СПМ, а также гистограмму полученной реализации.

Таблица 2

Варианты заданий

Вариант	Параметры генератора равномерно распределенных случайных величин			Параметры гауссовского случайного процесса			Параметры АРСС-фильтра случайного процесса
	Разрядность слова	Разрядность регистра	Математическое ожидание		Дисперсия	Тип фильтра		Коэффициенты
1	5	6	0,1		1,5	АР		а1= 0,2; а2= -0,7
2	6	9	0,5		2,2	АР		а1= 0,6; а2= -0,2
3	4	5	0,2		1,1	СС		с1= 0,3; с2= -0,9
4	5	7	0,3		4,5	АР		а1= -0,4; а2= 0,7
5	4	9	0,0		2,7	СС		с1= -0,2; с2= -0,7
6	5	11	0,4		1,8	СС		с1= -0,5; с2= 0,4
7	4	7	0,5		3,6	СС		с1= 0,7; с2= -0,8
8	6	6	0,3		0,6	АР		а1= -0,9; а2= 0,6
9	5	9	0,4		2,9	СС		с1= 0,5; с2= 0,1
10	4	7	0,1		4,7	АР		а1= 0,7; а2= -0,1
11	6	11	0,0		2,5	АР		а1= 0,4; а2= -0,3
12	5	7	0,3		1,6	СС		с1= 0,6; с2= 0,3
13	6	9	0,5		0,7	АР		а1= 0,6; а2= 0,2
14	4	7	0,8		3,0	СС		с1= -0,5; с2= 0,2
15	5	11	0,2		2,2	АР		а1= -0,2; а2= 0,7

Контрольные вопросы

1. Чем объясняется широкое применение моделей случайных сигналов как моделей информационных процессов при проектировании и отладке информационно-измерительных систем?

2. По какому принципу работают генераторы псевдослучайных последовательностей с равномерным распределением?

3. Какими способами можно преобразовать случайную величину с равномерным распределением в «гауссовскую»?

4. Чем отличаются спектры белого равномерного и белого гауссовского случайного процесса?

5. Перечислите методы моделирования гауссовских случайных процессов.

6. Чем отличаются спектры случайных процессов, построенных с помощью АР-фильтров от спектров случайных процессов, построенных с помощью СС-фильтров?

ЛАБОРАТОРНАЯ РАБОТА № 2

ДВОИЧНОЕ КОДИРОВАНИЕ ДАННЫХ

И ТАКТОВАЯ СИНХРОНИЗАЦИЯ

Цель работы: изучение особенностей использования различных типов двоичного кодирования для систем тактовой синхронизации.

Основные сведения

Важной частью любой информационно-измерительной системы является подсистема синхронизации. Основной задачей этой системы – формирование и выделение сигналов синхронизации, что необходимо для правильного приема, обработки и передачи информации. Сигналы синхронизации делятся на две группы: тактовая синхронизация, позволяющая однозначно выделять элементарные единицы сообщения (например, биты), и групповая синхронизация, обеспечивающая уверенный прием групп элементарных элементов (байт, слов и т.п.).

Существуют два способа построения системы синхронизации. В первом случае для передачи сигналов синхронизации используется отдельный канал передачи. К недостаткам такой схемы можно отнести повышенную стоимость и перекрестные помехи между каналами, а к достоинствам – простоту реализации. Во втором случае сигналы синхронизации передаются в одном канале с передаваемой информацией, следовательно, приемный конец канала связи необходимо оборудовать специальными средствами выделения сигналов синхронизации из полезного сигнала. К достоинствам метода можно отнести снижение стоимости канала передачи, к недостаткам – повышение сложности приемо-передающей аппаратуры канала связи. Тем не менее, в настоящее время наиболее часто используется именно второй метод.

Высшим уровнем синхронизации в системах сбора и передачи информации считается групповая синхронизация. Это утверждение подкрепляется тем фактом, что, имея синхронизированную только по тактам последовательность битов, приемник не в состоянии выделить из нее более крупные информационные элементы. Следовательно, говорить об обработке информации не представляется возможным из-за ее фактического отсутствия.

Групповая синхронизация всегда осуществляется при уже установленной тактовой синхронизации. Обычно в информационной посылке содержатся два типа групп элементарных символов: слова, несущие элементарный объем смысловой информации (например, символ или число) и кадры, объединяющие несколько слов в одно информационное целое. Кадры необходимы для передачи некоторого объема связанной информации, например, части пересылаемого текста или файла.

Групповую синхронизацию можно проводить двумя способами: 1) вначале выделяются синхросигналы с частотой следования слов, а затем происходит кадровая синхронизация; 2) вначале обнаруживается кадровый синхросигнал, а затем происходит выделение сигналов пословной синхронизации.

Наиболее простой для решения задачей является выделение сигналов пословной синхронизации при наличии кадровой синхронизации. В этом случае используются простые умножители частоты. Единственным ограничением данного метода является требование одинаковости размера слов в кадре.

Тактовая синхронизация состоит в выделении из группового телеметрического сигнала импульсного напряжения, когерентного частоте следования элементарных символов сообщения. Таким образом, тактовая синхронизация тесно связана со способами кодирования передаваемой информации.

В настоящее время в цифровых системах передачи информации используются различные структуры двоичных кодов. Все эти коды можно условно разделить на три группы [5]:

1. 
   без возвращения к нулю (БВН);
   
2. 
   с возвращением к нулю (ВН);
   
3. 
   коды, использующие метод расщепленной фазы (РФ).
   

Основное различие структур рассматриваемых кодов заключается в использовании тактового интервала, предназначенного для передачи двоичного символа. Первая группа использует весь тактовый интервал для передачи символа. Вторая группа под символ использует только первую половину тактового интервала, а во второй половине всегда передается состояние «0».

Отличие метода расщепленной фазы от первых двух состоит в том, что каждая половина тактового интервала предназначена для передачи своего состояния сигнала. Так, высокий уровень в первой половине тактового интервала говорит о передаче состояния «1», а высокий уровень во второй половине означает состояние «0». Те состояния, когда в обеих обе половинах тактового импульса передаются одинаковые уровни, считаются недопустимыми. На рис. 4 приведены различные структуры двоичных кодов при передаче одного и того же сообщения.

Для различных задач используются различные группы кодов. Так, для передачи цифровой информации в компьютерах используют, в основном, коды без возврата к нулю. Остальные группы кодов, как правило, применяются при передаче сигналов на большие расстояния, когда на первое место выступает необходимость передачи вместе с информацией сигналов тактовой синхронизации.

Сигналы тактовой синхронизации выделяются при помощи системы фазовой автоподстройки (ФАП). Эта система отслеживает тактовую частоту входного сигнала, поэтому очень важным моментом является наличие в спектре входного сигнала ярко выраженной спектральной составляющей. При наличии такой составляющей, задача надежного захвата и слежения за тактовой частотой решается относительно просто.

Н
еобходимо отметить, что рассмотренные коды обеспечивают различные величины вероятности ошибочного приема отдельного бита информации, которая определяется как [6]:

,

где Ф() – функция Лапласа;  – отношение энергии полезного сигнала к спектральной плотности мощности помехи на входе приемника; k_s – коэффициент взаимной корреляции сигналов S₀(t) и S₁(t), являющихся функциями формы сигналов нуля и единицы соответственно.

Коэффициент взаимной корреляции вычисляется следующим образом: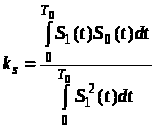

,

где T₀ – период тактового импульса.

Как было указано выше, вид спектра сигнала на входе приемника имеет большое значение для подсистемы синхронизации. Теоретическое спектральное представление для кода БВН можно описать следующим образом [5]:

где  ; Т_с – длительность элементарного символа (бита); а_n принимает значения 0 и 1 с вероятностью 0,5.

Для кода ВН спектральное представление будет иметь аналогичный вид [5]: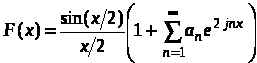

.

Код РФ можно представить как произведение кода БВН и сигнала тактовой частоты. В этом случае спектр кода РФ может быть вычислен как свертка спектров функции БВН и функции сигнала тактовой частоты [5]: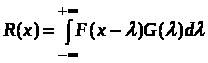

,

где G(x) – спектр функции сигнала тактовой частоты.

Примечание: При выполнении лабораторной работы следует использовать блоки библиотек пакета Simulink «Simulink», и «DSP blockset». Преобразование в последовательный код следует осуществлять с помощью сдвигового регистра, выполненного на триггерах «Simulink Extras  Flip Flops». Необходимо согласовать временной параметр блока «Random Source» (Sample time) и величину времени моделирования для получения требуемой ширины полосы частот спектрограммы (не менее чем в 4–6 раз больше частоты поступления информационных сигналов).

Задание

1) Использовать в качестве источника информации, подлежащей передаче, генератор случайных сигналов «Random Source». Выход генератора преобразовать в цифровой сигнал с разрядностью 8. Каждый отсчет цифрового сигнала следует передавать побитно в заданном кодовом формате. Получить спектр сформированного сигнала не менее чем по 256 выборкам.

2) В качестве исходного сигнала использовать синусоидальный сигнал. Сформировать зашумленный сигнал, для чего добавить к сигналу синусоиды источник, определенный для каждого варианта. Необходимые данные для задания берутся из табл. 3 согласно варианту. Следует учитывать, что в данном случае отношение сигнал/шум (ОСШ) может быть определено как отношение мощностей сигнала и шума (²=А²/², где А – амплитуда синусоиды; ² – дисперсия шума). Закодировать полученный сигнал, аналогично п. 1 задания и получить спектр сформированного сигнала.

3) Используя приведенную выше формулу и табличные данные, рассчитать вероятность ошибочного приема отдельного бита информации для заданного способа кодирования.

Таблица 3