отчет по практике Определение реакций связей составной конструкции и Кинематика плоского механизма с одной степенью свободы. Решение задачи на эвм 7 7 7 7 7 7 7 7 827 7 14. 026 7 809 7 406 7 18. 049 7
 Скачать 349.77 Kb. Скачать 349.77 Kb.
|
СодержаниеВведение 3 Задание С-1 4 `Определение реакций связей составной конструкции 4 рис.1 4 Постановка задачи 4 Составление уравнений равновесия 5 рис.2: Часть составной конструкции – прямоугольная пластина BOAD 5 рис.3: Часть составной конструкции – балка OE 5 Решение задачи на ЭВМ 7 Таблица 2 7 7 7 7 7 7 7 -0.827 7 14.026 7 -9.809 7 -1.406 7 18.049 7 -5.951 7 Максимальное по модулю значение . 7 Контроль решения 7 Задание К-1 9 Кинематика плоского механизма с одной степенью свободы 9 Постановка задачи 9 Составление уравнений 10 Решение задачи на ЭВМ 12 Результаты решения 13 Контроль решения 14 Приложения 18 Приложение 1 18 Приложение 2 21 Список литературы 24 Введение Основной целью учебной практики являлось закрепление полученных знаний по изученным дисциплинам, их применение и ознакомление с особенностями будущей специальности. Для реализации поставленной цели необходимо было решить ряд следующих задач. Задание С1 «Определение реакций связей составной конструкции» (вариант 25) из учебного пособия [1]. Решение задания включает: а) вывод уравнений статики для задачи равновесия составной конструкции; б) сведение к системе линейных алгебраических уравнений, запись матрицы системы и столбца свободных членов; в) написание программы для ЭВМ численного решения системы линейных алгебраических уравнений методом Гаусса; г) получение табличных значений искомых сил реакций для различных исходных параметров задачи; д) контроль решения путем проверки вычисления суммы моментов внешних сил и найденных реакций относительно других точек для элементов механической системы. Задание К1 «Кинематика плоского механизма с одной степенью свободы» (вариант 25) из учебного пособия [1]. Решение задания включает: а) вывод уравнений кинематических связей для плоского механизма; б) сведение к системе обыкновенных дифференциальных уравнений первого порядка, запись начальных условий; в) написание программы для ЭВМ численного решения системы обыкновенных дифференциальных уравнений методом Эйлера I-го порядка; г) построение графиков угловых скоростей и угловых координат элементов механизма; д) контроль решения путем проверки вычисления невязки для геометрических связей, построенных для рассчитываемого механизма. Написание отчета по результатам выполнения заданий с описанием постановки и решения задач и представлением полученных результатов. Для численной реализации решения задач была написана программа для ЭВМ на языке С++ в программной среде Microsoft Visual Studio, оформление отчета выполнено в текстовом процессоре Microsoft Word. Задание С-1 `Определение реакций связей составной конструкции
Постановка задачи Рассматривается плоская механическая конструкция, находящаяся в равновесии под действием заданных сил и наложенных связей (рис.1). Элементы конструкции считаются абсолютно жесткими, стержни, изображенные сплошными линиями, невесомы. Трение в шарнирах и катке 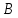 отсутствует. отсутствует. Дано:  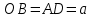 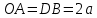 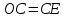 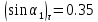 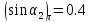 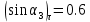 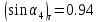 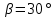 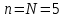 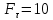 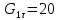 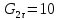 (1) (1)Числовые значения величин задаются формулами: 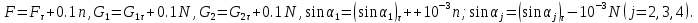 (2) (2)Подставляя в формулы (2) числовые значения (1), получим величины: 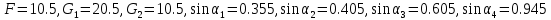 . . Требуется определить реакцию катковой опоры 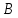 , реакцию в шарнире , реакцию в шарнире 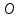 , усилия в невесомых стержнях , усилия в невесомых стержнях 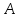 и и 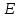 и давление в точке и давление в точке 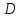 . . Составление уравнений равновесия
На прямоугольную пластину BOAD (рис. 2) действуют силы 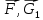 и реакции связей и реакции связей 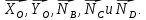 Уравнения равновесия указанных сил: Уравнения равновесия указанных сил: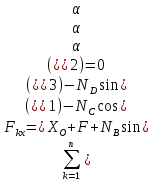 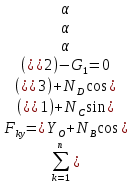 Момент сил для тела относительно точки 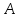 : :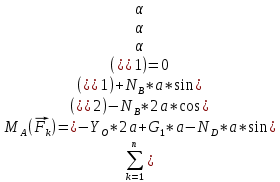 (3) (3)На балку OE (рис.3) действует сила 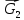 и реакции связей и реакции связей 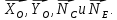 Уравнения равновесия имеют вид: Уравнения равновесия имеют вид:
Подставим в [3] и [4] числовые значения коэффициентов, вычисленных с тремя значащими цифрами после запятой. Тогда:
Решение задачи на ЭВМ Приведем систему уравнений (5) к стандартной матричной форме 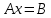 [3]. [3].Матрица СЛАУ 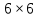 , где , где 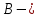 столбец свободный членов столбец свободный членов
При помощи алгоритма Метода Гаусса на языке программирования С++ выполняется решение системы линейных уравнений [8]. Алгоритм реализует прямой и обратный ход. Прямой ход реализует приведение матрицы из Таблицы 1 к ступенчатому виду, а обратный - приведение полученной ступенчатой матрицы к единичной матрице (Приложение 1). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

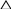








































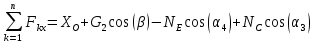 =0
=0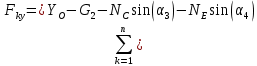 =0
=0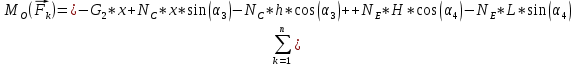 =0
=0