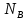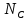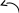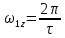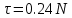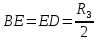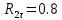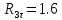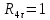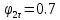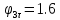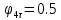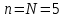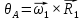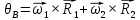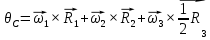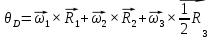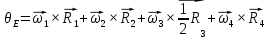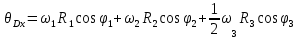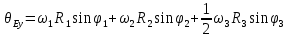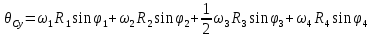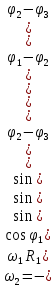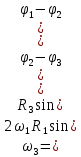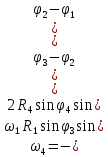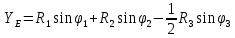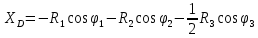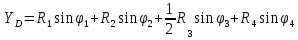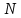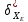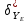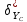отчет по практике Определение реакций связей составной конструкции и Кинематика плоского механизма с одной степенью свободы. Решение задачи на эвм 7 7 7 7 7 7 7 7 827 7 14. 026 7 809 7 406 7 18. 049 7
 Скачать 349.77 Kb. Скачать 349.77 Kb.
|
|
Результаты решения
Максимальное по модулю значение 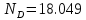 . .Контроль решения Рассмотрим уравнения моментов относительно других точек. Момент сил для балки 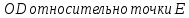 : :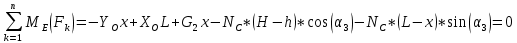 (6) (6) Контроль будет осуществляться подстановкой результатов из Таблицы 2 в уравнение (6): 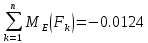 Вычислим невязку: 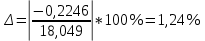 Полученная невязка меньше 3%. Следовательно, можно утверждать, что задача была решена верно. Задание К-1 Кинематика плоского механизма с одной степенью свободы
Постановка задачи Рассматривается механизм с одной степенью свободы и шарнирным соединением звеньев кинематических цепей (рис. 4). В плоском механизме кривошип 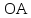 , вращающийся с постоянной угловой скоростью , вращающийся с постоянной угловой скоростью 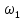 , с помощью шатунов , с помощью шатунов 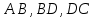 приводит в движение колесо. Колесо катится горизонтально без скольжения. приводит в движение колесо. Колесо катится горизонтально без скольжения. Дано:
Числовые значения задаются формулами: 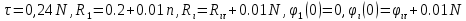 . (8) . (8)Где 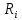 это длина это длина 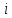 -го звена. -го звена. Требуется: 1. Составить дифференциальные уравнения движения механизма, определяющие во времени угловых скоростей, углов поворота звеньев и скорости точки C. 2. Решить полученную систему уравнений на ЭВМ на интервале времени от 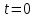 до до 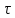 . . 3. Построить графики 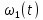 , , 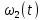 , , 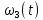 , , 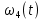 , , 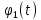 , , 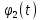 , , 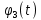 , , 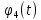 , , 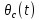 . .Составление уравнений
Составим дифференциальные уравнения для неизвестных угловых скоростей: 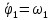 , ,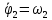 , ,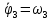 , ,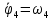 . Они определяются внешними связями, налагаемыми на механизм: в точке . Они определяются внешними связями, налагаемыми на механизм: в точке 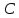 (центр колеса) и в точке (центр колеса) и в точке 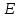 (рис. 5). Тогда уравнения будут выглядеть так: (рис. 5). Тогда уравнения будут выглядеть так: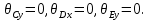 (9) (9) Для вычисления скоростей воспользуемся разложением на геометрическую сумму скорости полюса и скорости точки при вращении фигуры вокруг полюса: 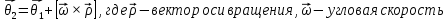 (10) (10) Пользуясь уравнением (10), последовательно находим скорости в соответствии с графом 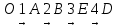 (стрелка обозначает переход от точки-полюса к точке, скорость которой вычисляется; индекс над стрелкой соответствует номеру тела, для которого совершается переход): (стрелка обозначает переход от точки-полюса к точке, скорость которой вычисляется; индекс над стрелкой соответствует номеру тела, для которого совершается переход):
Для проецирования обеих частей уравнения на оси 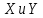 воспользуемся формулой: воспользуемся формулой: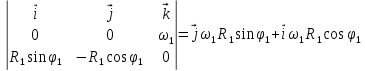 (12) (12)Получим:
Приравнивая нулю левые части уравнений (13), получим систему уравнений для определения 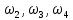 : :
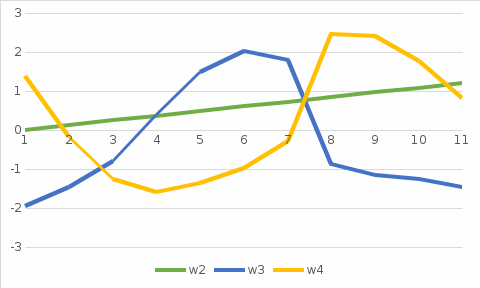
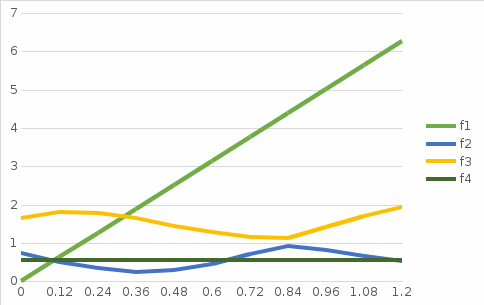
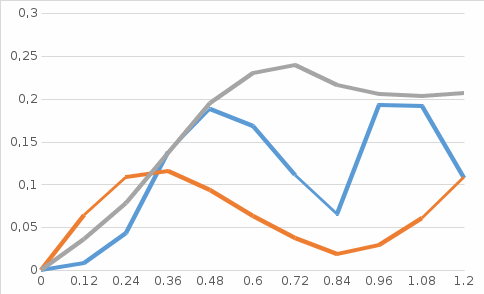
Решение задачи на ЭВМ Вычислим значения углов 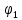 , , 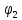 , , 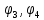 и угловых скоростей и угловых скоростей 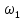 , , 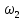 , , 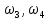 в каждый определённый момент времени – шаг, пока первый стержень не совершит полный оборот. Для этого воспользуемся методом Эйлера первого порядка (Приложение 2). [8] Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. [5] Метод вытекает из определения производной: в каждый определённый момент времени – шаг, пока первый стержень не совершит полный оборот. Для этого воспользуемся методом Эйлера первого порядка (Приложение 2). [8] Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. [5] Метод вытекает из определения производной: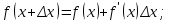 Величина 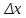 называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения 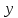 , так как производная , так как производная 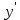 на самом деле не остается постоянной на промежутке на самом деле не остается постоянной на промежутке 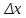 . Исходя из этого выходит ошибка в определении значения функции . Исходя из этого выходит ошибка в определении значения функции 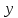 , тем большая, чем больше , тем большая, чем больше 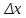 . . 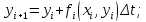 Преобразуя этот метод, получим: 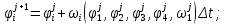 Результаты решения Итоги решения покажем в виде графиков:
Контроль решения Графики на рис.5, рис.6 не имеют разрывов. Значения переменных при 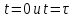 совпадают с хорошей точностью. совпадают с хорошей точностью.Для контроля решения нам понадобятся следующие величины, которые мы находим проектированием векторов на координатные оси:
Контроль решения будем производить по перемещению статичных в вертикальных осях точек 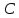 и и 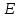 , и в горизонтальной оси точки , и в горизонтальной оси точки 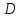 , координаты которых вычисляются по формулам (15). , координаты которых вычисляются по формулам (15). 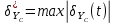 , ,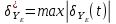 , где , где 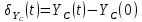 и и 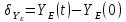 координаты смещения координаты смещения 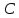 и и 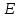 на оси на оси 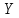 в конкретный момент времени. Погрешности в перемещениях по в конкретный момент времени. Погрешности в перемещениях по 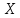 точки точки 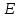 вычисляются по формуле вычисляются по формуле 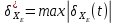 . Здесь . Здесь 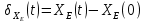 координаты cмещения точки координаты cмещения точки 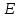 на оси на оси 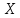
Значение невязок из Таблицы 3 близки к нулю, поэтому можно сделать вывод, что наши вычисления верны. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||