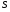Ргр по дисциплине Эконометрика
 Скачать 335.06 Kb. Скачать 335.06 Kb.
|
|
Частные уравнения регрессии: 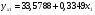 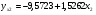 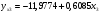 7. Показатель множественной корреляции: 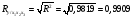 По шкале Чеддока связь оценивается как весьма тесная. Показатели частной корреляции: 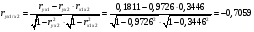   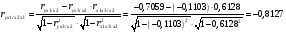 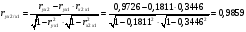  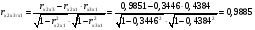 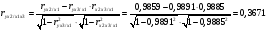 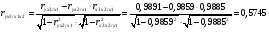 8. Оценим значение коэффициента детерминации до включения переменной 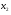 и после включения при помощи функции ЛИНЕЙН ППП MS Excel 2010 и после включения при помощи функции ЛИНЕЙН ППП MS Excel 2010
 После включения по предыдущим расчетам: 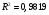 Значение коэффициента детерминации увеличилось после включения переменной, следовательно, включить данную переменную в модель целесообразно. 9. Вычислим средние коэффициенты эластичности: 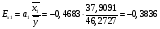 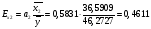 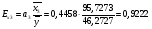 Задание 4. Моделирование одномерных временных рядов. 1. По данным таблицы 3 провести моделирование всех составляющих временного ряда. 2. Рассчитать прогнозные значения на один и два периода вперед.
Решение: Построим график: 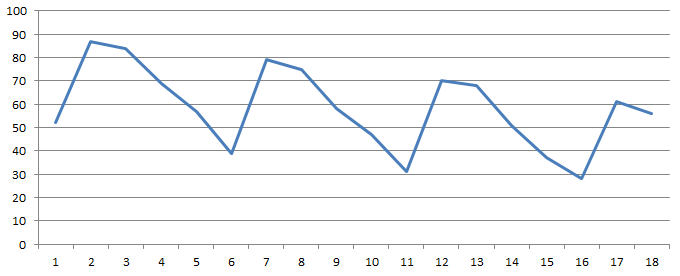 Из графика видны сезонные колебания с периодом 5. Поскольку амплитуда колебаний примерно одинакова, то можно построить аддитивную модель. Проверим величину периода при помощи анализа значений коэффициентов автокорреляции. Расчеты проведем при помощи функции КОРРЕЛ ППП MS Excel 2010
Коэффициент автокорреляции порядка 5 преобладает над остальными коэффициентами, следовательно, в ряду наблюдаются сезонные колебания с периодом 5. Проведем выравнивание ряда динамики при помощи скользящей средней с периодом равным 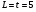 по формуле: по формуле: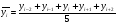 Расчеты проведем в таблице:
Вычислим скорректированные сезонные компоненты:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||