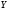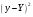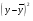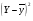Ргр по дисциплине Эконометрика
 Скачать 335.06 Kb. Скачать 335.06 Kb.
|
|
Коэффициенты вычислим из системы уравнений:  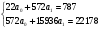 По формулам Крамера получим: 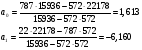 Уравнение линейной регрессии имеет вид: 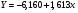 На основании построенного уравнения регрессии можно сделать вывод о прямой зависимости между признаками. 2. Вычислим суммы квадратов отклонений. Расчеты проведем в таблице:
Остаточная сумма квадратов отклонений:  Общая сумма квадратов отклонений: 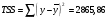 Объясненная сумма квадратов отклонений: 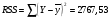 Проверка: 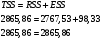 Коэффициент детерминации: 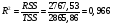 Значение коэффициента близко к 1, что указывает на высокое качество построенного уравнения регрессии. 3. Оценим статистическую значимость уравнения регрессии при помощи критерия Фишера: 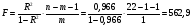 Критическое значение критерия на уровне значимости 0,05 и при 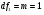 и и 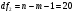 степенях свободы равно: степенях свободы равно: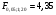 Наблюдаемое значение превышает критическое, следовательно, значение попадает в критическую область, и принимаем альтернативную гипотезу о статистической значимости уравнения регрессии в целом. 4. Вычислим остаточное СКО: 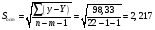 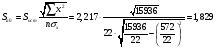 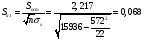 Найдём эмпирические значения 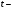 статистики. статистики.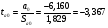 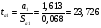 Критическое значение статистики Стьюдента на уровне значимости 0,05 и при 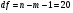 степенях свободы равно: степенях свободы равно: Расчетные значения критерия превышают критическое значение, следовательно, нулевая гипотеза о равенстве нулю отвергается и принимается альтернативная гипотеза о статистической значимости. Таким образом, коэффициенты уравнения статистически значимы. 5. Средний коэффициент эластичности определим по формуле: 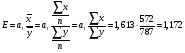 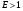 , следовательно, результативный признак эластичен по факторному признаку. , следовательно, результативный признак эластичен по факторному признаку.Задание 2. Построение нелинейной регрессии. 1. Построить уравнение парной регрессии в нелинейной форме (степенная функция), согласно данным таблицы 2, если наблюдаемые значения фактора х в моменты времени t равны 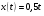 2. Оценить статистическую значимость уравнения. 3. Оценить статистическую значимость параметров регрессии. 4. Рассчитать средние коэффициенты эластичности.
|