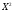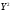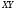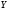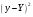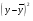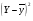|
|
Ргр по дисциплине Эконометрика
Решение:
1. Проведем линеаризацию модели:
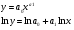
Сделаем замену:
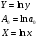
Получим линейную модель:
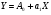
Далее все действия будем производить с преобразованными данными для новой линейной модели, поскольку она повторяет все свойства нелинейной степенной модели по исходным данным.
Составим вспомогательную таблицу с расчетами:
t
|
x
|
y
|
X=lnx
|
Y=lny
|
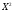
|
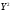
|
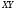
|
1
|
0,5
|
1
|
-0,6931
|
0,0000
|
0,480388
|
0
|
0
|
2
|
1
|
3
|
0,0000
|
1,0986
|
0
|
1,206922
|
0
|
3
|
1,5
|
6,5
|
0,4055
|
1,8718
|
0,16443
|
3,503635
|
0,759015
|
4
|
2
|
11
|
0,6931
|
2,3979
|
0,480388
|
5,749924
|
1,661984
|
5
|
2,5
|
18
|
0,9163
|
2,8904
|
0,839606
|
8,354412
|
2,648474
|
6
|
3
|
28
|
1,0986
|
3,3322
|
1,206922
|
11,10356
|
3,660755
|
7
|
3,5
|
36
|
1,2528
|
3,5835
|
1,569508
|
12,84147
|
4,489409
|
8
|
4
|
47
|
1,3863
|
3,8501
|
1,921828
|
14,82327
|
5,337394
|
9
|
4,5
|
60
|
1,5041
|
4,0943
|
2,262317
|
16,76329
|
6,158237
|
10
|
5
|
74,5
|
1,6094
|
4,3108
|
2,590168
|
18,583
|
6,937802
|
11
|
5,5
|
90,5
|
1,7047
|
4,5053
|
2,906002
|
20,29773
|
7,680185
|
12
|
6
|
106
|
1,7918
|
4,6634
|
3,210547
|
21,7473
|
8,35588
|
Итого:
|
|
|
11,6694
|
36,5985
|
17,6321
|
134,9745
|
47,6891
|
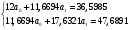
По формулам Крамера получим:
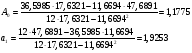
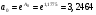
Уравнение степенной модели имеет вид:
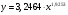
2. Вычислим суммы квадратов отклонений. Расчеты проведем в таблице:
n
|
x
|
y
|
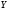
|
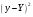
|
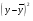
|
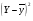
|
1
|
-0,6931
|
0
|
-0,1569
|
0,0246
|
9,3016
|
10,2833
|
2
|
0
|
1,0986
|
1,1775
|
0,0062
|
3,8074
|
3,5055
|
3
|
0,4055
|
1,8718
|
1,9583
|
0,0075
|
1,3878
|
1,1916
|
4
|
0,6931
|
2,3979
|
2,5120
|
0,0130
|
0,4250
|
0,2893
|
5
|
0,9163
|
2,8904
|
2,9417
|
0,0026
|
0,0254
|
0,0117
|
6
|
1,0986
|
3,3322
|
3,2927
|
0,0016
|
0,0797
|
0,0590
|
7
|
1,2528
|
3,5835
|
3,5896
|
0,0000
|
0,2848
|
0,2913
|
8
|
1,3863
|
3,8501
|
3,8466
|
0,0000
|
0,6404
|
0,6349
|
9
|
1,5041
|
4,0943
|
4,0734
|
0,0004
|
1,0909
|
1,0477
|
10
|
1,6094
|
4,3108
|
4,2762
|
0,0012
|
1,5900
|
1,5039
|
11
|
1,7047
|
4,5053
|
4,4597
|
0,0021
|
2,1183
|
1,9876
|
12
|
1,7918
|
4,6634
|
4,6274
|
0,0013
|
2,6035
|
2,4885
|
Итого:
|
11,6695
|
36,5983
|
36,5983
|
0,0606
|
23,3549
|
23,2943
|
Оценим статистическую значимость уравнения регрессии при помощи критерия Фишера:
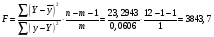
Критическое значение критерия на уровне значимости 0,05 и при 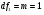 и и 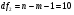 степенях свободы равно: степенях свободы равно:
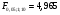
Наблюдаемое значение превышает критическое, следовательно, значение попадает в критическую область, и принимаем альтернативную гипотезу о статистической значимости уравнения регрессии в целом.
3. Вычислим остаточное СКО:
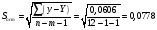
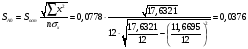
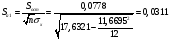
Найдём эмпирические значения 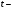 статистики. статистики.
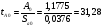
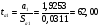
Критическое значение статистики Стьюдента на уровне значимости 0,05 и при 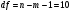 степенях свободы равно: степенях свободы равно:
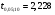
Расчетные значения критерия превышают критическое значение, следовательно, нулевая гипотеза о равенстве нулю коэффициентов регрессии отвергается и принимается альтернативная гипотеза о статистической значимости. Таким образом, коэффициенты уравнения статистически значимы.
5. Средний коэффициент эластичности для степенной модели определим по формуле:
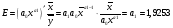
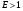 , следовательно, результативный признак эластичен по факторному признаку. , следовательно, результативный признак эластичен по факторному признаку.
Задание 3. Построение многофакторных уравнений регрессии.
Провести оценку мультиколлинеарности факторов.
Построить уравнение множественной регрессии в линейной форме, считая, что значения фактора y расположены под номером n, а значения факторов x1, x2, x3 - под номерами n1, n2, n3 соответственно в таблице 1.
Оценить статистическую значимость уравнения.
Оценить значимость коэффициентов чистой регрессии.
Построить уравнение регрессии в стандартизованном масштабе.
Построить частные уравнения регрессии.
Определить показатели множественной и частной корреляции.
Оценить целесообразность включения переменной x2 в модель после включения переменных x1 и x3.
Рассчитать средние частные коэффициенты эластичности.
y
|
x1
|
x2
|
x3
|
25
|
45
|
25
|
72
|
27
|
43
|
27
|
74
|
30
|
40
|
26
|
76
|
31
|
36
|
29
|
75
|
35
|
38
|
32
|
79
|
41
|
34
|
32
|
78
|
42
|
31
|
30
|
82
|
45
|
28
|
33
|
85
|
47
|
25
|
35
|
89
|
40
|
44
|
32
|
89
|
49
|
36
|
37
|
94
|
45
|
32
|
36
|
92
|
46
|
29
|
35
|
91
|
49
|
37
|
38
|
99
|
50
|
33
|
38
|
98
|
54
|
43
|
42
|
111
|
56
|
39
|
42
|
109
|
57
|
42
|
44
|
114
|
61
|
42
|
47
|
121
|
61
|
46
|
47
|
124
|
63
|
44
|
49
|
126
|
64
|
47
|
49
|
128
|
Решение:
1. Для оценки мультиколлинеарности факторов построим матрицу коэффициентов парной корреляции при помощи инструмента «корреляция» MS Excel 2010.
|
y
|
x1
|
x2
|
x3
|
y
|
1
|
|
|
|
x1
|
0,181098
|
1
|
|
|
x2
|
0,972627
|
0,344578
|
1
|
|
x3
|
0,953721
|
0,438408
|
0,985148
|
1
| |
|
|
 Скачать 335.06 Kb.
Скачать 335.06 Kb.
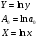
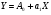
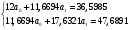
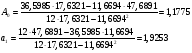
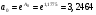
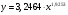
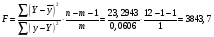
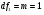 и
и 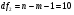 степенях свободы равно:
степенях свободы равно: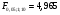
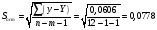
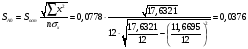
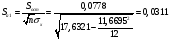
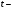 статистики.
статистики.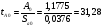
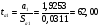
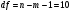 степенях свободы равно:
степенях свободы равно: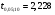
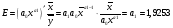
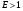 , следовательно, результативный признак эластичен по факторному признаку.
, следовательно, результативный признак эластичен по факторному признаку.