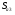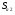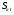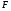Ргр по дисциплине Эконометрика
 Скачать 335.06 Kb. Скачать 335.06 Kb.
|
 Решим данную систему матричным способом при помощи функций МОБР и МУМНОЖ ППП MS Excel 2010  Уравнение имеет вид: 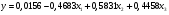 3. Вычислим теоретические значения и вычислим квадраты отклонений:
Оценим статистическую значимость уравнения регрессии при помощи критерия Фишера: 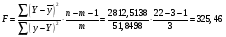 Критическое значение критерия на уровне значимости 0,05 и при 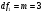 и и 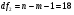 степенях свободы равно: степенях свободы равно: Наблюдаемое значение превышает критическое, следовательно, значение попадает в критическую область, и принимаем альтернативную гипотезу о статистической значимости уравнения регрессии в целом. 4. Ввиду сложности расчета воспользуемся функцией ЛИНЕЙН ППП MS Excel 2010
Значения соответствуют показателям:
Найдём эмпирические значения 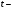 статистики для коэффициентов. статистики для коэффициентов.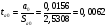 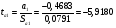 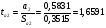 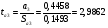 Критическое значение статистики Стьюдента на уровне значимости 0,05 и при 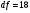 степенях свободы равно: степенях свободы равно: Расчетные значения критерия для коэффициентов 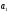 и и 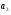 попадают в критическую область, следовательно, нулевая гипотеза о равенстве нулю коэффициентов регрессии отвергается и принимается альтернативная гипотеза о статистической значимости. попадают в критическую область, следовательно, нулевая гипотеза о равенстве нулю коэффициентов регрессии отвергается и принимается альтернативная гипотеза о статистической значимости. Расчетные значения критерия для коэффициентов 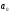 и и 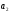 попадают в область принятия нулевой гипотезы, следовательно, данные коэффициенты статистически не значимы, случайно отличны от нуля и можно принять их равными нулю. попадают в область принятия нулевой гипотезы, следовательно, данные коэффициенты статистически не значимы, случайно отличны от нуля и можно принять их равными нулю.Уравнение регрессии примет вид:  5. Уравнение в стандартизированном масштабе имеет вид:  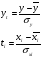 Коэффициенты связаны между собой соотношениями: 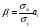 Получим:  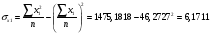 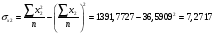 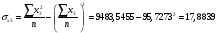 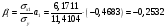 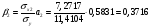 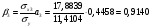 Получим уравнение: 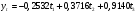 6. Построим частные уравнения регрессии при помощи функции ЛИНЕЙН ППП MS Excel 2010
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||