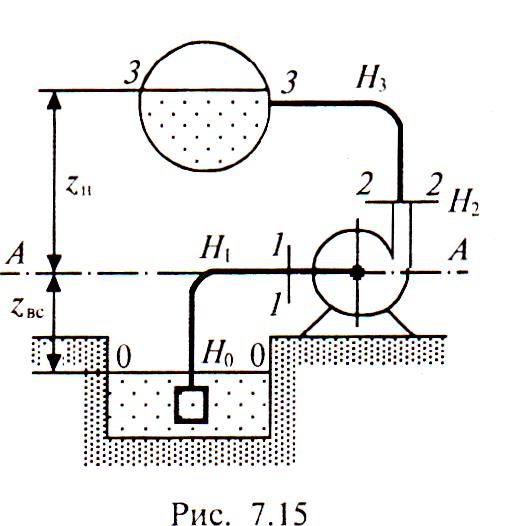
Нижняя заправка. Теория. Рис. Расчетная схема нижней заправки самолета топливом

• Название: Рис. Расчетная схема нижней заправки самолета топливом
• Анкор: Нижняя заправка
• Дата: 26.01.2023
• Размер: 0.88 Mb.
• Имя файла: Теория.docx
• Тип: Документы; #906318
• страница: 3 из 4

,

где п=S₁/S₂—степень сужения конфузора.

Небольшие вихреобразования и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Для ликвидации этих вихреобра-

Рис.1.12.

зований и связанных с ними потерь рекомендуется коническую часть плавно сопрягать с цилиндрической или коническую часть заменять криволинейной, плавно переходящей в цилиндрическую (рис.1.12). При этом можно иметь весьма значительную степень сужения при небольшой длине вдоль

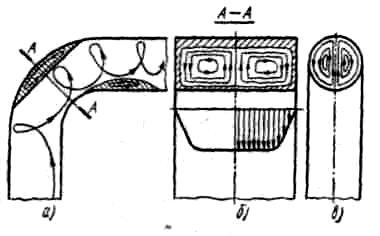
оси и при весьма небольших потерях. Коэффициент сопротивления такого плавного сужения, называемого соплом, меняется примерно в пределах ζ = 0,03 - 0,10, в зависимости от степени сужения, плавности и числа Re (большим числам Re соответствуют малые значения ζ и наоборот),

Повороты потока

Плавный поворот трубы называется отводом. Схема течения представлена на рис.1.13. Появление радиального градиента давления в по-

Рис.1.13. Структура потока в отводе а - продольный разрез; б - поперечное сечениепрямоугольного канала; в - поперечное сечение канала круглого сечения

Рис.1.14. Изменение профилей скоростей и давлений в колене и в трубе за ним

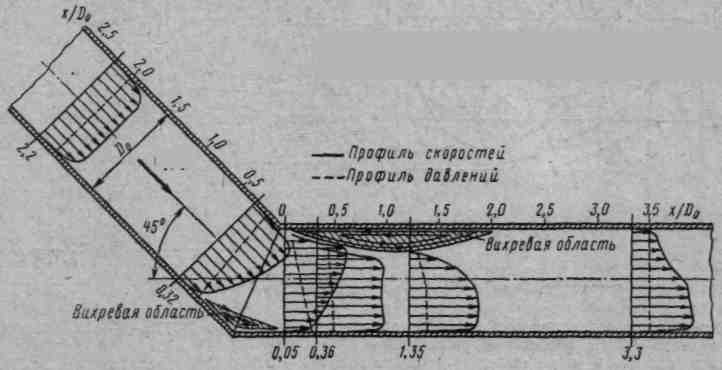
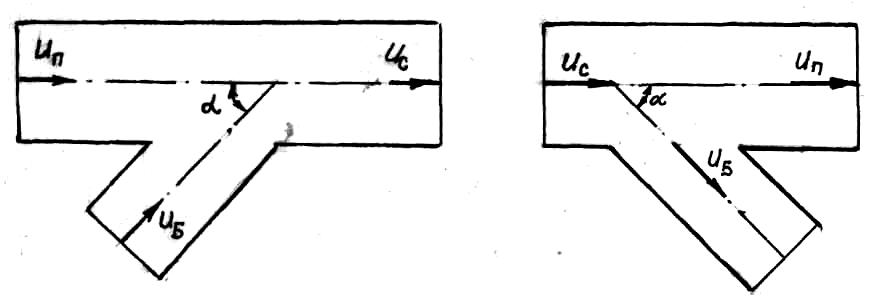
вороте приводит к возникновению так называемого парного вихря (см. поперечные сечения каналов), который, налагаясь на основной поток, придает линиям тока винтообразный характер. Кроме парного вихря, радиальный градиент давления в повороте служит причиной появления возвратных течений, как на внешней стороне поворота, так и на внутренней. Потери вызваны трением и вихреобразованием, в которой коэффициент потерь зависит от относительного радиуса R/d(R -средний радиус поворота, d - диаметр трубы) угла поворота δ и формы поперечного сечения канала и рассчитываются по формуле, предложенной Г.Н.Абрамовичем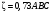

,

где коэффициентыА, В и С учитывают влияние угла изогнутости отвода, относительного радиуса закругления отвода и относительной вытянутости поперечного сечения отвода Значения этих коэффициентов находятся в справочниках, например, в /5/.

Внезапный поворот трубы, или колено, вызывает значительные потери энергии, так как в нем происходят отрыв потока с вихреобразованиями (рис.1.14). Потери энергии тем больше, чем больше угол δ. Коэффициент потерь колена круглого сечения при δ = 90˚ достигает значения 1,0. Поэтому применение колен не рекомендуется.

Потери при слиянии и разделении потоков.

Слияние и разделение потоков происходит в тройниках (рис.1.15). Тройники разделяются на вытяжные и приточные. В вытяжном тройнике происходит слияние потоков (рис.1.15,а), а в приточном - разделение потоков (рис.1.15,б). Геометрически тройники характеризуются углом ответвления α

а) б) Рис.1.15

и отношениями площадей сечений обоих ответвлений SБ/SC, SП/SСиSБ/SП. В каждом тройнике могут изменяться отношения расходов QБ/QCиQП/QС. В гидросистеме с тройниками необходимо учитывать

потери энергии и на боковое ответвление и на проход, в зависимости от рассматриваемой ветви системы, при этом необходимо понимать, что в месте слияния или разветвления потоков давления одинаковы как в транзитном потоке, так и боковом. Для характеристики потерь в тройниках пользуются обычно коэффициентами местных потерь на боковое ответвление ζ_БС и коэффициентом местных потерь на проход ζ_ПС, вычисляемых в приведенном случае по скорости в сборном рукаве u_C. В вытяжном тройнике потери энергии обусловлены смешением потоков и потерями на поворот, иногда вызывающим местный отрыв потока. При вычислении потерь в тройниках необходимо представлять, что в точке слияния (разветвления) потоков (С) давление одинаково и для линий тока на проход (П), и для бокового ответвления (Б)

В приточном тройнике при разделении потоков потери обусловлены потерями на поворот в боковое ответвление, а при проходе – потерями на внезапное расширение в месте разветвления потока. Последние резко растут при увеличении площади отвода, где потери вычисляются по скорости жидкости в сечении сборного рукава тройника.

2. Назначение, состав и принцип действия гидравлических систем

Гидравлические системы широко применяются в технике для транспортировки жидкости от места ее хранения к потребителю. Это может быть транспортировка нефти (нефтепроводы), системы топливопитания, смазки, водоснабжения или отопления завода или жилого дома, организация истечения жидкости из насадков (камеры сгорания, системы смазки, пожарные системы, фонтаны) и т.д.

Гидравлическая система представляет собой набор гидравлических элементов, которые соединены в определенном порядке, обусловленном назначением и пространственным расположением системы. Гидравлическими элементами являются трубопроводы, баки, насосы, всевозможные виды местных сопротивлений. Обычно система имеет гидравлические элементы, предназначенные для хранения жидкости (баки), передачи жидкости на расстояние (трубопроводы), очистки жидкости (фильтры), управления потоком жидкости (краны, вентили, клапаны, заслонки, термостаты), измерений (расходомеры различных типов), изменения направления или разделения потока жидкости (колена, отводы, тройники, коллекторы), изменения скорости потока жидкости (сужения, расширения), поддержания постоянного уровня жидкости (поплавковые камеры), дозирования и организации истечения жидкости (жиклеры, форсунки, распылители).

Гидравлические системы бывают разомкнутыми или замкнутыми (циркуляционными). Система может иметь насос или не иметь его (разомкнутая самотечная система, замкнутая термосифонная система). Магистраль, по которой жидкость поступает к насосу, называется всасывающей, а магистраль, по которой жидкость движется от насоса, - нагнетающей или напорной.
3. Методические указания к расчету гидравлических систем

3.1. Методика расчета гидравлической системы

Расчет гидросистемы включает в себя следующие этапы.

1. В общем случае система разбивается на участки.

2. Выбирается расчетный участок.

3. Части системы, окружающие расчетный участок, отбрасываются и заменяются условиями, определяющими движение жидкости на границах участка.

4. Записываются основные и вспомогательные уравнения, необходимые для описания движения жидкости в выделенном участке.

5. Формулируются граничные условия.

6. Записанные уравнения решаются совместно с граничными условиями и тем самым определяются значения искомых величин.

При использовании уравнения Бернулли рекомендуется сначала записать его в общем виде, а затем переписать с заменой его членов численными значениями (граничными условиями) и исключением слагаемых, равных нулю.

Необходимо помнить:

- плоскость сравнения 0 - 0 удобно располагать так, чтобы ордината z сечений системы отсчитывалась от нее вверх;

- потери полного давления всегда записываются в правой части уравнения, так как уравнение Бернулли записывается по потоку (сечение 2-2 всегда находится после сечения 1-1 в направлении течения);

- величина потерь полного давления на расчетном участке в общем случае складывается из путевых потерь и потерь в местных сопротивлениях;

- при расчете потерь в местных сопротивлениях по формуле (1.4) следует учитывать, при какой скорости определены коэффициенты сопротивления.

Проводя разбиение системы на ряд расчетных участков, необходимо руководствоваться определенными требованиями при выборе граничных сечений участков. Эти требования определяются структурой гидравлической системы и условиями ее работы. При правильном выборе расчетных участков число уравнений будет равно числу неизвестных.

Принцип наложения потерь применяется не только в отношении отдельного элемента системы или канала, но и при гидравлическом расчете всей гидравлической сети в целом. Он означает, что определенные для отдельных элементов сети потери арифметически складываются и эта сумма определяет общее сопротивление гидросистемы или ее участка.

При расчете гидравлической системы в инженерной практике принято представлять ее в виде трубопровода составленного из путевых и местных потерь. Целесообразность такого представления диктуется главной задачей расчета – определения потерь энергии (давления) на расчетном участке. Решение такой задачи необходимо для подбора насоса, обеспечивающего необходимые характеристики гидросистемы.

В зависимости от конфигурации различают простые и сложные трубопроводы.

Простым называюттрубопровод, не имеющий разветвлений от места забора до места потребления.

Разветвленные трубопроводы – сложные. Они бывают такие:

1. 
   разветвленные;
   

б) трубопроводы с параллельным соединением;

в) кольцевые.

Предлагаемой частной задачей расчета является определение перепада давлений 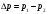по заданному массовому (G)или объемному (Q)расходу и размерам простого трубопровода.

3.2. Простой трубопровод

Итак, простым трубопроводом называется трубопровод постоянного сечения, без разветвлений, содержащий в общем случае несколько местных сопротивлений (рис.3.1).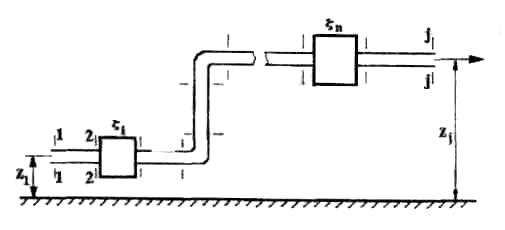



Рис.3.1

Уравнение Бернулли для участка 1 - j может быть записано в таком виде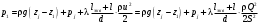

(3.1)

или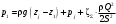

, (3.1а)

где 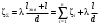– суммарный коэффициент сопротивления трубопровода, а l– суммарная длина простого трубопровода. При использовании в расчете массового расхода G формула (3.1а) примет такой вид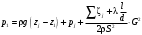

_{. (3.1б)}

Если величину р₁ - необходимо определить, то ее называют потребным давлением и обозначают p_потр. Если эта величина задана, то ее называют располагаемым давлением и обозначают p_расп. Из формулы для потребного (располагаемого) давления видно: потребное давление должно затратиться на преодоление гидравлических сопротивлений 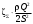при подъеме жидкости с высоты z₁ до высоты z_j с объемным расходом Q и на обеспечение необходимого давления p_jна этой высоте. Не следует упускать из виду, что формулы (3.1) записаны для случая равенства скоростей на входе и выходе рассматриваемого участка трубопровода постоянного сечения.

3.3. Трубопровод с насосной подачей

В гидравлическую сеть очень часто включаются насосы. В практике используются как системы с незамкнутым трубопроводом, так и системы с замкнутым трубопроводом. Первая часто используются в системах топливоподачи, смазки, охлаждения и т.д., вторая – в замкнутых тепловых сетях, системах охлаждения двигателей внутреннего сгорания.

Рассмотрим сначала незамкнутый трубопровод с насосной подачей жидкости. На рисунке 3.2 приведена схема гидравлической сети; часть трубопровода до насоса называется всасывающей, а после насоса - нагнетающей или напорной. Рассмотрим всасывающую часть трубопровода (сечения 0-0 и 1-1). Для нее уравнение Бернулли в напорной форме имеет вид: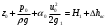

, (3.2)

Отсюда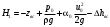

. (3.2а)

Рис.3.2. Разомкнутая система с насосной подачей жидкости

где z0 =–zвс, так как за плоскость сравнения принята плоскость А –А; Δh1–потери напора на участке всасывания, H1 –полный напор на входе в насос (сечение 1-1). Поскольку жидкость в участок всасывания подается из резервуара большого поперечного сечения, то скорость жидкости на свободной поверхности 0-0 можно принять равной нулю; кроме того, координата z1 сечения входа в насос 1-1 также равна

нулю. Исходя из этого, получим уравнение (3.2б), показывающее, что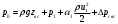

(3.2б)

давление р₀>p₁ и оно затрачивается (с помощью насоса) на подъем жидкости на высоту z_вс, сообщение ему кинетической энергии α₁ρu₁²/2, преодоление всех сопротивлений и сохраняется в виде давления p₁>р_нп где p_нп - давление насыщенных паров жидкости. При p₁<p_нп перед насосом возникает кавитация. Условием нормальной работы этой системы является отсутствие кавитации в насосе. Кавитация возникает тогда, когда давление в жидкости равно или ниже давления насыщенных паров этой жидкости. Жидкость закипает, поток становится двухфазным, состоящим из смеси жидкости и пара. Это приводит к непроизводительной работе насоса и возможному выходу его из строя. Кавитация в гидравлической системе явление вредное. Для ее исключения давление на входе в насос должно быть выше давления насыщенных паров на некоторую величину р_нп, называемую антикавитационным запасом. Следовательно, в системе имеется сечение, в котором известно давление. Может быть, известно давление p₀ на свободную поверхность жидкости - поверхность раздела жидкости и газа. Если размеры свободной поверхности намного больше площади проходного сечения трубопровода, по которому протекает жидкость, то с большой степенью точности можно полагать скорость жидкости на свободной поверхности равной нулю.

Таким образом, граничные сечения, выделяющие расчетный участок системы, рекомендуется располагать:

- в тех сечениях системы, где давление известно или его необходимо определить;

- в тех сечениях системы, где скорость жидкости известна или ее необходимо определить.

Возникновение кавитации сильно зависит от давления р₀, которое зависит от положения резервуара, р₀ = р₀(Н), где Н - высота на которой находится резервуар. В авиационных двигателях с ростом высоты полета Н для предотвращения кавитации можно увеличить давление p₁, уменьшая величину z_вс и сопротивление участка всасывания Δp_r1. Повысить давление р₀ можно путем наддува бака с топливом. Наддув ограничен прочностью бака, поэтому часто под баком устанавливают подкачивающий насос, подающий топливо к основному насосу под необходимым давлением p₁ = p_нп + Δр_нп, где Δр_нп - запас по кавитации (антикавитационный запас).

Для расчета всасывающего трубопровода используют уравнение (3.2). Из него можно найти, например, потребное давление в резервуаре р₀ при заданных параметрах z₁ , p₁, G и Δp_вс.

Полный напор, которым обладает жидкость на входе в насос, определим из (3.2):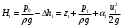



Рассмотрим теперь нагнетающую часть трубопровода. Запишем уравнение Бернулли для участка системы, ограниченного сечениями 2-2 и 3-3 (рис. 3.2) с целью определения полного напора на выходе насоса: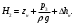

(3.3)

Здесь Δh_н – потери напора на участке нагнетания

Скорость жидкости на свободной поверхности, на которой расположено сечение 3-3 u₃=0 (размер бака много больше поперечногосечения трубопровода подачи.

Полезный напор насоса равен разности полныхнапоров на выходе и входе в насос: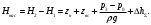

(3.3а)

Здесь

Δh_∑=Δh_вс+Δh_н.

Напор насоса затрачивается на подъем жидкости на высоту (z_вс+z_н), повышение давления (р₃–р₀) и на преодоление гидравлических потерь как в магистрали всасывания, так в магистрали нагнетания.

Обозначим: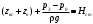

и назовем эту величину статическим напором гидросистемы;

Тогда уравнение (3.3а) может быть записано в таком виде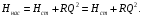

(3.3б)

Сумму в правой части уравнения 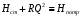назовем потребным напором для разомкнутой сети с насосной подачей. В принятых обозначениях уравнение (3.3а) может быть записано в качестве равенства

Н_нас=Н_потр,

позволяющее сказать, что на установившемся режиме работы разомкнутой гидросети с насосной подачей насос должен обеспечить напор, равный потребному напору гидросети:

На этом равенстве основан расчет разомкнутой сети с насосной подачей. В одном масштабе строится характеристика насоса Н_нас= f₁(Q) и кривая потребного напора сети Н_потр=f₂(Q).Точка пересечения этих кривых называется рабочей точкой. По этой рабочей точке можно определить, способен ли данный насос обеспечить получение потребного напора при заданном расходе Q.

Полезная мощность насоса равна:

N_п=ρgH_нас·Q=(p₂−p₁)·Q.

Мощность двигателя, приводящего в действие насос, больше полезной мощности насоса на величину затрат мощности на преодоление потерь (потерь на механическое трение, гидравлических потерь, связанных с утечками и перетеканием жидкости из областей с высоким давлением в области с низким давлением через зазоры и т.д.):

N=Nп/η,

где η - общий КПД насоса; η = 0,60 - 0,85 - для шестеренчатых насосов; η = 0,70 - 0,85 - для центробежных насосов.