Курсовая работа.. Алмаз курсавой. РМК Р. Байсеитов атындаы Семей аржыэкономикалы колледжі
 Скачать 70.81 Kb. Скачать 70.81 Kb.
|
|
Қазақстан Республикасының Білім және ғылым министрлігі РМҚК «Р.Байсеитов атындағы Семей қаржы-экономикалық колледжі» КУРСТЫҚ ЖҰМЫС Тақырыбы: Сызықтық емес программалау есебі Орындаған: 4 қ.ВТ тобының оқушысы Әмірбеков Алмаз Тексерген: Вильданова М.Х Қорғаған бағасы: Семей қаласы 2013-2014 оқу жылы Курс жұмысына рецензия Тіркеу номері №_________ Оқушының аты-жөні_______________________________________________ Курсы____________________________________________________________ Бөлім_______________________________________________________________________________________________________________________________ Мамандығы______________________________________________________________________________________________________ пәнінен курс жұмысы Курс жұмысының тақырыбы_________________________________________ _________________________________________________________________ Рецензиялаушы____________________________________________________ ___________________________________________________________________________________________________________________________________ 1.Жұмыстың жетістіктерін талдау: ____________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ (мазмұнының тақырыбына сай келуі, ұсынылған әдебиеттердің, нормативтік материалдардыың пайдалану деңгейі, қаржы жүйесі органдарының жүйесі жұмыс тәжірибиесін есепке алу, мазмұндаудың логикасы мен деңгейі, әрбір сұрқтың ашуының сапасы , т.б. оңды жақтары) 2. Жұмыстың кемшіліктерін талдау: __________________________________ ______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ (тақырыптың ашылмаған немесе жеткілікті түлде толық айтылмаған мәселелерін атап өту, қателер тізімі, басқада кемшіліктерді көрсету) 3.Әдістемелік нұсқаулар мен кеңестер: ________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ (жекелеген обьектілерді, норматитік актілерді т.б. оқу керектігін айту, көрсетілген кемшіліктерді жоюға арнелған кеңестер, жұмысты қорғауға дайындық бойынша нұсқаулар беру, қандай мәселелерге назар аудару керек деген сияқты т.б.) 4.Қорытындылаңдар: _______________________________________________ ________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ __________________________________________________________________ (Жұмыстың қорытынды бағасы, жұмыс мазмұнының жазбаша жұмыстарға қойылатын талаптарға сай келуі, қысқаша қорытынды) Рецензиялаған оқытушы:______М.Х.Вильданова МАЗМҰНЫ
Кіріспе Мен «Өндірістік және экономикалық үрдістерді модельдеу» пәнінен курстық жұмыс орындадым. Курстық жұмысымның тақырыбы «Сызықтық емес программалау есебі» болып табылады. Мен бұл курстық жұмысты орындауды жалпы сұраныс пен тұтынуды талдау арқылы бастадым. Соның ішінде сұраныс пен ұсыныс қисық сызықтарына тоқталып, курстық жұмысымда тұтынудың моделі туралы жазуды ұйғардым. Жалпы бөлім 1.Модель және модельдеу ұғымы 1.1Модель түсінігі және оның түрлері Бастапқы модель деп анықталған жағдайда объектіні алмастыратын қандай да бір көмекші объкті аталған. Сондықтан табиғат заңдарының әмбебаптығы, модельдеудің жалпылығы, жэне біздің білімдерімізді модель түрінде бейнелеудің мүмкідіктері сәйкесіз болды. Мысалы ертедегі философтар табиғи процестерді модельдеу мүмкін емес, табиғи және жасанды процестер түрлі заңдылықтарға бағынады деп санады. Олар табиғатты тек қана логиканыңталқылау әдістерінің, пікір алмасыулардың, яғни замандық терминалогияның, тілдік моделдеудің көмегімен бейнелеуге болады деп жобалады. Ұзақ уақыттар бойына "модель" түсінігі арнайы типтегі материалдық объектілерге ғана, мысалы манекен (адам денесінің моделі), плотинаның кішірейтілген гидродинамикалық моделі, кемелер мен самолеттердің, жануарлардың модельдері ретінде қалыптасты. Уақыт өте келе нақты объектілер жасанды сызбалардың, суреттердің, карталардың модельдік ерекшеліктері арқылы сипаттала бастады. Келесі қадамда модель ретінде нақты объект ғана емес абстрактылы, идеиалдық құрлымдардың да жұмыс істеу мүмкіндіктері белгілі болды. Мұның мысалы математикалық модельдер бола алады. Математика негіздерін зерттеумен айналысаты математиктер мен философтардың еңдектерінің нэтижесінде модельдер теориясы жасалды. Онда модель бір абстрактылы математикалық құрылымның басқасына бейнелеу, түрлендіру нәтижесі болып анықталады. ХХ-ғасырда модель түсінігі нақты және идеалдық модельдерді қатар қамтитындай болып жалпыланды. Сондықтан, абстрактылы модель түсінігі математикалық модельдер шеңберінен шығып, элем туралы білімдер мен танымдардың барлығына қатысты болды. Модель түсінігінің айналасындағы кең талқылаудың қазіргі кезде де жалғасып отырғандығын естен шығармау қажет. Бастапқыда ақпараттық, кибернетикалық бағыттардағы ғылыми пәндер аясында, содан соң ғылымның басқа да салаларында түрлі тәсілдермен іске асырылатын модель ретінде танылды. Негізінде модель мәнін нақтылау тәсілі ретінде қарастырылады. "Модель" термині көп мағыналы. Модель деп қандай да бір заттын кішірейтілген көшірмесін (самолет моделі, тұрғын үйлер макеті), матемаетикалық формулаларды, бұрыштан горизонтқа лақтырылған дененің ұшу моделін, іштен жану двигателі жұмысының моделін, қандай да бір нәрсенің эталоның (метр эталоны, килограмм этолоны) айтамыз. Жалпы түрдегі "модель" түсінігі төмендегідей негізде анықталады . Модель - модельдеу мақсаты тұрғысынан оқып үйренетің объектінің / құбылыстың кейбір жақтарын ұқсастырып бейнелейтін жаңа объект. Модель - объектінің нақты жұмыс істеуіне сәйкестенетін анықталған параметрлер бойынша жұмыс істейтін физикалық/ ақпараттық алмастырушысы. Модельдеудегі ең басты модельдеуші объекті мен оның моделі арасындағы өзара ұқсас қатысы болып табылады. Модель (Model, simulator) 1) қасиеттері белгілі бір мағынадағы жүйенінің немесе процестінқасиеттеріне ұқсас объектілер немесе процестер жүйесі; 2) сериалы бұйымдарды жаппай өндіруге арналған үлгі, эталон; кез-келген бір объекті жұмысы, мыс, процессордың жұмыс істеуін модельдейтін программа немесе құрылғы. Ол материалдық объект түрінде, математикалық байланыстар жүйесі ретінде немесе құрлымды имитациялайтын программа күйінде құрастырылады да, қарастырылатын объектінің жұмыс істеуін зерттеу үшін қолданылады. Модельге қойылатын негізгі талап- оның қасиеттерінің негізгі объектіге сәйкес келуі, яғни барабарлығы. Модельді нақты бар жүйеге алмастыру таңылған, сондықтан ол мынадай бір қатар негізгі талаптар ретін сақтауды қамтамассыз ететіңдей модель болуы қажет; 1)есеп қойылымының айқындылығы, қойылған мақсат жүйенің негізгі элементерінің құрамымен сапалық сипатамаларын анықтайды. 2) қатаң математикалық тәуелділік негізінде қандай да шешімдерді табуға байланысты есептер орындалуын қамтамасыз ететін формальді түрдегі өзара байланыстар көрсетілімнің міндеттілігі. 3)модельдерді жеңілдетудің мақсатты дәрежесі. 4) алынатын нәтиже нақтылығы, онымен жұмыс жасаудың қауіпсіздігін сипаттайтын модельдердің қажетті сенімділігін қамтамассыз ету. 5)модельге тек негізгі элементтерді қосу және таңдау олардың арасындағы өзара тәуелділікті құруды анықтайтын қойылған мақсатпен сәйкестігі . Көрсетілген талаптарды бір-бірінен бөлінген және өз бетінше әрекет етуші түрінде қарастыруға болмайды . Тек қана олардың кешенді есебі үлгі сапасы мен нәтиже көмегімен алынган негіздерге сүйенеді. Тәжірбиеде қолданылып жүрген үлгілерді шартты түрде екіге бөлуге болады: физикалық және символдық. Өз кезегінде физикалық үлгілердің ішінде геометриялық ұқсастық модельдері мен модель-аналогты болады. Геометриялық ұқсастық модельдерді негізінен тұпнұсқалық геометриялық сипаттамалары ман құрылымдарын кескіндейді. Мұндай модельдер бір немесе сондай физикалық жараласында тұпнұсқамен сыртқы ұқсастықты сақтайды. Модельдердің өлшемі теңбе-тең түрде азайтылған немесе тұпнұсқамен салыстырғанда үлкейтілген болуы мүмкін. Геометриялық ұқсастық модельдерінің артықшылығы, біріншіден күрделі қымбат тұратын жүйелерді сараптама өткізу немесе экономикалық тиімді еместерді оларға ендіруді мумкіндіктері , екіншіден , күрделі түрде алынатын арнайы жүйедегі құрылым мен функциялар туралы түсінігі болуы, үшіншіден, алынған нәтиженің нақтылығы. Геометриялық ұқсастық модельдердің негізгі кемшіліктеріне мыналар жатады: Әрбір зерттелетін жүйелер үшін құрал мен уақыттың үлкен шығындарына байланысты ескіге қайта жасақталатын немесе жаңа модель құруды қажет етеді; Модельдің бұл түрі жүйе динамкасын зерттеу үлгілері үшін нашар лайықталған. Математикалық модель сызушы құрылым мен нақты жүйе функциясының математикалық және логикалық қатысы жүйесін қамтиды. Математикалық модель өзінің физикалық жаратылысы жағынан түпнұсқадан ерекшеленеді. Түпнұсқа қасиетін зерттеуді математикалық модельдер көмегімен жүргізу ыңғайлы, арзан және физикалық үлгілеумен салыстырғанда уақыт аз кетеді. Көптеген математикалық модельдер жан-жақты болып келеді, олар әр түрлі жүйелерді зерттеуге пайдалану мүмкіндігі болады. 1.2Модельдеу. Математикалық есептерді модельдеу Негізігі ғылыми таным әдістерінің біріне сараптама жатады, ал оның ең таратылған әр түрлілігі - жүйелерді модельдеу әдісі. Модельдеу (моделирование; simulation) - кез-келген құбылыстардың, процестердің немесе объект жүйелерінің қасиеттері мен сипаттамаларын зерттеу үшін олардың үлгісін құру (жасау) және талдау; бар немесе жаңадан құрастырылған объектілердің сипатын анықтау немесе айқындау үшін олардың аналоктарында (модельде) объектілердің әр-түрлі табиғатың зеттеу әдісі. Модель төрт денгейде түпнұсқанын гноселогиялық орынбасары бола алады: 1 - элеметтер денгейінде, 2 - құрлым деңгейіде, 3 - қалып - күй немесе қызметік деңгейін, 4 – нәтижелер деңгейінде. Сипаты бойынша модельдеу объектінің геометриялық, физикалық, динамикалық және қызметтік сипатын нақты дәл береді. Идеалдық моделдеуге объектінің ойдағы бейнесі жатады. Ойша модельдеу тіл көмегімен іске асырылады. Компьютерлік модельдеу — бұл да оқып үйренетін объекті теориясының модельденуі. Өндірістік және экономикалық процестерді модельдеу – процестерді процестер құрылымын кескіндейтін, ақпараттар ағыны мен объектілерді сипаттайтын модель құру жолымен зерттеу. Модельденетін жүйе элементтерінің сапасына процедуралар, ал модельдеу объектісі жүйе болса, онда көрсеткіштер мен белгілер әсер етуі мүмкін. Модельдеу үш элементтен тұрады: Субъект, мұнда адам зерттеуші қатысады; Зерттеу объектісі(жүйелер); Объект моделі(жүйелер), бұл объекті мен субъектіні байланыстырушы аралық. Модельдеудің негізгі проблемаларының бірі ретінде түпнұсқа және модель дәрежесін анықтауды көрсетуге болады. Түпнұсқа және модельдер рөлінде болатын жүйелер әр түрлі және өзара толық ұқсас болуы мүмкін емес. Негізінде модельдеуде түпнұсқаның барлық сипаттары бейнеленбейді, тек қана сипаттамалық топтағылар анықталады. Модельдеу субъектісі. Модельдеуші (модель субьектісі) тек адам бола алады. Модельдеу объектісі табиғи (өсімдік, күн жүйесі және адамның ықпалымен құрылып жасанды болуы мүмкін. Объекттуралы есептіқажетті ақпарат.Модельдеу жүйесі (modeling system) - зертелетін жүйенің немесе оның элементтерінің математикалық және физикалық анологтарын құру және талдау. Модельдік тәжірибе зерттеу тәсілі реттінде жүйенің жанғыртуға және зерттеуге мүмкіндік береді, ал зерттелетін жүйеге тікелей тәжірбие жүргізу қиын, немесе экономикалық түрғыдан тиімсіз болуы мүмкін. Табиғи объектілерді ешқандай модельдің толықтай бейнелей алмайтындығы белгілі. Табиғи объектілердің элементтерінің арасындағы байланыстардың көбінесе белгісіз болуы олардың күрделілігін айқындайды. Сондықтан табиғи объектілердің модельдері түпнүсқаға қарағанда қарапайым болады. Адамдар тарапынан құрылатын объектілерде мұндай жағдайлардың толық ескерілмеуі мүмкін. Бірақ модельдеу барысында модельдеу мақсаты тұрғсынан қажетсіз детальдар еленбейді. Практикалық есепті шешу тұрғысынан модельдерді пайдалану оқып үйренетін объектілердегі модельдеудің мәнін, мазмұнын демострациялауға мүмкіндік береді. 1.3. Модельдеудің жалпы схемасы  МОДЕЛЬ        Объект туралы есепті шешуге қажетті ақпарат Модельдеу субъектісі Модельдеу объектісі    Есеп қойылымы Негізгі бөлім 2.Есептің жалпы қойылуы Жалпы математикалық программалау есептерінің математикалық моделінің жазылу жолы бір типтес. Мысалы, мына шектеулер жүйелерін қанағаттандыратын: 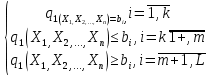 және 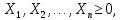 (сонымен қатар (сонымен қатар 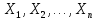 - бүтін сандар болуы мүмкін) мына функцияны - бүтін сандар болуы мүмкін) мына функцияны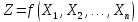 экстремалдық мәніне жеткізетін 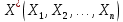 – векторын табу керек деп жазылатыны белгілі. – векторын табу керек деп жазылатыны белгілі.Көрсетілген жағдайларды қанағаттандырмайтын кез-келген математикалық программалау есептері сызықты емес программалау есебі деп аталады. Сызықты емес программалау (СЕП) есептерінің сипаты және дәрежелері сызықты программалау есептеріне қарағанда кеңірек және жоғары. СЕП есептері тауар қорларын басқаруда, құрал-жабдықтарды жөндеу жұмыстарын ұйымдастырғанда, халық шаруашылығы кәсіпорындарының өндірістеріне болжаулар жасағанда және т.б. халық шаруашылық есептерінде қолданылады. Жалпы СЕП есептерінің мәнісі функцияның: 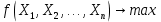 немесе 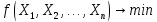 максималды немесе минималды мәнін анықтауда. Сонымен қатар, егер Z-функциясы n-функциялардың (∑) қосындысы болса, онда 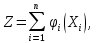 оны «Сепарабельді» немесе егер 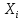 -ң біреуі екінші (шаршы) дәрежелі болса, онда оны шаршыланған (квадратическая) деп атайды. Екі жағдайда да мақсат функцияның экстремалдық мәні мына шарттарда: -ң біреуі екінші (шаршы) дәрежелі болса, онда оны шаршыланған (квадратическая) деп атайды. Екі жағдайда да мақсат функцияның экстремалдық мәні мына шарттарда: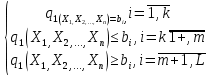 және 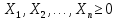 ізделінеді. СЕП есептерінің СП есептерінен айырмашылығы, олардың бәріне бірдей шешу әдістері жоқ және шешімі мүмкін бола алатын аймақ (ШМБА) барлық уақытта дөңес болған кездің өзінде мақсат функцияның бірнеше локалды экстремалды мәндері болуы мүмкін. Мұндай кезде әртүрлі есептеу әдістерімен локалды экстремалды мәндерді беретін нүктелерді табуға болады, бірақ осы мәндердің ішінен глобалды (абсолюттік, ең төменгі немесе ең жоғарғы) экстремалдық мәнді анықтау ең қиын іс және бірден оны анықтау мүмкін емес. Мақсат функцияның және шектеулер жүйелерінің түріне байланысты СЕП есептерін шешу үшін бірнеше арнайы әдістер жасалынған. Оларға Лагранж әдісі, графиктік әдіс, шаршы(квадраттық) және дөңес программалау, градиент әдістері және жуықталған әдістер жатады. Егер СП есебінің экстремалды нүктесі көпжақтылардың төбелерінде болса, ал СЕП есептерінің экстремалды нүктелері көпжақтылардың төбелерінде немесе қабырғаларында, немесе қырында, немесе осы дененің ішінде жатуы мүмкін. Егер СЕП есебінде сызықсыз шектеулер болса, онда шешімі бола алатын аймақ дөңес болмайды және глобалдық оптимумнан (ең кіші немесе ең үлкен) басқа, локалдық оптимум (ең кіші емес немесе ең төмен емес) болуы мүмкін. СЕП есебін шешу алгоритмін нақтылы тұжырымдау үшін бірнеше мысалдар мен тәсілдерді қарастырамыз. 2.1.Есептің графиктік әдісі. СЕП есебін геометриялық жолмен шешу мынадай кезеңдерден тұрады: 1.(8.3)қатынаспен анықталған, есептің шешімі мүмкін бола алатын аймақты табады(егер ол бос болса, онда есептің шешімі жоқ). 2. 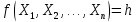 - гипержазықтығы құрылады. - гипержазықтығы құрылады.3.Гипержазықтықтың ең биік (ең төменгі) деңгейі анықталады немесе есептің көптік шешімі бола алатын аймақта мақсат функцияның шектеулеріне байланысты шешімі жоқ екендігі анықталынады. 4. Гипержазықтықтың ең биік (ең төменгі) деңгейі өтетін, шешімі мүмкін бола алатын аймақтан бір нүкте табылады және сол нүктеде функция (8.3) мәні анықталынады. Мысал. 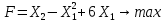 мына жағдайда: 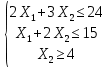 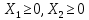 Координаттар өсінде (8.7) жүйедегі теңсіздіктердің графиктерін тұрғызайық. Берілген есептің шешімі мүмкін бола алатын аймақ ОАВС көпбұрышы. Осы аймақтан функция максималды мәнге жететін нүктені анықтайды. Ол үшін деңгей сызықты 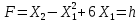 тұрғызамыз. Мұндағы h – кез келген тұрақты шама, осы көрсеткіштің әртүрлі мәнінде функция қалай өзгеретінін зертейік.h-ң әр мәнінде парабола аламыз. Ол ОХ осіне қашықтаған сайын h-ң мәні өседі. ОАВС қырының бірінде парабола жанасқан жерінде функция (8.6) максималды мәніне жетеді. Сонымен (8.6)-(8.8) есебін шығарудың нәтижесінде мақсат функцияның максималды мәні көпбұрыштың төбесінде емес екеніне көзіміз жетті. Сондықтан, сызықты программалау есебінің геометриялық шығару жолын, яғни көпбұрыштың барлық төбелерін қарап шығу тәсілін бұл есепке қолдануға болмайды. Мақсат функциясы сызықты және шектеулер жүйесіндегі теңсіздіктер сызықтық емес СЕП есебін қарастырайық Мысал.Мақсат функцияның 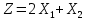 мына жағдайда: 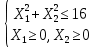 глобалдық (абсолюттік) экстремалды мәнін табу керек. Шешімі:Шешімі мүмкін бола алатын аймақ радиусы 4-ке тең шеңбердің төрттен бір бөлігі, ол координаттар өсінің бірінші ширегінде орналасқан. Деңгей сызығын 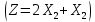 өз-өзіне паралеллді жылжытып отырып, шеңбермен жанасу нүктесіне деін апарамыз.Суретте деңгей сызығы шеңбермен А нүктесінде жанасқан. Деңгей сызығы өз-өзіне паралеллді жылжытып отырып, шеңбермен жанасу нүктесіне деін апарамыз.Суретте деңгей сызығы шеңбермен А нүктесінде жанасқан. Деңгей сызығы 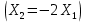 бұрыштық коэффициенті -2-ге тең. Функция глобалдық минимумына О(0,0) нүктесінде, ал глобалдық максимумы оның шеңбермен жанасу нүктесінде жетеді. бұрыштық коэффициенті -2-ге тең. Функция глобалдық минимумына О(0,0) нүктесінде, ал глобалдық максимумы оның шеңбермен жанасу нүктесінде жетеді. 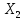 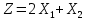   A A C  0 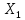 А нүктесі арқылы деңгей сызығына перпендикуляр жүргіземіз. Бұл тік бұрышты сызық координаттың бас нүктесі арқылы өтеді және оның бұрыштық коэффициенті 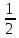 тең, сонымен қатар ол мынадай теңдікпен өрнектелінеді: тең, сонымен қатар ол мынадай теңдікпен өрнектелінеді: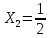 Нәтижесінде мынадай теңдіктер жүйесі табылады: 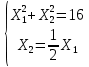 Жүйені шешу нәтижесінде 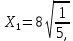 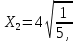 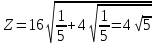 Сөйтіп, глобалды максимумде мақсат функция 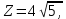 ал сол нүктенің координаты ал сол нүктенің координаты A 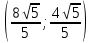 2.2.Лагранж көбейткіштер әдісі Айталық, мына шектеулерде 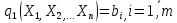 мынадай функцияның экстремалдық мәні ізделінсін. 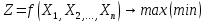 . .Шектеулер теңдеу түрінде берілгендіктен, оларды шешу үшін, бірнеше айнымалылардан тұратын функцияның экстремалдық мәнін іздейтін белгілі классикалық әдісті қолдануға болады. Бұл кезде 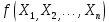 Және 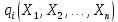 функциялар өздерінің жекешеленген туындылармен бізге үздіксіз деп есептелінеді. Есептің шешімін табу үшін қосымша 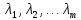 айнымалылар енгізіледі. Бұл айнымалыларды Лагранж көбейткіштері деп атайды. Нәтижесінде Лагранж функциясы құрылады. айнымалылар енгізіледі. Бұл айнымалыларды Лагранж көбейткіштері деп атайды. Нәтижесінде Лагранж функциясы құрылады.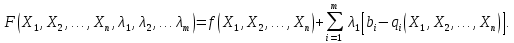 Функциядан жекелеген туындылар алынады: 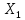 бойынша бойынша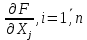 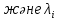 бойынша бойынша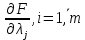 Қорытындысында 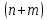 -нен тұратын теңдеулер жүйесі тұрғызылады. -нен тұратын теңдеулер жүйесі тұрғызылады.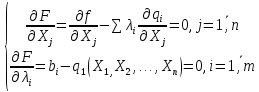 Осы жүйені шешу нәтижесінде 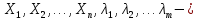 табылады. табылады.Сонымен, СЕП есебін Лагранж көбейткіші арқылы шығару жұмысы мынадай кезеңдерден тұрады. 1.Лагранж функциясы құрылады. 2.Лагранж функциясынан 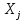 және және 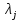 бойынша жекеленген туынды алынады да, теңдеулерді нөлге теңестіреді. бойынша жекеленген туынды алынады да, теңдеулерді нөлге теңестіреді.3.Тұрғызылған теңдеулер жүйесін шешу арқылы, мақсат функция экстремалды мәніне жететін нүктелерді табады. Теңдеулер жүйесінің бірнеше шешімдері болуына байланысты Лагранж әдісін қолдану шектеулі. Мысал. 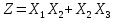 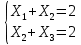 Шешуі: Лагранж функциясын тұрғызамыз: 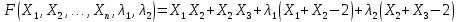 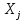 және және 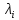 бойынша жекеленген туынды алынып, теңдікті нөлге теңестіріп жазып, мынадай теңдіктер жүйесін аламыз. бойынша жекеленген туынды алынып, теңдікті нөлге теңестіріп жазып, мынадай теңдіктер жүйесін аламыз.Есеп. Кәсіпорындар 180 бұйым дайындамақшы. Бұл бұйымдар екі түрлі технологиялық тәсілмен, әр түрлі шығынмен дайындалуы мүмкін. Егер 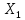 -бұйым 1-тәсілмен жасалынатын болса, онда шығын мына заңдылықпен өзгереді: -бұйым 1-тәсілмен жасалынатын болса, онда шығын мына заңдылықпен өзгереді: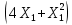 теңге, ал 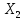 -бұйым 2-тәсілмен жасалынса, онда шығын: -бұйым 2-тәсілмен жасалынса, онда шығын:Қорытынды Қорыта келе, жалпы модель дегеніміз танып білу процесінде объект оригиналдың орнына ұсынылатын, оның басты қасиеттерін сақтайтын материялдық және ой түріндегі объект немесе үлгі болып табылады. h –ң әр мәнінде парабола аламыз. Ол ОХ осінен қашықтаған сайын h-ң мәні өседі. ОАВС қырының бірінде парабола жанасқан жерінде функция (8.6) максималды мәніне жетеді. Пайдаланылған әдебиеттер: 1. Вентцель Е.С. Исследование операций. – М., «Советское радио», 1972. - 552 с. 2. Вентцель Е.С. Элементы динамического программирования. – М.: Наука, 1964. 3. Коршунов Ю.М. Математические основы кибернетики: Учебное пособие для вузов. – 2-е изд., переаб. и доп. – М.: Энергия, 1980. – 424 с. 4. Акулич И.Л. Математичское программирование в примерах и задачах. Учебное пособие . – М.: Высшая школа, 1986. – 319 с. 5. Кубонива М. Математическая экономика на персональном компьютере. – М.: Финансы и стаистика, 1991. – 304 с. 6. Ефимов А.К., Куралбаев З.К., Харасахал В.В., Рахимбаев А.Р. Экономико-математические модели и методы. – Алматы: КазГАСА, КИЭП, 1999. – 127 с. 7. Куралбаев З.К. Решение задач по математическому программированию (на казахском и русском языках).- Алматы: РИК МО РК, - 1997. |
