Родионова Наталья Евгеньевна Донской, 2019 Содержание Введение в 2003 году было принято решение
 Скачать 95.59 Kb. Скачать 95.59 Kb.
|
|
Городская научно – практическая конференция учащихся «Талант. Мысль. Открытие» Проблемно–поисковая работа Элементы комбинаторики и теории вероятности в задачах ОГЭ и ЕГЭ Выполнена учеником 9 класса «А» МБОУ «Гимназия № 20» Малаховым Александром Андреевичем Руководитель учитель математики Родионова Наталья Евгеньевна Донской, 2019 Содержание Введение В 2003 году было принято решение о включении элементов теории вероятностей и статистики в школьный курс математики общеобразовательной школы. Но к этому времени элементы теории вероятностей и статистики уже более десяти лет в разрозненном виде присутствовали в известных школьных учебниках алгебры для разных классов (Дорофеева Г.В., Виленкина Н.Я., Мордковича А.Г.) и в виде отдельных учебных пособий. Изучали ее только в лицеях и гимназиях. На сегодняшний день теория вероятности изучается в 9 классе, но в силу возрастных особенностей школьников не может быть полностью освоена. Далее этому вопросу не уделяется значительного внимания. В программе по математике 10-11 классов теория вероятности изучается только в последней главе и на самом простом уровне. Поэтому учащиеся не умеют решать сложные задачи на вероятность и задачи повышенной трудности. Однако такие задачи необходимо уметь решать, т.к.: В ОГЭ (№9) и ЕГЭ (профиль №4, база №11) по математике включены задачи на применение теории вероятности; Понятие вероятность широко используется не только в науке, но и в реальной жизни. В связи с этим передо мной встала проблема: при помощи дополнительной литературы изучить теоретические основы теории вероятности и комбинаторики; учиться применять эти знания при решении задач. Целью работы является изучение основ теории вероятностей и комбинаторики, знакомство с видами задач на вероятность в заданиях открытого банка задач по математике ОГЭ и ЕГЭ 2019 и их решение. Методы исследования: поисковый метод с использованием научной и учебной литературы, интернета; исследовательский метод при определении видов задач, их решения различными способами; практический метод решения задач; анализ полученных в ходе исследования данных. Теоретическая значимость работы заключается в том, что собранные теоретические материалы могут быть использованы на занятиях элективных курсов и кружков по математике при подготовке к экзамену. Практическая значимостьпроектно-исследовательской работы заключается в создании базы решенных задач ОГЭ и ЕГЭ. Глава 1. Теоретическая часть 1.1 Элементы комбинаторики Факториал натурального числа 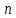 определяется по формуле определяется по формуле  . Также считается, что . Также считается, что 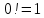 . .Размещением из 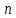 элементов множества элементов множества 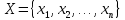 по по 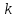 элементам назовем любой упорядоченный набор элементам назовем любой упорядоченный набор 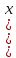 ) элементов множества Х. ) элементов множества Х.Если допускаются повторения, то число размещений из 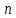 элементов по элементов по 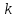 с повторениями находится по формуле с повторениями находится по формуле 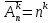 . .Если же выбор делается без повторений, т.е. каждый элемент множества 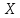 можно выбирать только один раз, то количество размещений из можно выбирать только один раз, то количество размещений из 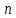 элементов по элементов по 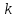 без повторений определяется равенством без повторений определяется равенством 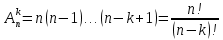 . .Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр. Если цифры повторяются, то количество трехзначных чисел равно 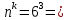 216. Если цифры не могут повторяться, то количество чисел равно 216. Если цифры не могут повторяться, то количество чисел равно 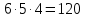 Частный случай размещения при 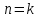 называется перестановкой из называется перестановкой из 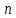 элементов. Число всех перестановок из элементов. Число всех перестановок из 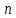 элементов равно элементов равно 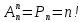 . .Пример. 30 книг стоит на книжной полке, из них 27 различных книг и одного автора три книги. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом? Будем считать три книги одного автора за одну книгу, тогда число перестановок будет 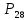 . А три книги можно переставлять между собой . А три книги можно переставлять между собой 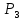 способами, тогда искомое число способов равно способами, тогда искомое число способов равно 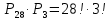 . .Пусть теперь из множества 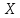 выбирается неупорядоченное подмножество выбирается неупорядоченное подмножество 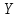 (порядок элементов в подмножестве не имеет значения). (порядок элементов в подмножестве не имеет значения).Сочетаниями из 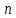 элементов по элементов по 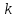 называются подмножества из называются подмножества из 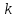 элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из из элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из из 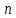 элементов по элементов по 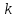 равно равно 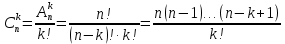 . .Справедливы равенства: 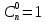 , , 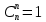 , , 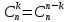 . .Пример. В группе из 27 студентов нужно выбрать трех дежурных. Сколькими способами можно это сделать? Так как порядок не важен, то это сочетания: 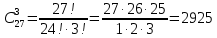 . .Правило суммы. Если некоторый объект  может быть выбран из совокупности объектов может быть выбран из совокупности объектов 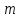 способами, а другой объект способами, а другой объект  может быть выбран может быть выбран 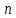 способами, то выбрать либо способами, то выбрать либо  , либо , либо  можно можно 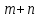 способами. способами.Правило произведения. Если объект  можно выбрать из совокупности объектов можно выбрать из совокупности объектов 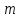 способами и после каждого такого выбора объект способами и после каждого такого выбора объект  можно выбрать можно выбрать 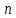 способами, то пара объектов способами, то пара объектов 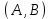 в указанном порядке может быть выбрана в указанном порядке может быть выбрана 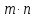 способами. способами.Пример. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка? По принципу умножения получается 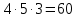 нарядов (комбинаций). нарядов (комбинаций).1.2 Классическое определение вероятности Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Пример. Попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием. Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может. Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе. Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события  , если появление этого события влечет за собой появление события , если появление этого события влечет за собой появление события  . .Вероятностью события  называют отношение числа называют отношение числа 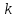 благоприятствующих этому событию исходов к общему числу благоприятствующих этому событию исходов к общему числу 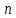 всех равновозможных несовместных элементарных исходов, образующих полную группу: всех равновозможных несовместных элементарных исходов, образующих полную группу: 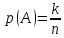 . .Свойство 1. Вероятность достоверного события равна единице. Свойство 2. Вероятность невозможного события равна нулю. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 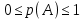 . .Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10? Пусть событие  = (Номер вынутого шара не превосходит 10). Этому событию благоприятвует 10 исходов. Следовательно, = (Номер вынутого шара не превосходит 10). Этому событию благоприятвует 10 исходов. Следовательно, 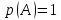 . Событие . Событие  достоверное. достоверное.Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые? Вынуть два шара из десяти можно следующим числом способов 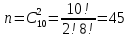 . Число случаев, когда среди этих двух шаров будут два белых, равно . Число случаев, когда среди этих двух шаров будут два белых, равно 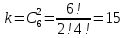 . Искомая вероятность равна . Искомая вероятность равна 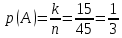 Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар? Так как синих шаров в урне нет, то 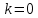 , , 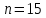 . Следовательно, искомая вероятность . Следовательно, искомая вероятность 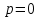 . Событие, заключающееся в вынимании синего шара, невозможное. . Событие, заключающееся в вынимании синего шара, невозможное.1.3 Геометрическое определение вероятности Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область 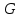 (на прямой, плоскости или пространстве). Геометрическая вероятность события (на прямой, плоскости или пространстве). Геометрическая вероятность события  (попадание в некоторую подобласть (попадание в некоторую подобласть 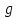 облаcти облаcти 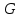 ) определяется отношением: ) определяется отношением: 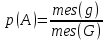 , где , где 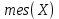 – мера области – мера области 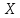 (ее длина, площадь или объем). (ее длина, площадь или объем).Пример. Попадаем в квадратную мишень. В квадрат вписан круг. Определить вероятность попадания именно в круг мишени. Пусть сторона квадрата равна 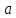 , тогда радиус круга , тогда радиус круга 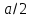 . Мерой являтся площадь фигур. . Мерой являтся площадь фигур. 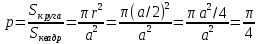 . .1.4 Статистическое определение вероятности Относительной частотой события  (или просто частотой) определяется формулой (или просто частотой) определяется формулой 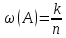 , где , где 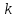 – число опытов, в которых появилось событие – число опытов, в которых появилось событие  , , 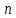 – число всех проведенных опытов. – число всех проведенных опытов.Вероятностью события называется число, около которого группируются значения относительной частоты данного события в различных сериях большого числа испытаний. 1.5 Сложение и умножение вероятностей Событие  называется частным случаем события называется частным случаем события  , если при наступлении , если при наступлении  наступает и наступает и  . . События  и и  называются равными, если каждое из них является частным случаем другого. Равенство событий называются равными, если каждое из них является частным случаем другого. Равенство событий  и и  записываем записываем 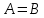 . .Суммой событий  и и  называется событие называется событие 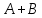 , которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: , которое наступает тогда и только тогда, когда наступает хотя бы одно из событий:  или или  . .Произведением событий  и и  называется событие называется событие 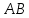 , которое наступает тогда и только тогда, когда наступают оба события: , которое наступает тогда и только тогда, когда наступают оба события:  и и  одновременно. одновременно. Случайные события  и и  называются несовместными, если при данном испытании не могут наступить оба события (может наступить только одно из них). называются несовместными, если при данном испытании не могут наступить оба события (может наступить только одно из них).Случайные события  и и  называются совместными, если при данном испытании могут произойти оба эти события. называются совместными, если при данном испытании могут произойти оба эти события.Теорема о сложении вероятностей 1. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий: 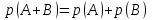 . .Если случайные события 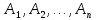 образуют полную группу несовместных событий, то имеет место равенство образуют полную группу несовместных событий, то имеет место равенство 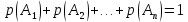 . .Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле 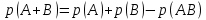 . .События  и и  называются независимыми, если появление одного из них не меняет вероятности появления другого. называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие  называется зависимым от события называется зависимым от события  , если вероятность события , если вероятность события  меняется в зависимости от того, произошло событие меняется в зависимости от того, произошло событие  или нет. или нет.Теорема об умножении вероятностей. Вероятность произведения независимых событий  и и  вычисляется по формуле: вычисляется по формуле: 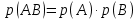 . .Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный. Обозначим события:  – вынули белый шар из первого ящика, – вынули белый шар из первого ящика, 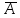 – вынули черный шар из первого ящика: – вынули черный шар из первого ящика: 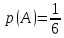 , , 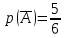 . Аналогично . Аналогично  – вынули белый шар из второго ящика, – вынули белый шар из второго ящика, 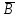 – вынули черный шар из второго ящика: – вынули черный шар из второго ящика: 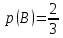 , , 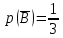 . Нам нужно, чтобы произошло одно из событий . Нам нужно, чтобы произошло одно из событий 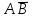 или или 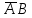 . По теореме об умножении вероятностей . По теореме об умножении вероятностей 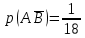 , , 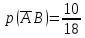 . Тогда искомая вероятность по теореме сложения будет . Тогда искомая вероятность по теореме сложения будет 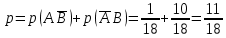 . .Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания. Пусть  – попадание первого стрелка, – попадание первого стрелка, 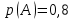 ; ;  – попадание второго стрелка, – попадание второго стрелка, 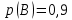 . Тогда . Тогда 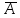 - промах первого, - промах первого, 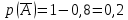 ; ; 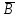 - промах второго, - промах второго, 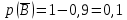 . Найдем нужные вероятности. а) . Найдем нужные вероятности. а) 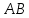 – двойное попадание, – двойное попадание, 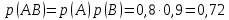 ; б) ; б) 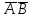 – двойной промах, – двойной промах, 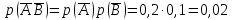 ; в) ; в) 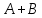 – хотя бы одно попадание, – хотя бы одно попадание, 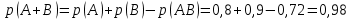 ; г) ; г) 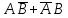 – одно попадание, – одно попадание, 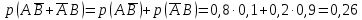 . .Пусть в результате испытания могут появиться 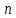 событий, независимых в совокупности, либо некоторые из них, причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема. событий, независимых в совокупности, либо некоторые из них, причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.Теорема. Вероятность появления хотя бы одного из событий 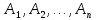 , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 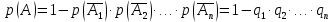 . Если события . Если события 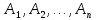 , имеют одинаковую вероятность , имеют одинаковую вероятность 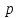 , то формула принимает простой вид: , то формула принимает простой вид: 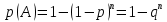 . .Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: 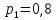 ; ; 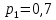 ; ; 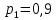 . Найти вероятность хотя бы одного попадания (событие . Найти вероятность хотя бы одного попадания (событие  ) при одном залпе из всех орудий. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события ) при одном залпе из всех орудий. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 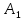 (попадание первого орудия), (попадание первого орудия), 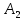 (попадание второго орудия) и (попадание второго орудия) и 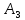 (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям (попадание третьего орудия) независимы в совокупности. Вероятности событий, противоположных событиям 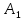 , , 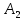 и и 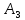 (т. е. вероятности промахов), соответственно равны: (т. е. вероятности промахов), соответственно равны: 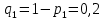 , , 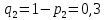 , , 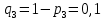 . Искомая вероятность . Искомая вероятность 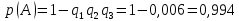 . .Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие  ). Пусть ). Пусть 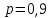 – вероятность того, что машина работает, тогда – вероятность того, что машина работает, тогда 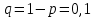 – вероятность того, что машина не работает. Искомая вероятность – вероятность того, что машина не работает. Искомая вероятность 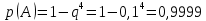 . .1.6 Условная вероятность Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких ограничений, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события  при дополнительном условии, что произошло событие при дополнительном условии, что произошло событие  . .Условной вероятностью 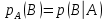 называют вероятность события называют вероятность события  , вычисленную в предположении, что событие , вычисленную в предположении, что событие  уже наступило. уже наступило.Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е. 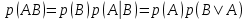 . .В частности, отсюда получаем 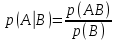 . .Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие  – появление белого шара при первом вынимании. Событие – появление белого шара при первом вынимании. Событие  – появление белого шара при втором вынимании. Очевидно, что вероятность события – появление белого шара при втором вынимании. Очевидно, что вероятность события  , если событие , если событие  произошло, будет произошло, будет 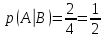 . Вероятность события . Вероятность события  при условии, что событие при условии, что событие  не произошло, будет не произошло, будет 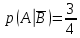 . .1.7 Формула полной вероятности и формула Байеса Если событие  может произойти только при выполнении одного из событий может произойти только при выполнении одного из событий 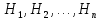 , которые образуют полную группу несовместных событий, то вероятность события , которые образуют полную группу несовместных событий, то вероятность события  вычисляется по формуле вычисляется по формуле 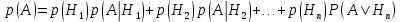 . Эта формула называется формулой полной вероятности. . Эта формула называется формулой полной вероятности.Вновь рассмотрим полную группу несовместных событий 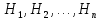 , вероятности появления которых , вероятности появления которых  . Событие . Событие  может произойти только вместе с каким-либо из событий может произойти только вместе с каким-либо из событий  , которые будем называть гипотезами. Если событие , которые будем называть гипотезами. Если событие  произошло, то это может изменить вероятности гипотез: произошло, то это может изменить вероятности гипотез:  . .Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез  называются апостериорными вероятностями, тогда как называются апостериорными вероятностями, тогда как 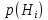 - априорными вероятностями. - априорными вероятностями.Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта. Обозначим через  событие, заключающееся в том, что будет куплена продукция высшего сорта, через событие, заключающееся в том, что будет куплена продукция высшего сорта, через 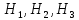 обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям. Можно применить формулу полной вероятности: обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям. Можно применить формулу полной вероятности: 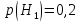 ; ; 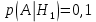 ; ; 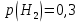 ; ; 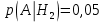 ; ; 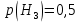 ; ; 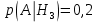 . Подставляя эти значения в формулу полной вероятности, получим искомую вероятность: . Подставляя эти значения в формулу полной вероятности, получим искомую вероятность: 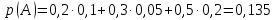 . .1.8 Независимые испытания. Формула Бернулли При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли. Пример повторных испытаний: многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну. Итак, пусть в результате испытания возможны два исхода: либо появится событие  , либо противоположное ему событие. Проведем , либо противоположное ему событие. Проведем 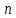 испытаний Бернулли. Это означает, что все испытаний Бернулли. Это означает, что все 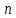 испытаний независимы; вероятность появления события испытаний независимы; вероятность появления события  в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события  в единичном испытании буквой в единичном испытании буквой 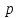 , т.е. , т.е. 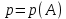 , а вероятность противоположного события - буквой , а вероятность противоположного события - буквой 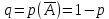 . .Тогда вероятность того, что событие  появится в этих появится в этих 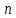 испытаниях ровно испытаниях ровно 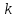 раз, выражается формулой Бернулли: раз, выражается формулой Бернулли: 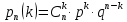 , где , где 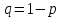 . .Пример.В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых. Событие  – достали белый шар. Тогда вероятности – достали белый шар. Тогда вероятности 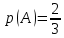 , , 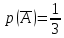 . По формуле Бернулли требуемая вероятность равна . По формуле Бернулли требуемая вероятность равна 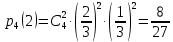 . . |
