Родионова Наталья Евгеньевна Донской, 2019 Содержание Введение в 2003 году было принято решение
 Скачать 95.59 Kb. Скачать 95.59 Kb.
|
|
15 (320199). Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов – математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов – математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку – 0,8, по иностранному языку – 0,7 и по обществознанию – 0,5. Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей. Решение: Пусть M, P, O, U- вероятность того, что абитуриент З. сдаст математику, русский язык, обществознание и иностранный язык соответственно на 70 или более баллов, их вероятности в том же порядке 0,6; 0,8; 0,5 и 0,7. Сдача каждого экзамена не зависима друг от друга, а поступления на одну из специальностей являются совместными, поэтому 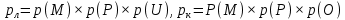 , где , где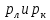 - вероятности поступление на «Лингвистику» и «Коммерцию». Искомая вероятность равна: - вероятности поступление на «Лингвистику» и «Коммерцию». Искомая вероятность равна: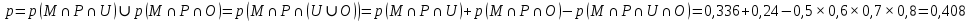 Ответ: 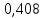 16 (320176). Вероятность того, что электрический чайник прослужит больше года равна 0,97. Вероятность того, что он прослужит больше двух лет равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. Решение: Пусть p – вероятность того, что чайник прослужит больше года, но меньше двух лет, 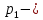 больше года, больше года,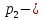 больше двух лет. Так как события больше года, но меньше двух и больше двух лет не совместны, а также в сумме дают событие больше года, то больше двух лет. Так как события больше года, но меньше двух и больше двух лет не совместны, а также в сумме дают событие больше года, то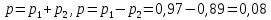 Ответ: 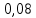 17 (319353). Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45% этих стёкол, вторая – 55%. Первая фабрика выпускает 3% бракованных стёкол, а вторая - 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Решение: Пусть событие B – куплено бракованное стекло. Обозначим через 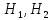 события, заключающиеся в покупке продукции первой и второй фабрики соответственно. Можно применить формулу полной вероятности: события, заключающиеся в покупке продукции первой и второй фабрики соответственно. Можно применить формулу полной вероятности: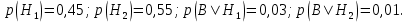 Подставляя эти значения в формулу полной вероятности получим искомую вероятность Подставляя эти значения в формулу полной вероятности получим искомую вероятность 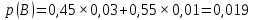 Ответ: 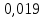 18 (320177). Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что купленное у этой агрофирмы яйцо окажется из первого хозяйства. Решение: Событие B – яйцо высшей категории, событие H1 – яйцо из 1 хозяйства, событие H2 – яйцо из 2 хозяйства. Пусть p(H1)=x, тогда p(H2)=1-x, тогда 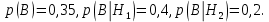 По формуле полной вероятности, вероятность покупки яйца высшего сорта равна: По формуле полной вероятности, вероятность покупки яйца высшего сорта равна: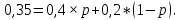 Решая данное уравнение, получаем Решая данное уравнение, получаем 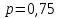 Ответ: 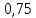 19 (320211). Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля. Решение: Пусть событие З означает, что батарейка забракована системой контроля. Это могло произойти, если по ошибке «отсеяна» качественная продукция или система контроля сработала правильно. Событие Н – батарейка неисправная, p(Н)=0,02. Событие Х – батарейка исправная, p(Х)=1-0,02=0,98. Событие ЗН – забракована неисправная, p(ЗН)=0,99. Событие ЗX – забракована хорошая, p(ЗХ)=0,01. По формуле полной вероятности, вероятность забраковки батарейки равна: 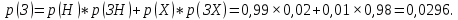 Ответ: 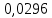 20 (320212). На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D. 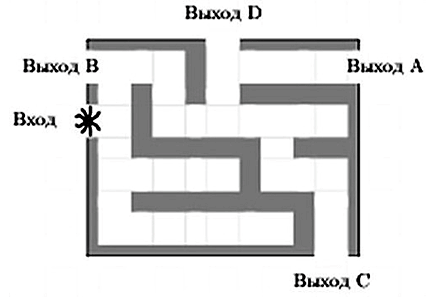 Решение: На каждой из встречаемых развилок у паука 2 варианта выбрать поворот, всего поворотов до выхода D надо преодолеть 4, значит, вероятность того, что он выйдет, именно, через этот выход равна 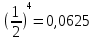 Ответ:  21 (320187). При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,8? Решение: Пусть событие А – цель уничтожена, p(А)>=0,8 C 1 выстрела: 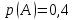 Cо 2 выстрела: 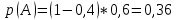 C 3 выстрела: 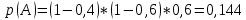 … 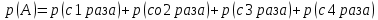 0,4 0,36 0,144 0,76<0,8 0,904>=0,8 Нужно всего три выстрела Ответ: 3 выстрела. 22 (320206). В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. Решение: Возможны следующие случаи:
Ответ: 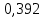 23 (320188).Чтобы пройти в следующий круг соревнований, Футбольной команде нужно набрать хотя бы 5 очков в двух играх. Если команда выигрывает, то она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятность выигрыша и проигрыша одинаковы и равны 0,4. Решение: Р(Н) = 1 – Р(В) – Р (П) = 1 – 0,4 – 0,4 = 0,2 Всего исходов – 9 (ВВ, ВП, ВН,ПВ,ПП,ПН,НВ,НП,НН). Так как команде нужно набрать 4 очка, то благоприятных исходов – 3 (ВВ, ВН, НВ). Р(ВВ) = 0,4 *0,4 = 0,16; Р (ВН) = Р(НВ) = 0,4*0,2 = 0,08. Р(выйти в следующий круг) = 0,16 + 0,08 + 0,08 = 0,32. Ответ: 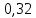 24 (320200). На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых. Решение: Пусть х – тарелок выпустили, тогда 0,1x c дефектом, 0,9х без дефекта. Тарелок, которые не поступят в продажу 0,8*0,1х=0,08х, поступят – 0,92х тарелок, но среди них с дефектами 0,1х-0,08х=0,02х тарелок. Итого тарелок в продаже 0,92х, без дефектов – 0,92х-0,02х=0,90х. Р=0,90х/0,92х=0,98 Ответ: 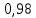 Заключение При написании данной творческой работы мы изучили большое количество дополнительной научной литературы по теме «Вероятность», расширили и углубили свои знания по данному вопросу, овладели простейшими и более сложными задачами с использованием теории вероятности. В ходе выполнения работы нами рассмотрены различные способы решения задач на применение теории вероятности. При решении задач оказалось, что их можно классифицировать по типам: Простые задачи а) о выборе объектов набора; б) задачи о подбросе монеты; в) задачи о кубике г) задачи о частоте Задачи повышенной сложности а) задачи на сумму несовместных событий; б) задачи на произведение независимых событий; в) сложение и умножение вероятностей Сложные задачи а) задачи о зависимых событиях; б) задачи на проценты; в) разные задачи Данный проект может быть использован учащимися 9-11 классов при самостоятельной подготовке к ОГЭ и ЕГЭ, а учителями математики как учебное пособие. Литература 1. Тюрин Ю.Н. Теория вероятностей и статистика / Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко. М.: МЦНМО: АО «московские учебники», 2004. 2. В.А. Булычев, Е.А. Бунимович «Комбинаторика. Элементы теории вероятностей и статистики». Журнал «Математика в школе»№5,№ 6,№ 7, 2011г 3. Г.И. Фалин «Преподавание теории вероятности в школе». Журнал «Математика в школе»№2, №3, №4 2014г 4. И.В. Ященко, С.А. Шестаков Математика ОГЭ 2019, Из-во «Просвещение» 5. Открытый банк заданий по математике http://prof.mathege.ru/prototypes/?position=5 6. Открытый банк заданий по математике https://math-oge.sdamgia.ru/?redir=1 |
