Родионова Наталья Евгеньевна Донской, 2019 Содержание Введение в 2003 году было принято решение
 Скачать 95.59 Kb. Скачать 95.59 Kb.
|
|
Глава 2. Практическая часть 2.1 Задачи ОГЭ В кармане у Пети было пять конфет – «Ласточка», «Буревестник», «Взлётная», «Василёк» и «Грильяж», а также проездной. Вынимая проездной, Петя случайно выронил из кармана одну конфету. Найдите вероятность того, что выпала конфета «Василёк». Решение: Благоприятствует падению конфеты «Василёк» только одно элементарное событие, всего же их 5 (по одному на каждую конфету), получаем 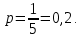 Ответ: 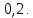 Коля, Костя, Паша, Маша и Таня бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру будет мальчик. Решение: Пусть событие А – игру начинает мальчик. Всего пять детей, из них трое мальчики, следовательно, 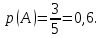 Ответ: 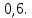 Родительский комитет закупил 20 пазлов для подарков детям, из них 10 с машинами и 10 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Антон. Найдите вероятность того, что Антону достанется пазл с машиной. Решение: Число детей совпадает с количеством подарков. Значит, все подарки будут розданы и каждому ребёнку достанется пазл, следовательно, 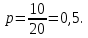 Ответ: 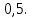 В группе туристов 10 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин. Решение: Выбрать пару человек можно 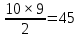 , из них турист Д. входит в 9, то есть , из них турист Д. входит в 9, то есть 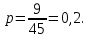 Ответ: 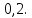 Конкурс проводится 4 дня. Всего заявлено 60 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. Все выступления поровну распределены между конкурсными днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность того, что выступление исполнителя их России состоится во второй день конкурса? Решение: Всего из 60 выступлений на второй день запланировано 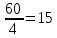 , отсюда, , отсюда, 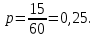 Ответ: 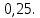 В ящике находятся белые и чёрные шары, причём чёрных в 3 раза больше, чем белых. Из ящика случайным образом, не глядя, достали один шар. Найдите вероятность того, что он будет белым. Решение: Пусть белых шаров x, тогда чёрных 3x, а всего шаров 4x, тогда 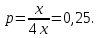 Ответ: 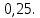 При подведении итогов ОГЭ среди девятиклассников города обнаружилось, что экзамен по русскому языку не сдали 4% участников, а среди них 23% участников не сдали экзамен по математике. Среди тех, кто сдал русский язык, 97% участников сдали математику. Найдите вероятность того, что случайно выбранный в этом городе девятиклассник сдал экзамен по математике. Решение: Вероятность не сдачи русского языка равна 0,04, при условии происхождения этого события математика сдаётся с вероятностью 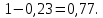 Сдаётся русский с вероятность Сдаётся русский с вероятность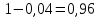 , при этом математика с 0,97. Тогда по формуле полной вероятности , при этом математика с 0,97. Тогда по формуле полной вероятности 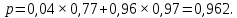 Ответ: 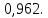 На птицеферме разводят кур, уток и гусей. Известно, что гусей на 40% меньше, чем уток, а кур на 140% больше, чем уток. Найдите вероятность того, что случайно увиденная на этой птицеферме птица окажется гусём. Решение: Пусть x – количество уток, тогда 2,4x – кур, 0,6x – гусей, то есть всего птиц 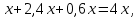 тогда вероятность встретить гуся равна тогда вероятность встретить гуся равна 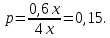 Ответ: 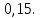 Из крупных животных в заповеднике обитают косули, олени и лоси. Найдите вероятность того, что случайно увиденное в заповеднике крупное животное окажется косулей, если из трёх следующих утверждений два истинны, а одно ложно: лоси составляют 34% крупных животных заповедника; олени составляют 45% крупных животных заповедника; косули составляют 67% крупных животных заповедника; Решение: Третье утверждение ложно, так как в противном случае, какое бы из других двух утверждений не было бы верно, то получается, что два вида крупных животных в сумме составляют более 100%, а значит верны первые 2 утверждения, то есть 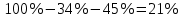 составляют косули, тогда вероятность встретить косулю равна составляют косули, тогда вероятность встретить косулю равна 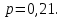 Ответ: 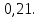 В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что оба автомата неисправны. Решение: Так как вероятность неисправности каждого автомата равна 0,1 и эти события независимы, то 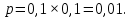 Ответ: 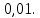 2.2 Задачи ЕГЭ 1 (320184). Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию 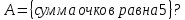 Решение: На кубике могут выпадать числа от 1 до 6. Составим таблицу исходов для суммы очков двух бросков кубика
Ответ: 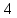 2 (282858). В соревнованиях по толканию ядра участвуют спортсмены из четырёх стран: 4 из Финляндии, 7 из Дании, 9 из Швеции и 5 из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Швеции. Решение: Пусть событие A – первым выступает спортсмен из Швеции. Всего спортсменов со всех стран 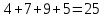 . Значит, искомая вероятность равна: . Значит, искомая вероятность равна: 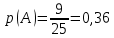 Ответ: 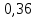 3 (320191). На олимпиаде по русскому языку 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 120 человек, оставшихся перевели в запасную аудиторию в другом корпусе. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. Решение: Пусть событие R заключается в размещении студента в запасной аудитории. Всего олимпиадников попадает в эту аудиторию 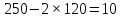 человек. Отсюда, вероятность попадания в другой корпус равна: человек. Отсюда, вероятность попадания в другой корпус равна: 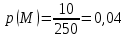 Ответ: 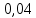 4 (285922). Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые 3 дня по 17 докладов, остальные распределены поровну на последние два дня. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на пятый день конференции. Решение: Пусть событие M – профессор М. выступает с докладом в последний день конференции. На этот день запланировано 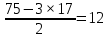 докладов. Отсюда, требуемая вероятность равна: докладов. Отсюда, требуемая вероятность равна: 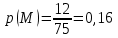 Ответ: 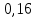 5 (285925). Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 спортсменов из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России. Решение: Пусть событие R – в пару с Русланом попал другой спортсмен из России. Всего пар, включающих Орлова, 25, а со спортсменами из нужной страны 9, тогда вероятность равна: 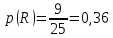 Ответ: 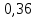 6 (325904). За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом. Решение: Допустим, что мы посадили одну из девочек за стол. Пусть событие N – вторая девочка сядет рядом, для нее может быть 2 благоприятных исхода. Еще есть 9-1-2=6 мест. Всего свободных мест 6+2=8 мест. 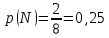 . .Ответ: 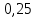 7 (320209). Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1. Решение: Так как стрелка достигла 10, но не дошла до 1, то она в сегменте, в который входят 3 отметки: 10, 11, 12. Так как всего отметок 12, то требуемая вероятность равна 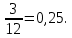 Ответ: 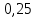 8 (508200). Фабрика выпускает сумки. В среднем на 92 качественных сумки приходится 8 сумок, имеющих скрытые дефекты. Найдите вероятность того, что выбранная в магазине сумка окажется с дефектами. Решение: Так как в среднем на 92 качественные сумки приходится 8 сумок, имеющих скрытые дефекты, то в среднем из 100 сумок 8 с дефектами, то есть нужная вероятность равна  Ответ: 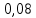 9 (320196). При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 66,99 мм, или больше чем 67,01 мм. Решение: Пусть событие D – отличие диаметра от стандарта больше, чем на 0,01 мм. Очевидно, что оно совпадает с событием «диаметр меньше, чем 66,99 мм, или больше, чем 67,01 мм» и противоположно событию «диаметр будет отличаться от заданного не больше, чем на 0,01 мм». Из противоположности событий имеем: 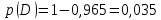 Ответ: 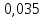 10 (319355). Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: Пусть событие W заключается в победе А., при игре белыми, а событие B – в его выигрыше, при игре чёрными. Так как эти события не зависят друг от друга и он должен выиграть оба раза, то это одновременные события, то есть вероятность абсолютной победы А. равна 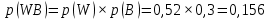 Ответ: 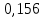 11 (282853). В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 8. Результат округлите до сотых. Решение: Пусть событие A – в сумме выпало 8 очков. Это могло случиться в случае выполнения одного из следующих несовместных событий: выпало 2 и 6, 3 и 5, 4 и 4, 5 и 3, 6 и 2 очков. Всего вариантов выпадения очков на двух костях 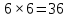 . Тогда по формуле полной вероятности, . Тогда по формуле полной вероятности, 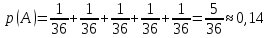 Ответ: 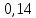 12 (320175). Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. Решение: Пусть событие G заключается в том, что лампочка не перегорит. Так как две лампочки не зависят друг от друга, то вероятность того, что одна из них не перегорит (событие L) равна 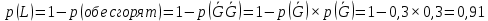 Ответ: 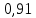 13 (320171). На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что этот вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что этот вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. Решение: Пусть событие O состоит в том, что достанется вопрос по окружности, а событие P – достанется вопрос по параллелограмму. Так как эти события несовместные, то вероятность появления одного из них (событие Q) равна 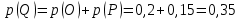 Ответ: 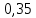 14 (320173). Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишень, а последние два промахнулся. Результат округлите до сотых. Решение: Пусть события 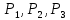 - попадания спортсмена в цель в первый, второй и третий разы соответственно, а - попадания спортсмена в цель в первый, второй и третий разы соответственно, а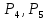 – промахи на четвертый и пятый выстрелы. Так как эти события не зависят друг от друга, а вероятность промаха равна – промахи на четвертый и пятый выстрелы. Так как эти события не зависят друг от друга, а вероятность промаха равна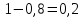 , то вероятность их одновременного появления равна , то вероятность их одновременного появления равна 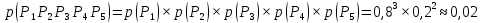 Ответ: 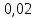 |
