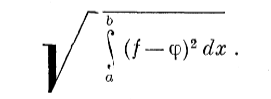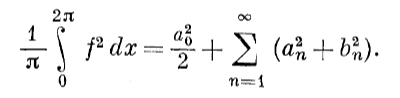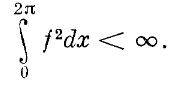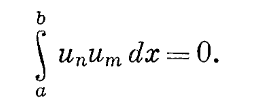математика. Рождение и первые шаги Московской
 Скачать 180.54 Kb. Скачать 180.54 Kb.
|
1 2 0Образовательное учреждение Среднего профессионального образования Медицинский колледж «Авиценна Билим» РЕФЕРАТ На тему: Рождение и первые шаги Московской школы теории функций действительного переменного. Выполнил(а): Авулова Мехрибону Группа: Стоматология Проверил(а): Бишкек, 2022 МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ЮКОЛЫ Л. А. Л ю к с т е р н и к В 61-м году я по состоянию здоровья был некоторое время оторван от обычной работы. Тогда я написал (сначала мысленно) свои воспоминания. которые озаглавил «Молодость Московской математической школы», отно- сящиеся к началу двадцатых годов — «периоду Л узитании» и отчасти к их середине, что названо здесь условно «периодом Постлузитании» '). Когда говорят о математике рассматриваемого периода, то под «Московской мате- матической школой» понимают часто не всю московскую математику, а то , что следовало бы назвать Московской теоретико—множественной школой, — школу теории функций и отпочковавшиеся от неe школы в направления. Эта Московская школа в узком смысле переживала тогда cвoю молодость, и это совпадало с физической молодостью большинства входивших в нее математиков. Быстрый рост этой школы, явившейся основной базой раз- вития московской математике, начался в трудных условиях начала 20-х годов. Он привел к тому, что Москва к их концу стала впервые крупнейшим в международном масштабе математическим центром. Это была несомненно яркая страница в истории советской культуры. Итоги научной работы этого периода подведены под свежим впечатлением — в юбилейных сборниках к Х-летию и ХV-летию ревоюлции, в ретроспективно — в позднейших сборниках . Но поскольку осталось не так уже много тех, кто непосред ственно «изнутри» наблюдал этот процесс раннего развития Московской математической школы, я позволил себе опубликовать этот материал. Всякое воспоминание поневоле субъективно — не все видишь, не все припоминаешь, и людей иногда видишь со стороны не наиболее характерной и интересной. Далее мы знаем последующие судьбы людей и их взаимоотношений, судьбы научных школ и направлений, мероприятий и т. д., и трудно бывает отвлечься от этой апостериорной информации. В картинах китайских и японских мастеров часто отдельные фрагменты изображаются детально, остальное воспринимается как фон. Так и память, отдельные эпизоды, иногда второ степенные, воспроизводит ярко, остальное — в виде «фона». Мы не придерживались хронологического порядка. Иногда делали экскурсии вперед по времени, иногда назад. Одна большая экскурсия назад Фрагмент из этих воспоминании был опубликован в УМН XX, вып. 3 (1965), 2 1 - 3 0 . Л. А. ЛЮСТЕРНИК превратилась в приводимый сейчас очерк «Страницы из истории матема тики», выпадающий из рамок воспоминаний. Мы позволили себе включить его в качестве историко-математического введения к ним. Добавим, что личные воспоминания автора дополняются иногда рас сказами других лиц. 1. Страницы из истории математики 1. Тригонометрические ряды и основные понятия анализа. Это исто рическое отступление должно рассказать о том, как сложилась «математи ческая ситуация» второго десятилетия XX века, когда начала формироваться Московская теоретико-множественная школа. «Необъятного никто объять не может». Поэтому мне придется ограничиться односторонним описанием, взглянув на прошлое глазами математика двадцатых годов, который видел расцвет в Москве школы теории функций, рождение и развитие топологи ческой школы, первых ласточек школы функционального анализа, начала работы в более классических областях математики на базе этих, тогда еще молодых математических дисциплин. Иногда, заглядывая в прошлое, мы видели корни отдельных направлений сегодняшней работы более глубоко. Так, в теории тригонометрических рядов — любимой теме московских математиков в период формирования нашей школы — существовала со времен Римана традиция начинать изложение с задачи о звучащей струне. В большинстве случаев мы знали лишь своих более близких научных предков. Мы начнем поэтому изложение с нескольких страниц истории тригоно метрических рядов. В математике бывают задачи, приводившие к «возвращению к основам данной науки» (выражение Лобачевского), например, задача о доказатель стве V постулата в геометрии. В анализе неоднократно играла такую роль теория тригонометрических рядов (это еще соображение, чтобы начать именно с нее). Как известно, эта задача сыграла роль в оформлении сов ременного понятия функциональной зависимости, обобщении понятия инте грала, имела отношение к возникновению теории множеств (было бы инте ресно проследить с аналогичной точки зрения и некоторые другие задачи). Первым аналитическим аппаратом изображения функций были сте пенные ряды, и анализ вначале имел дело лишь с функциями, разлагае мыми в такие ряды (мы сейчас называем такие функции аналитическими). Они обладают рядом замечательных свойств: так, в классе аналитических функций функция, заданная на каком-нибудь интервале, однозначно опре деляется своими значениями на частичном интервале — это свойство одно значности продолжения Л. Эйлер иногда называл «непрерывностью». Те опе рации, с которыми имели дело тогда математики,— алгебраические, супер позиция и обращение, дифференцирование и интегрирование, решение обыкновенных дифференциальных уравнений — выполнялись в пределах этого класса функций. Положение изменилось, когда начала складываться «математическая «физика», стали изучаться процессы, выраженные уравнениями в частных 140 Л . А. Л Ю С Т Е Р Н И К Изображение коэффициентов ряда (4) через сумму этого ряда: 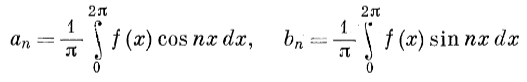 (5) было известно еще Эйлеру, но за выражаемыми по формуле (5) коэффициен тами осталось название «коэффициентов Фурье» для функции / (#), а за рядом (4) с такими коэффициентами —«ряда Фурье» этой функции. В работе Дирихле и Лобачевского по тригонометрическим рядам уже появилось современное понятие функции у = / (х) как произвольного соот ношения между значениями х и отвечающими им значениями у. При такой широкой точке зрения на понятие функции появилась задача найти по воз можности более широкие достаточные условия равенства функции / (х) сумме ее тригонометрического ряда Фурье. В 1829 г. появилось первое строго проведенное доказательство Дирихле справедливости такого равен ства при сравнительно широких достаточных условиях. Позже эти условия были расширены рядом авторов. Но если сумма / (х) ряда (4) может быть разрывной, то какой смысл нужно придавать интегралам в формулах (5), когда интеграл был определен лишь для непрерывных функций? Так возникла проблема «интеграла и три гонометрического ряда»— проблема «воссоздания коэффициентов ряда (4) по его сумме» (как ее определил Лузин). Она привела к созданию новых все более общих понятий интеграла, которые «действовали» во все более широких классах разрывных функций и придавали все более широкий смысл формулам (5) для коэффициентов Фурье. Эта проблема была фактически поставлена в классическом мемуаре Римана. Сейчас, когда отмечается столетие со дня кончины этого великого мате матика, уместно вспомнить следующее: Римана с его безудержным полетом математической фантазии часто противопоставляют Вейерштрассу с его критическим умом. Но гений Римана многогранен: в своем мемуаре по теории тригонометрических рядов (он был представлен в 1853 г. в геттингенский университет в качестве «Habilitationschrift»—«второй диссертации») Риман выступает в качестве одного из основоположников критического направления математики второй половины XIX века и предшественника теории функций действительного переменного. Мемуар начинается с истории вопроса о пред ставлении функций тригонометрическими рядами, начиная с 1753 г.,— с задачи о струне. Риман рассказывает со слов Дирихле такой, например, эпизод: когда Фурье в декабре 1806 г. рассказывал о своей теореме, то «это утверждение для маститого Лагранжа было столь неожиданным, что он выступил с самыми решительными возражениями». Рассказывая о том, что Дирихле различал «абсолютную» и «условную» (по позднейшей терминоло гии) сходимость, Риман попутно доказывает «теорему Римана» о влиянии перестановок членов на сумму ряда. Полагая, что «условию Дирихле» удовлетворяют все функции, могущие найти применение в физике, Риман считает «заслуживающими внимания всюду на периоде [0, 2л;], кроме конечного числа точек. Естественно возник вопрос: как обстоит дело, если / (х) = 0 всюду на [0, 2 я ] , кроме исключи тельного, но уже бесконечного множества точек К. Эта задача приводит к необходимости классифицировать такие множества, она и привела Г. Кан тора к созданию теории линейных точечных множеств (т. е. множеств веще ственных чисел). Согласно теперешней терминологии будем называть мно жество К точек (вещественных чисел) на отрезке [0, 2 я ] U-множеством (Unicite' — единственность) или множеством единственности, если не   Л. А. ЛЮСТЕРНИК •Не существует никакого тригонометрического ряда (1), кроме нуль-ряда, для которого его сумма / (х) = 0 всюду на [0, 2 я ] вне К; в противном случае назовем К М-множеством (множественности). Легко убедиться, что любой отрезок [а, Ь] — часть [0, 2 я ] есть М-множество. Кантор обна ружил существование и бесконечных [/-множеств. Это потребовало от него первых шагов в области теории точечных множеств. Свою работу 1872 г. «О тригонометрических рядах» Кантор начинает •с построения теории вещественных чисел («теория Кантора», основанная на фундаментальных последовательностях); далее он замечает, что уста новление взаимно однозначного соответствия между вещественными чис лами и точками прямой требует особой аксиомы (аксиома полноты). Рас сматривая множества вещественных чисел (точек), он вводит — на осно вании своего определения этих чисел — понятие предельной точки множе ства (точки сгущения); далее, понятие производной К' множества К — множества всех точек, предельных для К, и производных высших порядков: К" = (К')\ . . . , К&\ . . . , где К(р+1> = (КЮ)', причем при р > 1 , К(р+1) содержит КNo. Для конечного множества точек К предельных точек нет, К' = 0. Кантор исследует структуру множеств К, для которых К^ = 0, при любом конечном значении п и доказывает, что все они являются U-MHO- жествами. Именно этот мемуар 1872 г. по тригонометрическим рядам и был первым мемуаром Г. Кантора по теории точечных множеств, а она его привела к общей теории множеств. Уже в статье 1874 г. «Об одном свойстве понятия всех вещественных алгебраических чисел» Кантор доказывает теорему: для любой последовательности вещественных чисел можно строить веще ственное число, ей не принадлежащее. Располагая все вещественные алге браические числа в последовательность, он получает новое доказательство существования неалгебраических (трансцендентных) чисел. Это приводит к его классификации бесконечных точечных множеств по «мощностям» (1878 г.). Два множества называются эквивалентными, если между их элементами можно установить взаимно однозначное соответ ствие. Всем эквивалентным между собой множествам относится одна «мощ ность»— кардинальное число. Мощность конечного множества — это число его элементов. Далее все множества, эквивалентные множествам натураль ных чисел (1, 2, . . . , п, . . .) (а поэтому располагаемые в виде последо вательности) называются «счетными» и им всем приписывается общая мощ ность — счетная или алеф-нулъ». Примеры счетных множеств: множество всех рациональных чисел; всех алгебраических чисел; все ранее введенные множества К, для которых К^п) = 0. Но из вышеуказанной теоремы 1874 г. следует, что множество всех вещественных чисел есть несчетное. Его мощ ность Кантор называет «континуумом» или «алеф» (мощность С). Вопрос о том, существуют ли точечные множества других мощностей, составляет содержание континуум-проблемы Кантора. Мощность континуума имеет множество точек любого отрезка, любого «совершенного множества» Р на прямой (для которого Р' = Р). Эту же МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ШКОЛЫ мощность имеют и кубы n измерений и сами n-мерные координатные про- странства при любом числе п. Кантор далее обнаружил, что вышеуказанный процесс образований производных Р^ множества Р для любого конечного порядка п = 1, 2, 3, . . . можно продолжать «трансфинитно». Обозначим через Р^\ (производная порядка «со»— первого «трансфинитного» порядка) пересечение всех Р^п) для любых конечных п. Далее Р^+1) = (Р(м>)' и так строим />(«+2) , . . . . . ., Р(2со>, . . . Здесь Кантор впервые ввел трансфинитный процесс и отсю да пришел к теории трансфинитных порядковых чисел. Необычайным взлетом творческой математической фантазии Кантор в короткий срок (1874—1884 гг.) строит основы теории линейных точечных множеств и общей теории множеств. Творчество Кантора было «философским»: он вводил новые весьма общие понятия — такие, как «множество», «эквивалентность», «мощность», «порядок»,— эти понятия «работали». Но ему пришлось пережить драму новатора, не встречающего признания. Его учитель Л . Кронекер, стоящий на финитной точке зрения, пользовавшийся огромным авторитетом — не только в Германии, занял по отношению к теории Кантора резко отрица тельную позицию, и ее разделили многие тогдашние авторитетные мате матики, например, товарищ Г. Кантора Шварц. Не случайно в статьях Г. Кантора звучали патетические строки в защиту свободы математического творчества от метафизических предубеждений. «Смысл математики в ее свободе». В биографии Кантора (в собрании его сочинений) сказано, что он7 отстаивая свободу и независимость математического творчества и выступая против чрезмерного влияния отдельных ученых, явился одним из инициа торов создания математического общества Германии (Deutsche Mathematiker- vereinigung) и был его первым председателем. К счастью для науки, противники работ Кантора при всем их заслу женном авторитете и влиянии не обладали монополией: Кантор имел воз можность работать и публиковать свои труды. (Напомним, что, к счастью для науки, и противники Лобачевского при всем их авторитете и влиянии не обладали монополией: он имел независимую от них базу в Казани.) Напряженная работа в условиях борьбы за признание, возможно, содействовала тому приступу психического заболевания, которое впервые постигло Кантора в 1884 г., от которого он тогда вскоре оправился, но уже с ослабленной работоспособностью. Между тем наступала пора признания. С самого начала теорию Кантора поддерживал Дедекинд, самостоятельно пришедший к некоторым идеям тео рии множеств. Вейерштрасс, сначала встретивший ее отрицательно, изменил свое отношение (как позже и Эрмит под влиянием своего ученика А. Пуан каре). Внешним выражением признания заслуг Кантора было его избрание почетным членом Лондонского и Харьковского математических обществ (в 1901 г.), а затем и других научных организаций. Идеи Кантора приняли на вооружение такие крупнейшие математики следующих поколений, как А. Пуанкаре, Д. Гильберт, Г. Минковский, Ж . Адамар, А. Лебег и др. Успехи ма тем. на ук , т . XX I I , вып. 1 Л. А. ЛЮСТЕРНИК Начинается быстрое проникновение теории множеств во все области математики, на ее базе возникают новые математические дисциплины — теория функций действительного переменного, топология, функциональный анализ, математическая логика, общая алгебра и т. д. В 1915 г. предполагалось организовать международное чествование 70-летия Г. Кантора. Этому помешала война. Он умер в 1919 г. в психиа трической больнице. 3. Возникновение и развитие теории функций. Возвращение к основам анализа во второй половине X I X в., о котором мы говорили, выяснило, в частности, объем основных понятий анализа. Он оказался шире, чем объем связываемых с ними «наглядных представлений». Наглядные представле ния, например, о сходящейся последовательности функций отвечают не логически простому понятию сходимости в каждой точке, а более узкому — равномерной сходимости. Понятие непрерывной функции возникло, быть может, как модель механических процессов, и требование однозначной продолжаемости отра жало их детерминистический характер. Но и более широкий класс «произ вольно нарисованных линий» тоже содержит элемент движения, и ему, должно быть, соответствовал класс кусочно-гладких функций. Логически же простое определение Коши непрерывной функции оказалось значительно шире, чем связываемые с ней в то время наглядные представления; это и выяснил пример Вейерштрасса нигде не дифференцируемой непрерывной функции. (Впоследствии у Винера такие функции стали моделью более сложных процессов типа броуновского движения.) «Анализ основных поня тий анализа» сопровождался поэтому построением «парадоксальных» с пер вого взгляда примеров того, что называли «музеем математических ужасов». Противоречие между широтой объема логически простых понятий анализа и относительной узостью моделируемых ими наглядных представлений есть источник общеизвестных трудностей при прохождении курса анализа. Но именно эта широта определила возможность перенести такие понятия на более широкие объекты, чем «обычные» функции числового аргумента (см. ниже). Во второй половине X I X в. начала складываться новая дисциплина — теория функций действительного переменного, изучавшая общие понятия анализа — предельный переход, непрерывность, операции дифференциро вания и интегрирования; важнейшие аналитические выражения — как тригонометрические и ортогональные ряды, системы многочленов — и клас сы функций, ими изображаемые. Так теоремы Вейерштрасса выяснили, что класс непрерывных функций совпадает с классом изображаемых равно мерно сходящимися последовательностями многочленов. Конечно, теория функций формировалась на базе не только тригоно метрических рядов, но всех разделов анализа. В качестве примера приведу круг вопросов, связанных с «принципом Дирихле» (по терминологии Римана) — постулирования существования гармонической в области Q функции, с заданными значениями на границе. МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ШКОЛЫ как функции, реализирующей минимум функционала + ul) dxdy при заданных условиях1 ). Такое постулирование встречается у Гаусса в работах по теории потенциала, В. Томсона, Дирихле. Риман при доказательстве основных теорем теории аналитических функций пользуется «принципом Дирихле» и его аналогами, но в отличие от предшественников приводит соображения для оправдания такого принципа. В 1863 г. Вейер- штрасс критикует постулирование существования минимума вариационных задач, приводя пример задачи, для которой минимум не достигался. По словам Клейна, Риман, признавая правоту критики Вейерштрасса, про должал верить в правильность «принципа Дирихле». Критика Вейерштрасса направила Шварца и Неймана на успешные поиски невариационного обосно вания теорем Римана. Вейерштрасс в введении к своему курсу вариацион ного исчисления указал на недопустимость некритического постулирования существования минимума и для функций конечного числа переменных — на таком постулировании основано одно из доказательств V постулата Евклида. Вейерштрасс доказывает существование минимума непрерывной функции на отрезке — оно опирается на то свойство отрезка, которое мы нарываем компактностью — возможность выбрать сходящуюся последова тельность из всякой последовательности точек отрезка (для всей прямой не имеет места свойство компактности и минимум непрерывной функции на ней может не достигаться). В 1897 г. появилась работа Арцела о «принципе выбора» для непрерыв ных функций (условиях компактности систем таких функций в смысле равномерной сходимости). Это было связано с его попыткой обосновать принцип Дирихле. Наконец, в 1901 г. Гильберт доказал существование решений целого класса вариационных задач, опираясь на свойства компакт ности «минимизирующих последовательностей для них». Он дал вариацион ное обоснование и принципа Дирихле и теорем Римана, открыв широкую дорогу вариационным методам теории дифференциальных уравнений. Понятие компактности стало одним из основных в теории функций, топологии, а после работ Гильберта по теории линейных операторов — и в функциональном диализе. Другой пример — появление в работах Стилтьеса по «проблеме момен тов» в 1895 г. названного его именем интеграла. Интеграл Стилтьеса — обобщение интеграла Римана — объемлет и алгебраическую операцию конечного суммирования и предельные для нее операции анализа — обычное- интегрирование, суммирование рядов и т. п. Стилтьес переходил к пределу в названной работе от алгебраической задачи к задаче анализа; интеграл Стилтьеса оказался аппаратом, удобным для такого предельного перехода. Мы уже видели, что задачи теории функций привели Кантора к созда нию теории множеств, а последняя нашла (еще у Кантора) свои первые при ложения именно к теории функций. !) С. С. П е т р о в а , О прирщипе Дирихле, История и методология естествен ных наук 5 (1966). 10* Л. А. ЛЮСТЕРНИК Теория функций действительного переменного (к которой относят и теорию линейных точечных множеств) получила свое окончательное оформление в начале XX века в ставших классическими трудах француз ских математиков — Анри Лебега, Рене Бэра, Эмиля Бореля. В теории линейных точечных множеств после работ Кантора крупным событием было введение в 1902 г. меры Лебега точечного множества, обобщаю щей понятие длины отрезка (заметим, что в числе предшествовавших меро определений было и мероопределение Кантора, данное сразу для ^-мер ного случая). Преимуществом мероопределения Лебега явилась его общность — ни одна конструкция не приводила к неизмеримому по Лебегу множеству; с другой стороны,— его логическая простота. Аксиоматика меры Лебега чрезвычайно проста. Это позволило впоследствии ее обобщить на множества самой разнообразной природы. Среди измеримых точечных множеств особо выделим множества меры 0 — все конечные и счетные, а также некоторые контитуальные (примером его служит множество тех вещественных чисел, в десятичном представлении которых ни разу не появляется какая-нибудь цифра, например, 8). При интеграции можно пренебречь значениями функций на множестве меры 0. Если свойство А имеет место для всех точек, кроме принадлежащих множе ству меры 0, мы говорим: оно имеет место почти всюду. Например, пусть ап (х) — число появлений цифры 7 среди первых п цифр десятичного раз ложения числа х. Имеем: почти всюду 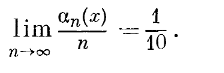 Мы называем метрической теорией функции ту ее часть, которая свя зана с понятием меры,— сюда относится теория интегрирования, сходимости почти всюду и других свойств «почти всюду», сходимости в среднем и т. п. Каждая функция / (х) преобразует множества на оси х в множества оси у. Функция f (x) называется измеримой по Лебегу, если прообраз любого отрезка [а, Ь] оси, т. е. множество точек х, для которых a^f(x)^b, измерим. Здесь мы встречаемся с соответствием между классами функций / (х) и классами точечных множеств. Классу К таких множеств отвечает класс К тех функций / (х), для которых прообразы отрезков оси у суть множества класса К оси х. Одновременно с мероопределениями Лебега появился и интеграл Лебега, более общий, чем интеграл Римана. Грубо говоря, если с интегралом Римана мы связываем разбиения отрезка интегрирования на интервалы, то для интеграла Лебега мы аналогично используем его разбиения на про извольные измеримые множества. Аксиоматика интеграла Лебега также весьма проста, проще аксиоматики интеграла Римана; эта логическая простота позволила перенести позже на функции, определенные на множе стве общей природы, понятие интеграла Лебега. Интеграл Лебега и его дальнейшее обобщение — интеграл Дан- жуа — возникли в теории тригонометрических рядов в связи, как уже указывалось, с задачей придать более широкий смысл коэффициентам МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ШКОЛЫ Фурье. В этой теории и получила свои первые применения метрическая теория функций. Проиллюстрируем это двумя примерами. Теорема Парсеваля — Ляпунова легко обобщается на измеримые функ ции с интегрируемыми по Лебегу квадратами (их мы будем иметь в виду, говоря о функциях с интегрируемыми квадратами). В 1910 г. была доказана в известном смысле обратная ей теорема Фишера — Рисса. Если у тригоно- оо метрического ряда (4) 7 1 = 1 с интегрируемыми квадратами / (х), для которой он будет рядом Фурье (и поэтому имеет место равенство Парсеваля (6)). Теоремы Парсеваля — Ляпунова и Фишера — Рисса полностью решают вопрос о представлении функций тригонометрическими рядами в смысле сходимости в среднем. Теорема Фишера — Рисса распространяется на любые ортогональные системы. В качестве второго примера приведем классическую задачу Кантора о единственности разложений в тригонометрические ряды. Кантор показал, что конечные множества и некоторые счетные являются множествами един ственности ([/-множествами). С другой стороны, легко показать, что множе ства положительной меры — имеющие мощность континиум — являются М-множествами. В 1907 г. Юнг доказал, что все счетные множества являются [/-множествами. Одно время предполагалось, что только счетные множества являются [/-множествами. Поэтому сенсационным было в 1914 г. построение московским математиком Д. Е. Меньшовым примера совершенного множества меры 0 (имеющего континуальную мощность) и являющуюся U-множеством. А позднее Н. К. Бари построила пример совершенного множества меры 0, являющегося М-множеством, причем оказалось, что именно арифметические свойства множеств меры 0 определяют, являются ли они U- или М-множе ствами. Наряду с метрической возникла и «дескриптивная» теория функций, не связанная с понятием меры. Она рассматривает, например, сходимость функции всюду. Р. Бэр нашел необходимые и достаточные условия для того, чтобы разрывная функция была пределом непрерывных', такая функция назы вается функцией 1-го класса (непрерывные функции будем считать функ циями нулевого класса). Вообще функцией п-го класса будем называть предел функций классов, меньших п, которые сами этим классам не принадлежат. Эта классификация распространяется не только на классы конечного, но и трансфинитного порядка и их объединение есть множество функций, получаемых счетно-кратным переходом к пределу, исходя от непрерывных. Это объединение называется «борелевским телом» функций — наименьшее множество функций, инвариантное по отношению к операции предельного перехода. Все функции этих классов называются 5-функциями. Им, согласно описанному принципу соответствия, отвечают Б-множества. Долгое время считалось, что любые операции анализа не выводят за пределы классов 2?-функций и 5-множеств. В теории функций действительного переменного получили развитие те методы анализа, которые можно назвать «конструктивными». Понятие Л. А. ЛЮСТЕРНИК меры, например, исходит из меры отрезка, распространяет его на другие элементарные объекты, получаемые из отрезков их суммированием и вычи танием. Наложение предельного перехода на эти элементарные конструкции приводит к понятию меры для очень общих и сложных множеств. Для теории функций характерно сочетание элементарных конструкций с услож няющим предельным переходом. Теория функций и ее методы широко про никли во все разделы анализа. В первом десятилетии XX века оформилось еще одно направление теории функций —«теория приближений» или по терминологии С. Н. Бернштейна — «конструктивная теория функций» (конструктивная — в смысле алгорит мическая, не в указанном выше смысле). Как известно, П. Л . Чебышёв был создателем теории многочленов наилучшего приближения. «Уклоне нием» функций / (х) и ф (х) на [а, Ъ] он называл max | / (х) — ф (х) | (то, что теперь называют метрикой С), многочленом наилучшего приближения степени п — тот из многочленов степени п, чье уклонение от данной функции наименьшее). В 1885 г. Вейерштрасс доказал теорему о том, что всякая непрерывная на [а, Ь] функция есть предел сходящихся к ней равномерно многочленов. Эти работы были исходными для теории приближений, осново положниками которой были в первую очередь С. Н. Бернштейн, а также Валле-Пуссен, Джексон и др. Классифицируя непрерывные функции по скорости сходимости к ним многочленов наилучшего приближения, С. Н. Бернштейн выделил, в част ности, класс аналитических функций вещественного переменного, а также более общие классы «квазианалитических функций», в пределах которых сохраняется однозначность продолжения. Другие классы квазианалитиче ских функций были построены Карлеманом и Данжуа. Так в современном анализе нашла свое место «непрерывность» математиков XVIII века в смысле однозначной продолжаемости. 4. Теоретико-множественная концепция. Мы остановились подробнее на теории функций действительного переменного потому, что с нее нача лось формирование Московской математической школы. Одновременно с ней развиваются другие новые направления математической работы, опирающиеся на теории множеств. В первые десятилетия XX века во всей математике восторжествовала теоретико-множественная точка зрения, рассматривавшая как объекты различных разделов математики классы множеств, между элементами кото рых установлены того или иного рода соотношения. В геометрии эта точка зрения была подготовлена ее эволюцией в X I X веке — созданием неевкли довых геометрий и других геометрических систем, тг-мерных геометрий и т. д. Теоретико-множественная точка зрения рассматривает геометриче ские системы как множества объектов, между которыми установлены соот ношения, обобщающие соотношения обычного пространства. Основные соот ношения образуют аксиоматику данного класса геометрических объектов — «пространств».  МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ШКОЛЫ МОЛОДОСТЬ МОСКОВСКОЙ МАТЕМАТИЧЕСКОЙ ШКОЛЫАналогично в алгебре теоретико-множественная точка зрения была подготовлена обобщением понятия числа, созданием таких алгебраических объектов, как группы, кольца, поля, линейные системы и т. д., над эле ментами которых производятся операции, в каком-то смысле обобщающие алгебраические операции над числами. Теоретико-множественная точка зрения в алгебре рассматривает эти объекты как множества, над элементами которых производятся операции, сохраняющие некоторые свойства алге браических операций над числами; основные свойства этих операций уста навливают аксиомы соответственных классов объектов. Теоретико-множе ственная точка зрения привела к универсализации аксиоматического метода. С расширением математического материала объединяющие концепции строились на все более высоком уровне абстракции. Для математики конца XIX и начала XX веков этим уровнем был «уровень теории множеств». На базе теории множеств происходило переосмысливание отдельных математических дисциплин, обобщение их основных понятий. Это обобщение расширило возможность их применения; методы и понятия одних математи ческих дисциплин стали переноситься в другие. Так, понятие меры и интеграла Лебега были перенесены в теорию топо логических групп, в теорию вероятностей и другие математические дис циплины. Это было бы сделать гораздо трудней на уровне интеграла, напри мер, Римана и более узких понятий меры1 ). Обобщение основных понятий алгебры и геометрии привело к широкому проникновению их методов в разные области математики. Так в математике XX века наряду с тенденциями к дифференциации проявились и синтетические тенденции. Поучительной является история московской теоретико-множественной математической школы. Возникнув в 10-х годах как школа теории функций действительного переменного, она довольно быстро «овладела» методами работы в самых различных областях математики. При этом целый ряд своих достижений она имела на стыке разных математических дисциплин. Заметим в заключение, что теория множеств возникла в связи с воз вращением к основам анализа, что ее концепции проникли в другие науки в связи с возвращением к их основам, и вместе с тем она поставила задачу возвращения к собственным основам. Уже вскоре после появления основополагающих работ Кантора выяви лись «антиномии теории множеств». Их анализ показал, что требуется осторожность при перенесении рассуждений, законных для конечных множеств, на бесконечные. С другой стороны, трудности, возникшие при доказательстве континуум-проблемы и других родственных задач, потре бовали критического пересмотра самого понятия «доказать». В десятых годах среди работников теории функций и теории множеств возникли споры о законности применения некоторых видов доказательства для бесконечных г) Заметим, что уже переход от одномерного интеграла к кратным на уровне инте грала Лебега проще, чем на уровне интеграла Римана (недавно Г. Е. Шилов в читаемом им курсе анализа в МГУ произвел в этом направлении удачный эксперимент построения такого курса). Л. А. ЛЮСТЕРНИК множеств. Наконец, развитие аксиоматического метода поставило задачу аксиоматизаций теории множеств. Возникшие таким образом вопросы осно вания теории множеств оказались вопросами наиболее глубоких оснований математики в целом, это стимулировало развитие математической логики. Д. Гильберт, чьи исследования по основаниям геометрии явились образцом аксиоматического исследования, впоследствии явился основоположником «теории доказательств». 5. Некоторые новые направления математической работы. Указанные тенденции — к обобщению основных понятий, возникновению новых более общих направлений математической работы, к созданию синтетических концепций — мы проиллюстрируем на нескольких примерах из области геометрии и анализа. Обобщение основных геометрических понятий завер шилось созданием абстрактных пространстве, аксиоматика которых сохра няет лишь минимальное число наиболее общих свойств обычных пространств. Первым было появление в 1904 г. метрических пространств (М. Фреше). Это множества, для каждой пары а и b элементов («точек») в которых уста новлено понятие «расстояния» — числа р (а, Ь), удовлетворяющего трем аксиомам: 1) р (а, 6 ) > 0 , причем] р (а, б) = 0 тогда и только тогда, когда а = Ь; 2) р (а, б) = р (Ь, а); 3) р (а, с ) < р (a, b) -f p (Ь, с) (аксиома тре угольника). В метрических пространствах установлен закон предельного перехода (именно lim ап = а означает: lim р (а, ап) = 0). Позже (у П-*оо ft->oo Ф. Рисса, 1909 г.) появляются более общие «топологические» пространства, у которых установлена лишь «топология», т. е. законы предельного перехода. Абстрактные пространства охватили как все ранее появляющиеся «классические» геометрические системы, так и «функциональные простран ства», элементами которых являются функции, кривые, последовательности. Чебышёв, исследуя приближения функций многочленами и другими элементарными функциями, вводил разные числовые характеристики бли зости функций / (х) и ф (х) на [а, Ь]: уклонение (см. выше); среднеквадра- тическое — с весом величине, т. е. | / — ‹р | d:r.Все эти характеристики могут рассматриваться как расстояния между функциями (по современной терминологии Чебышёв пользовался метриками С, L2ф, L). Множества функций с такой метрикой образуют основные функциональные пространства. Расширение объектов геометрических исследований выразилось также в том, что и в пределах более обычных пространств стали рассматриваться не только «классические образы»— многогранники, «гладкие» линии, поверх ности, многообразия, но и более общие множества точек. Наряду с классическими преобразованиями точечных множеств по явились и более общие. Как показал Г. Кантор, произвольные взаимно одно значные преобразования «разрушают» такие основные свойства геометриче ских объектов, как число измерений.  1 2 |