Курс лекций по основам. Роль с Х. науки в развитии апк страны
 Скачать 1.33 Mb.
|
|
Дисперсионный анализ с расчётом отклонений от среднего урожая по опыту  о (модель I-я)Расчёты проводят в несколько этапов: 1- й этап: Составляют таблицу урожаев, подсчитывают суммы по вариантам V, повторениям Р и общую сумму всех поделяночных урожаев ∑Х. При правильных вычислениях сумма всех сумм по вариантам ∑V и сумма всех сумм по повторениям ∑Р должны быть равны между собой и общей сумме поделяночных урожаев ∑Х, т.е. ∑V=∑Р=∑Х. Вычисляют средние по вариантам  =  по повторениям р = и средний урожай по опыту о =  Поделяночная урожайность пшеницы в опыте с изучением способов обработки почвы, ц/га
2-й этап:. Составляют вспомогательную расчётную таблицу отклонений поделяночных урожаев Х от среднего урожая по опыту о (Х-о), отклонений средних по вариантам от о ( - о) и средних по повторениям р от о (р-о). Находят суммы отклонений по вариантам ∑(-о), повторениям ∑(р-о) и общую сумму отклонений ∑(Х-о). При правильных вычислениях ∑(-о)= ∑(р-о)= ∑(Х-о). Затем все полученные отклонения возводят в квадрат, заносят в правую часть таблицы (таблицу квадратов отклонений) и подсчитывают суммы квадратов отклонений ∑(-о)2, ∑(р-о)2 и ∑(-о)2.Таблица отклонений и квадратов отклонений от о
3-й этап: Вычисляют суммы квадратов отклонений для разных видов варьирования. а) Общее варьирование Су характеризуется суммой квадратов отклонений поделяночных урожаев Х от среднего урожая по опыту о: б) Варьирование по повторениям  равно сумме квадратов отклонений средних урожаев по повторениям  р от среднего по опыту о, умноженной на число вариантов: в)Варьирование по вариантам  равно сумме квадратов отклонений средних урожаев по вариантам от среднего урожая по опыту о, умноженной на повторность в опыте: Случайное (остаточное) варьирование  определяется по разности   4-й этап: Определяют степень влияния каждого из факторов в отдельности на изучаемый признак (урожай), принимая общее варьирование (дисперсию) за 1 или 100%: влияние вариантов -  (75%);влияние повторений -  (12%);влияние случайных факторов -  (13%).Если на долю варьирования вариантов по сравнению с влиянием случайных ошибок приходится наибольший процент, как в данном примере, то расчёты нужно продолжить дальше и установить существенность влияния изучаемых факторов на урожай. Когда величина  < , это значит, варьирование урожаев по вариантам в основном обусловлено влиянием случайных факторов. В этом случае расчёты можно не продолжать.5-й этап: . Составляют таблицу дисперсионного анализа, в которую заносят значения различных видов варьирования, вычисляют степени свободы этих варьирований, дисперсию вариантов, дисперсию ошибок и отношение этих дисперсий, т.е. фактическое значение критерия Фишера Fфакт Число степеней свободы равно: Для общей дисперсии (варьирования) –  ;для дисперсии повторений –  ;для дисперсии вариантов –  ;для остаточной дисперсии –  .Таблица дисперсионного анализа
Не все средние квадраты (дисперсии) представляют интерес для оценки результатов опыта. Наиболее важными из них являются дисперсии вариантов  и ошибок  . Первая характеризует варьирование урожаев. Равенство их проверяется по критерию :дисперсия вариантов – =  ;дисперсия ошибок - =  ;значение критерия – 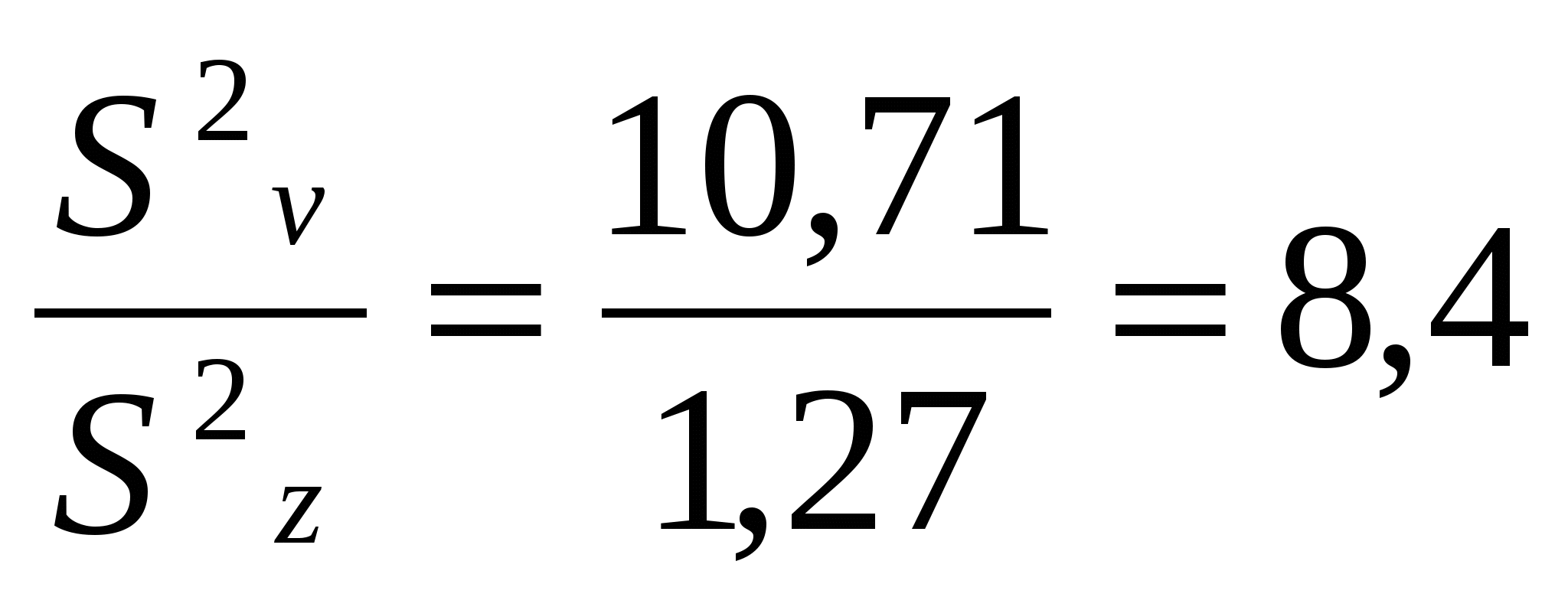=  .Теоретическое значение критерия для принятого уровня значимости (05 или 01) находят по прил. 3 и 4 при числе степеней свободы для дисперсии вариантов  и дисперсии ошибок  .Заключение по критерию Фишера ( F ) По критерию  устанавливают наличие в опыте вариантов, имеющих существенные разности урожаев. Наличие в опыте вариантов с существенной прибавкой или снижением урожая подтверждается, когда ≥  . Если < , то между средними по вариантам нет существенных различий, т.е. различия между вариантами находятся в пределах ошибки опыта или в опыте имеет место нулевая гипотеза – Но. В этом случае оценку частных различий (между средними по вариантам не проводят. При ≥ дают оценку существенности частных различий по критерию  .6-й этап: На этом этапе оценивают существенность разности (частных различий). Под частными различиями понимают разности между средними урожаями опытных вариантов и контролем, а также разности средних урожаев опытных вариантов между собой. Количество этих разностей находят: d = ℓ×(ℓ - 1) : 2 = 4×(4 – 1) : 2 = 6d1 = х2 – хк d2 = х3 – хк d3 = х4 – хк d4 = х3 – х2 Эти разности называются частными различиями d5 = х4 – х2 d6 = х4 – х3 Чтобы доказать существенность этих различий, рассчитывают ещё три вида показателей: 1. Ошибка опыта в абсолютных величинах: 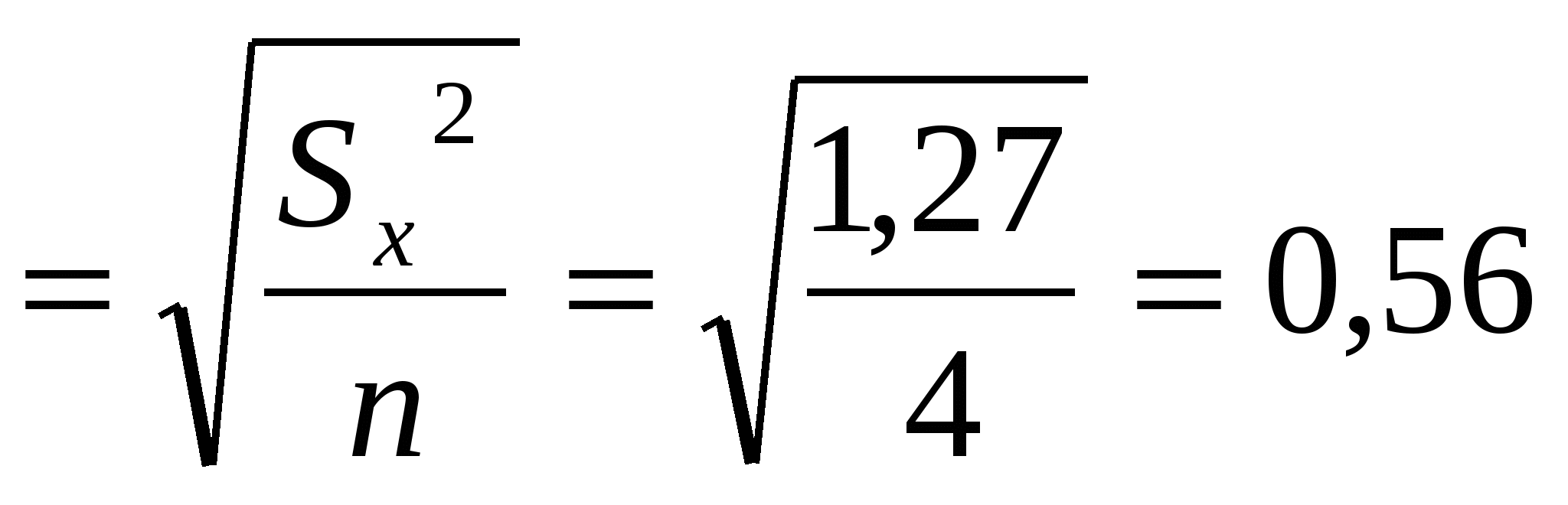  ц;2. Ошибка разности средних:   ц3. Наименьшая существенная разность для принятого уровня значимости 05: ц,Значение критерия  находим по прил. 2 по числу степеней свободы для остаточной (случайной) дисперсии Заключение. Разность между средними  считается существенной, когда ≥ . Если < , разность несущественная, т.е. она не выходит за пределы ± и, следовательно, находится в пределах ошибки опыта. В данном примере при 5%-ом уровне значимости прибавки урожаев во втором и третьем вариантах существенны.Урожайность в варианте с осенней плоскорезной обработкой почвы на 20-22 см (вариант 2) составила 16,0 ц/га, в варианте с осенней вспашкой на 20-22 см (контроль) – 14,0 ц/га. Разница ( ) между урожайностями 2,0 ц/га и она превышает 05=1,8 ц/га. Урожайность в варианте с осенней плоскорезной обработкой на 10-12 см (вариант 3) по сравнению с контролем выше на 3,8 ц/га, что тоже превышает 05. Дисперсионный анализ с применением корректирующего фактора (модель 2-я) Одним из методов расчёта сумм квадратов отклонений для разных видов варьирования является способ произвольного начала. Применяется он при обработке многозначных цифр и отсутствии счётных машин. Сущность его заключается в том, что отклонения поделяночных урожаев Х находят не от среднего урожая по опыту  (как уже было рассмотрено), а от условной средней величины А (произвольного начала). За условную среднюю берут любое целое число, близкое к среднему урожаю по опыту. Это значительно упрощает вычисление отклонений и сводит ошибки при расчётах к минимуму. Технику расчёта рассмотрим на том же самом примере Поделяночная урожайность пшеницы в опыте со способами обработки почвы
1-й этап. Составляют таблицу урожаев и проверяют правильность вычислений так же, как и в предыдущем случае (∑V=∑Р=∑Х=250,6). 2-й этап. Выбирают произвольное начало (условную среднюю А = 16), составляют таблицу отклонений поделяночных урожаев от произвольного начала  . Правильность вычислений проверяют по равенству  Все поделяночные отклонения и суммы отклонений по вариантам  и повторениям  возводят в квадрат.Находят суммы квадратов для разных видов варьирования, но предварительно определяют общее число наблюдений в опыте и корректирующий фактор (поправку). Общее число наблюдений  ;корректирующий фактор –  ;виды варьирований (суммы квадратов): общее  по повторениям  ;по вариантам  ;остаточные (ошибки)  .Таблица отклонений и квадратов отклонений от произвольного начала А=16
3-й этап. Составляют таблицу дисперсионного анализа. Все последующие вычисления проводят так же, как и в предыдущем случае. Таблица дисперсионного анализа
В данном примере ≥ , что указывают на наличие существенных различий между вариантами на 5%-ном уровне значимости.Вычисляют показатели, характеризующие существенность различий между вариантами: ошибка опыта в абсолютных величинах: 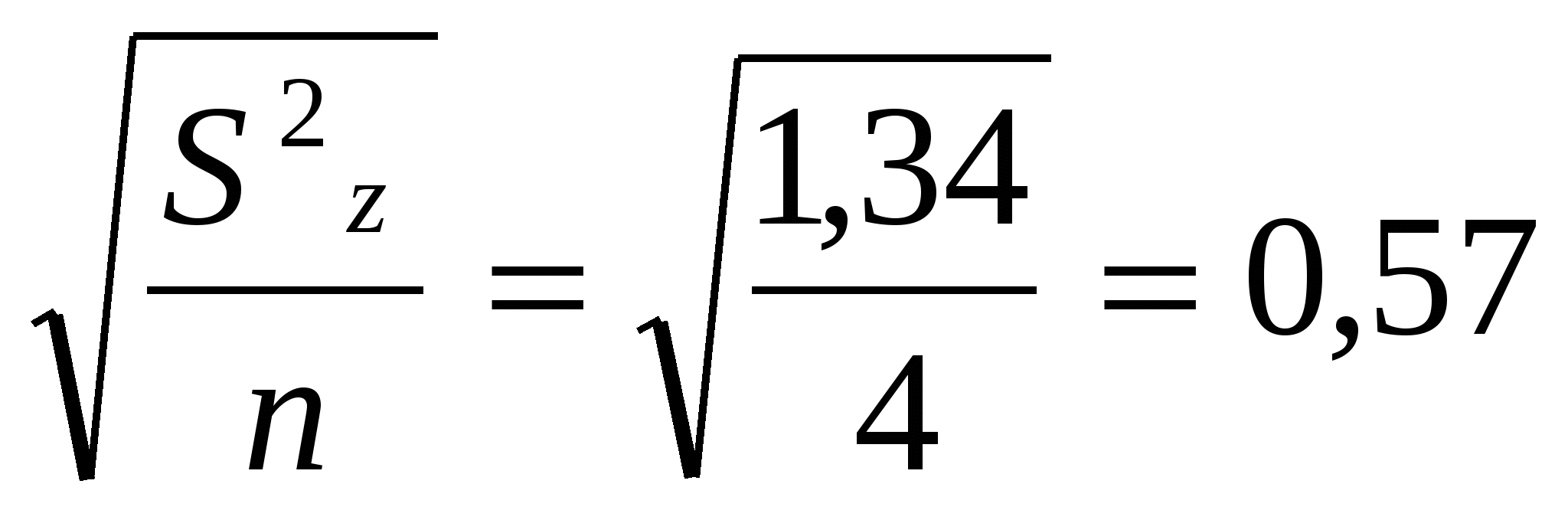 = ц;ошибка разности  ц.Наименьшая существенная разность ( ): .Дисперсионный анализ с использованием условной средней (А), равной нулю (модель 3-я) При этом методе расчёта суммы квадратов отклонений вычисляются по фактическим данным, т.е. при произвольном начале А=О. Порядок расчётов рассмотрим на том же примере Поделяночная урожайность яровой пшеницы в опыте со способами обработки почвы
Общее число наблюдений ; корректирующий фактор  ;виды варьирований (суммы квадратов): общее  по повторениям  ;по вариантам  ;остаточное (ошибки)  .Суммы квадратов по видам варьирования получены такие же, как и в предыдущем методе расчёта, так как были использованы одни и те же исходные данные. Последующие расчёты заключаются в составлении таблицы дисперсионного анализа и определении показателей, характеризующих существенность частных различий. Проводятся они так же, как и ранее. ЛЕКЦИЯ № 8. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
)
)
)
)
=250,6
=15,7