Курс лекций по основам. Роль с Х. науки в развитии апк страны
 Скачать 1.33 Mb.
|
|
Тема. Корреляционный и регрессионный анализ экспериментальных данных План
В сельскохозяйственных и биологических исследованиях часто выясняют взаимосвязь между изучаемыми признаками. Для измерения силы (тесноты) и формы связи используют специальные статистические методы – корреляцию и регрессию. Все значения одного признака являются случайными переменными. Один из признаков принимают за аргумент (независимую переменную Х), другой за функцию (зависимую У). Любому значению Х может соответствовать любое значение У, следовательно, корреляционная зависимость должна устанавливаться на основе достаточно большого числа пар наблюдений. Корреляция – это вероятностная связь. Она бывает простой и множественной; по форме линейной и криволинейной, по направлению прямой обратной. Линейная корреляция – это зависимость, при которой с увеличением средней величины одного признака увеличивается средняя величина другого, или наоборот, с увеличением средней величины одного уменьшается средняя величина другого. В первом случае корреляция будет прямой (положительной), во втором обратной (отрицательной). При криволинейной корреляции результативный (зависимый) признак с увеличением факториального (независимого) возрастает до определённой величины, а затем убывает или наоборот. При простой корреляции исследуется связь между двумя признаками. Множественная корреляция наблюдается, если на величину одного признака влияет несколько факториальных. Наибольшее распространение имеет простая линейная корреляция. Степень связи между признаками обычно выражается отвлечённым числом, которое при прямолинейной зависимости называется коэффициентом корреляции. Расчету коэффициента корреляции должен предшествовать первичный анализ данных наблюдений. Материал наблюдений надо проанализировать с точки зрения соответствия данных общим закономерностям изменения того или иного явления и его взаимосвязи с другими явлениями. После анализа и отбраковки явно нетипичных данных составляют таблицу – сводку, где Х обозначает независимую переменную (аргумент), У – зависимую переменную (функцию). Последовательность расчётов при корреляционном анализе Рассчитываются следующие показатели: r – коэффициент корреляции dу/х - коэффициент детерминации Sd - ошибка коэффициента корреляции tr факт.- критерий существенности (значимости) корреляции r – коэффициент корреляции служит для измерения силы (тесноты, степени) и направления линейной связи. Изменяется от -1 до +1. считается, что при: r = 0 линейная (прямолинейная) связь между изучаемыми признаками отсутствует (может быть, криволинейная связь). r = 0 – 0,3 – связь слабая r = 0,3 = 0,7 – связь средняя r = 0,7 = 1,0 – связь сильная (тесная) Для положительных (или прямых) связей, коэффициент корреляции (r), со знаком (+) будет означать, что с увеличением суммы осадков, увеличивается урожай. Для отрицательных (обратных) связей знак (-) означает, что при увеличении суммы осадков, снижается урожай. При полных связях , когда корреляционная связь превращается в функциональную, r – для прямых (положительных) связей равен (+1), а для обратных (отрицательных) связей равен (– 1) Чем ближе r к (+1) или к (-1), те сильнее (теснее) линейная (прямолинейная) корреляционная связь. Вычисление коэффициента корреляции между количеством осадков во II и III декадах июня (Х) и урожаем (У) яровой пшеницы
 ;  1. Коэффициент корреляции для выборочных наблюдений вычисляют по формул   = .Не вычисляя отклонения и квадраты отклонений, корреляцию можно рассчитать по формуле  ,где  – число сопоставляемых пар (объём выборки).2. Степень связи между признаками более точно измеряется коэффициентом детерминации  , равным квадрату коэффициента корреляции ( ) и показывающим долю тех изменений (%), которые зависят от изучаемого фактора. В нашем примере при =0,8 не 80%, а только 64% изменчивости признака У обусловлена действием факториального признака Х ( ), остальная часть корреляционной связи ( ) обусловлена другими факторами.3. Коэффициент корреляции выборочных наблюдений подвержен случайным колебаниям, которые зависят как от особенностей образования выборки, так и от точности наблюдений. Поэтому для оценки надёжности определяют его ошибку  и критерий существенности  : ;  где – ошибка коэффициента корреляции; – число сопоставляемых пар (объём выборки).С увеличением объёма выборки уменьшается, а точность определения возрастает.Критерий существенности коэффициента корреляции определяют по формуле  Если  , то корреляционная связь существенна, а при  <  – несущественна. находят по табл. приложения 2 для 5%-ного, а при более строгом подходе – 1% - ного уровня значимости. Число степеней свободы принимают равным v  . В нашем примере при v=  ,  и  корреляционная связь существенна при 5%-ном и 1%-ном уровне значимости, так как .При достаточно большом числе наблюдений (не менее 100) коэффициент корреляции считается существенным, если он превышает свою ошибку в три и более раза, т.е. когда  .Регрессионный анализ При корреляционном анализе с помощью коэффициента корреляции можно выяснить тесноту (силу) и направление связи, но нельзя узнать, как количественно меняется результативный признак при изменении факториального на единицу измерения. Эта задача решается с помощью регрессионного анализа. Регрессия – это изменение результативного признака (зависимой переменной, или функции У) при определённых изменениях факторного признака (независимой переменной или аргумента Х). Различают регрессию простую и множественную, по форме - линейную и криволинейную. Сущность регрессионного анализа состоит в том, чтобы построить линию (прямую в случае прямолинейной зависимости), которая наиболее точно выражала бы зависимость одного признака от другого. Зависимость функции от аргумента при линейной регрессии выражается коэффициентом регрессии (в), который показывает, как в среднем изменяется (увеличивается или уменьшается, смотря по знаку в) результативный признак (функция) при изменении факториального признака (аргумента) на одну единицу измерения. Коэффициенты линейной регрессии вычисляются по формулам:  и  .В нашем примере  , .Коэффициенты регрессии имеют знак коэффициента корреляции. Произведение коэффициентов регрессии равно квадрату коэффициентов корреляции (что используется для проверки расчётов коэффициентов регрессии):  ;  .Чаще всего из двух коэффициентов регрессии вычисляют только один. При исследовании односторонней зависимости, например корреляции между урожаем У и количеством выпавших осадков Х (как в нашем примере), вычисляют только один коэффициент регрессии результативного признака  , который показывает, как изменяется У при изменении Х на единицу измерения; выражается он в единицах У. Так с увеличением количества осадков во II и III декадах июня на 1 мм урожайность яровой пшеницы повысится на 0,34 ц/га. Вычисление 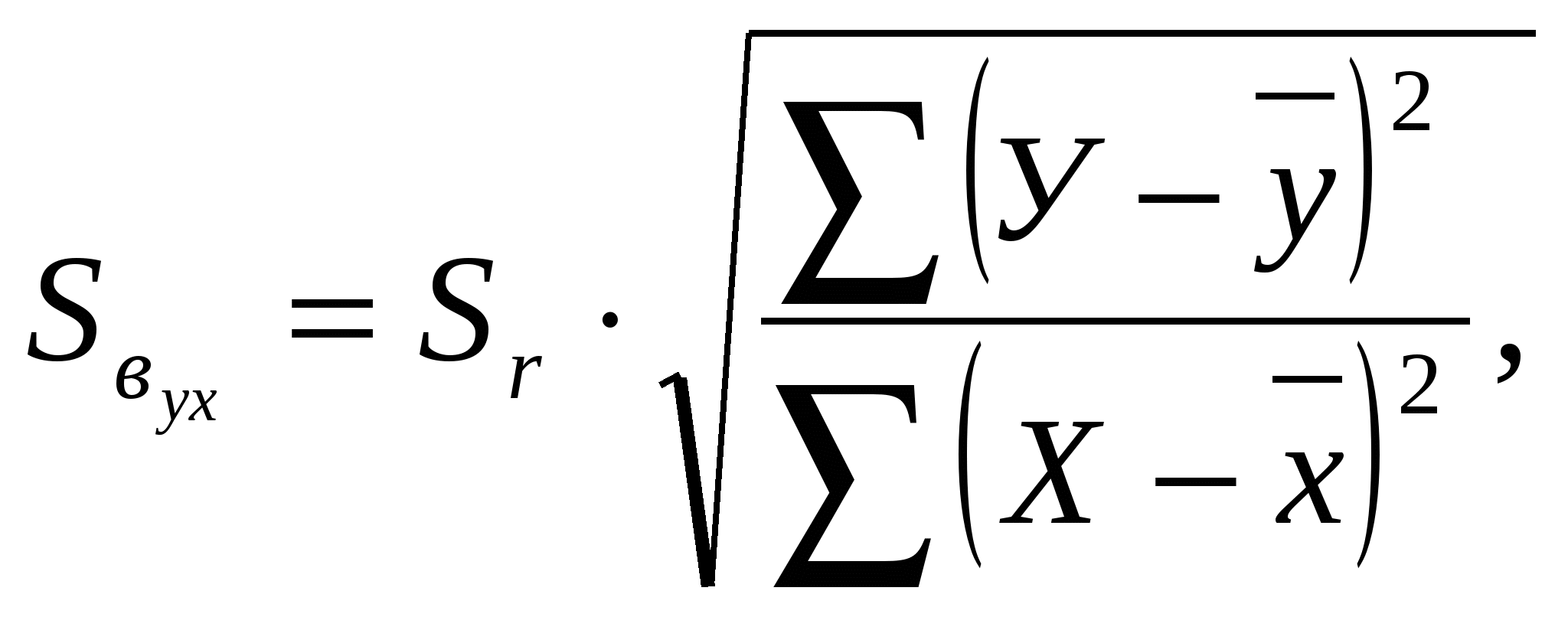 лишено смысла, мы его рассчитали для проверки вычислений коэффициентов регрессии. Затем находят ошибку коэффициента регрессии:  .Критерий существенности коэффициента регрессии равен:    и  мы не вычисляем, так как в данном примере  , что свидетельствует о существенности регрессии.Сопоставляя значения  и  можно при заданном уровне значимости (05 или 01) и числе степеней свободы v оценить существенность коэффициента регрессии результативного признака – . Если известен критерий существенности коэффициента корреляции и значимость его доказана, то существенным будет и коэффициент регрессии, так как .Для наглядности корреляцию можно изобразить в виде линии регрессии. Теоретическую линию регрессии можно построить двумя способами: - графическим (с помощью прозрачной линейки), позволяющим приближённо выявить лишь общую тенденцию зависимости; - аналитическим, используя уравнение линейной регрессии У по Х:  где  и  - средние арифметические признаков Х и У; -коэффициент регрессии результативного признака.Подставляя в это уравнение вычисленные значения , и , определяют формулу уравнения прямой линии  ;  Подставляя значения  и , получим: По этому уравнению определяют теоретические усреднённые значения У (табл.23) для всех фиксированных значений Х (иногда ограничиваются определением значений У только для Xmin и Xmax). Вычисление теоретических значений У
На графике откладывают значения признака Х и сопряжённые фактические значения признака У. Найдённые координаты соединяют кривой и получают эмпирическую линию регрессии. Так как на варьирование значений результативного признака в опыте оказывает влияние ряд случайных причин, то эмпирическая линия регрессии, как правило, имеет форму ломаной линии. Поэтому надо построить прямую (теоретическую линию регрессии), которая позволяет определить любое значение результативного признака по заданному значению признака Х. Выводы.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=502
=5257
