Курс лекций по основам. Роль с Х. науки в развитии апк страны
 Скачать 1.33 Mb.
|
|
ТЕМА. Многофакторный полевой опыт и обработка его результатов методом дисперсионного анализа Опыт, в котором изучается действие 2-х и более факторов одновременно называется многофакторным или сложным. В этих опытах кроме действия факторов на урожайность, устанавливают величину и характер взаимодействия этих факторов. 1-й фактор (А) – внесение навоза а) с внесением навоза б) без внесения навоза (ℓА = 2) 2-й фактор (В) - минеральные удобрения а) без удобрений б) азотные в) фосфорные г) калийные д) сочетание NPK (ℓВ = 5) Многофакторные опыты чаще всего ставят методом расщеплённых или сложных делянок. 1-е повторение
А0 А1 Делянки первого порядка Фактор А, ℓА = 2 1. Без внесения навоза – А0 2. С внесением навоза - А1 Делянки второго порядка Фактор В, ℓВ = 5 1. Без удобрений В0 2. Азотные В1 3. Фосфорные В2 4. Калийные В3 5. Сочетание ΝPK В4 В многофакторном опыте изучается не только действие, но и устанавливают величину и характер взаимодействия (dА dВ dАВ) изучаемых факторов. В зависимости от изучаемых факторов, характер взаимодействия может быть: 1. Положительным (синергизм). При этом прибавка урожая от совместного применения факторов больше арифметической суммы прибавок от раздельного применения факторов. +dA+B > (+dA) + (+dB) 2. Отрицательным (антогонизм). При этом прибавка урожая от совместного применения факторов меньше арифметической суммы прибавок от раздельного применения факторов. +dA+B < (+dA) + (+dB) 3. Факторы не взаимодействуют (аддитивизм). При этом прибавка урожая от совместного применения факторов примерно равна арифметической сумме прибавок от раздельного применения факторов. +dA+B ≈ (+dA) + (+dB) Чаще всего для оценки существенности влияния изучаемых факторов и их взаимодействия используют метод дисперсионного анализа. Метод дисперсионного анализа данных многофакторного полевого опыта, поставленного методом расщеплённых (сложных) делянок В опытах с расщеплёнными делянками имеется большие делянки первого порядка, которые расщепляются (делятся) на более мелкие делянки второго порядка и т.д. Статистическая обработка данных таких опытов имеет свою специфику, так как ошибки на больших и малых делянках неодинаковы по величине и поэтому оценка существенности разниц по одному значению  не может быть правильной. Первоначальную обработку данных этих опытов проводят в той же последовательности, что и обработку данных многофакторного опыта поставленного методом рендомизированных повторений. Отличием здесь является разложение остаточной суммы квадратов  на вариабельность делянок первого (ошибка I), второго (ошибка II) и т.д. порядков.Рассмотрим технику вычислений при дисперсионном анализе данных двухфакторного опыта 3х2 по изучению влияния предшественника и удобрений на урожайность яровой пшеницы. На делянках первого порядка (главные делянки) изучалось действие предшественника (0-горох, 1- подсолнечник, 2-кукуруза, 3-однолетние травы), а на делянках второго порядка (субделянки) – два фона питания растений (0 – Без навоза, 1- Навоз. Расчёты при дисперсионном анализе проводят только по третьей модели (рассчитывают поправку или корректирующий фактор). Расчёты выполняются в несколько этапов: 1-й этап Составляют таблицу урожаев и рассчитывают в ней суммы урожаев по вариантам (∑V), по повторениям (∑Р), средние урожаи по варианта (ХV), сумму поделяночных урожаев (∑Х) и среднюю урожайность по опыту Хо=  Таблицу урожаев проверяют по равенству ∑P = ∑V = ∑Х = одно число
Вводится корректирующий фактор С =  Количество делянок вычисляют по формуле Ν = ℓА× ℓВ × n или 2 ×5×4=40 2-й этап. Вычисляют виды варьирований (или суммы квадратов): а) общая сумма квадратов Су = ∑Х2 – С б) сумма квадратов по повторениям СР = ∑Р2 : (ℓА×ℓВ) – С в) сумма квадратов по вариантам СV = ∑V2 : n - C г) сумма квадратов для случайной ошибки СZ = CУ – (СР+СV) 3-й этап. Определяют суммы квадратов для факторов А (навоз), В (удобрения) и АВ (их взаимодействие), т.е. варьирование урожаев в зависимости от действия факторов А, В и взаимодействия АВ. (СА, СВ, САВ) Таким образом, общее варьирование вариантов разъединяется С V = СА + СВ + САВ Для этого составляют вспомогательную таблицу. В неё записывают суммы урожаев по вариантам (из таблицы №1), находят суммы и средние по факторам А и В. Таблица №2 Суммы урожаев для определения главных эффектов и взаимодействия
СА = ∑А2 : (ℓв×n) – С при степени свободы υА = ℓА – 1 = 2 – 1 = 1 СВ = ∑В2 : (ℓА×n) – С при степени свободы υВ = ℓВ – 1 = 5 – 1 = 4 САВ = СV – (СА+ СВ) при степени свободы υАВ = (ℓА – 1)×ℓВ – 1) Таким образом, в 2-х факторном опыте, поставленным методом организованных повторений, сумма квадратов (СV) расчленяется на три компонента СV = СА + СВ + САВ В 3-х факторном опыте – на семь компонентов: Сv = СA + СB + СC + СAB + СAC + С BC + СABC Соответственно и общая сумма квадратов СУ равна: - в двухфакторном опыте Су = СА + СВ + САВ + СР + СZ  - в трёхфакторном опыте СУ = СА + СВ + СС + САВ + САС + СВС + САВС 4-й этап. Находят суммы квадратов для остатка (ошибки) СZ = СZ1 + СZII В двухфакторном опыте, поставленного методом расщеплённых делянок, имеется две ошибки: - одна для вариантов по фактору А (изучаются на более крупных делянках I порядка) Ошибка I. - вторая, ошибка II – для вариантов по фактору В и взаимодействия АВ. Таким образом, общее остаточное варьирование разделяется на компоненты СZ = СZI + CZII а) сумма квадратов CZI даёт возможность оценить существенность действия по вариантам фактора А (действие навоза). (Ошибка I) б) эффективность минеральных удобрений и взаимодействия удобрений с навозом. (Ошибка II). СZI – вычисляют, а СZII –находят по разности СZII = СZ - СZI Чтобы найти CZI составляют вспомогательную таблицу, куда записывают суммы урожаев по делянкам I – го порядка (навоз). Таблица 3 Суммы урожаев по делянкам 1-го порядка для вычисления ошибки I
Из этой таблицы находят общую сумму квадратов для делянок 1-го порядка - СУI - СУI – включает в себя варьирование повторений (СР) и случайное варьирование для делянок 1-го порядка (СZI). Таким образом: СУI = СА + СР + СZI СZI = СУI – (СА + СР) при υ = (ℓА – 1)×(n – 1) СУI = ∑ХА : ℓВ – С СZII = СZ - СZI υ = (2 – 1)×(4 – 1_= 3 Далее составляют таблицу дисперсионного анализа двухфакторного опыта (2×5), поставленного методом расщеплённых делянок Таблица 4
Fф – находят в таблице приложения рабочей тетради, исходя из числа степеней свободы соответственно для факторов А, В и взаимодействия АВ. Ошибка II соответствует факторам В и взаимодействия АВ (она одинакова). 5 этап. Оценка существенности частных различий а) Делянки 1-го порядка (эффект применения навоза) Рассчитывают абсолютную ошибку и ошибку разности: S¹х = ±  z ı и S¹d = ± z ı Затем рассчитывают НСР¹05 = t05 × S¹d t – берут из таблицы при υz ı = 3 Штрих означает, что это для делянок 1-го порядка (действие навоза) б) Делянки 2-го порядка (эффект применения удобрений Sllх = ± zıı и Sııd = ±z ıı Затем рассчитывают НСРII05 = t05 × Slld t – берут из таблицы при υzıı = 24 6 этап. Оценка существенности главных эффектов а) Для главного эффекта применения навоза (фактор А). SАd = 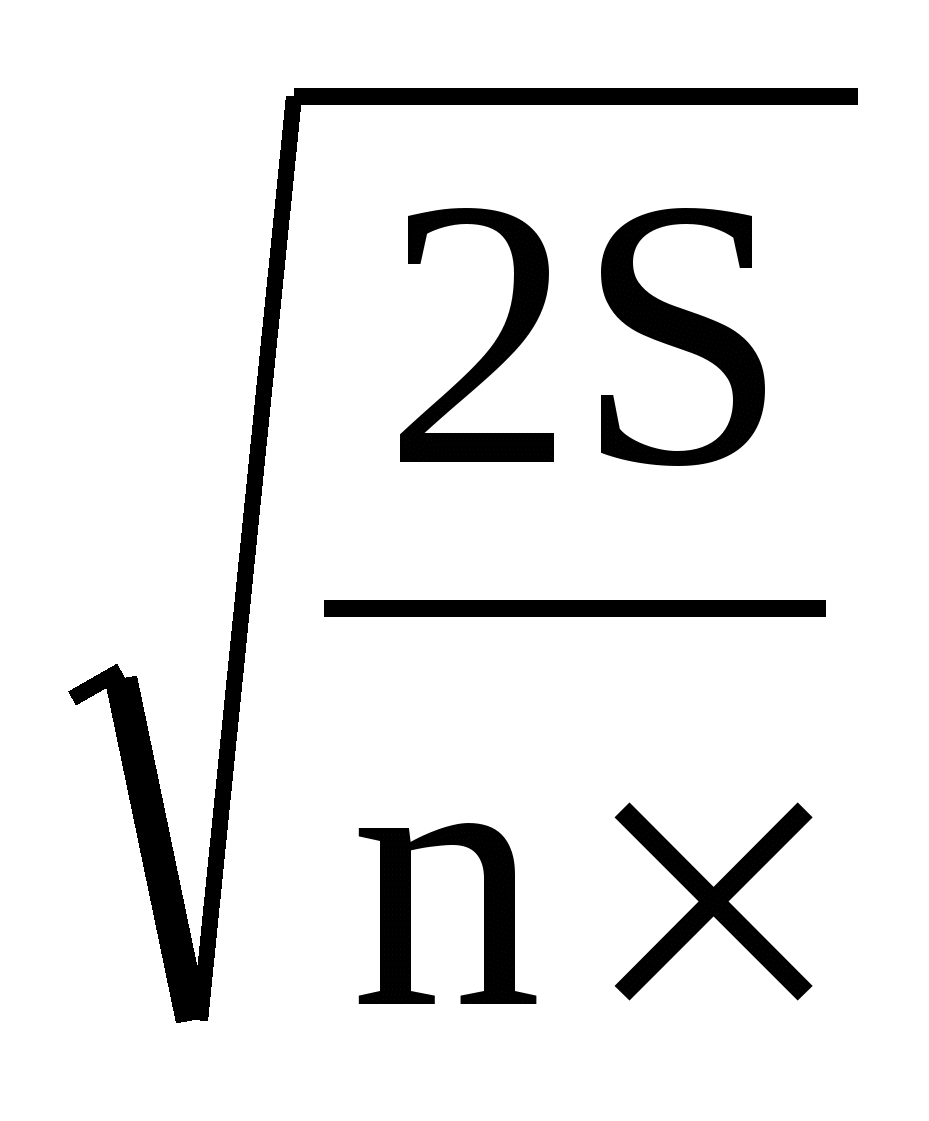 Z ı НСРА05 = t05 × SАd t05 – берут из таблицы при υz ı = 3б) Для главного эффекта применения удобрений (фактор В). SdВ,АВ = 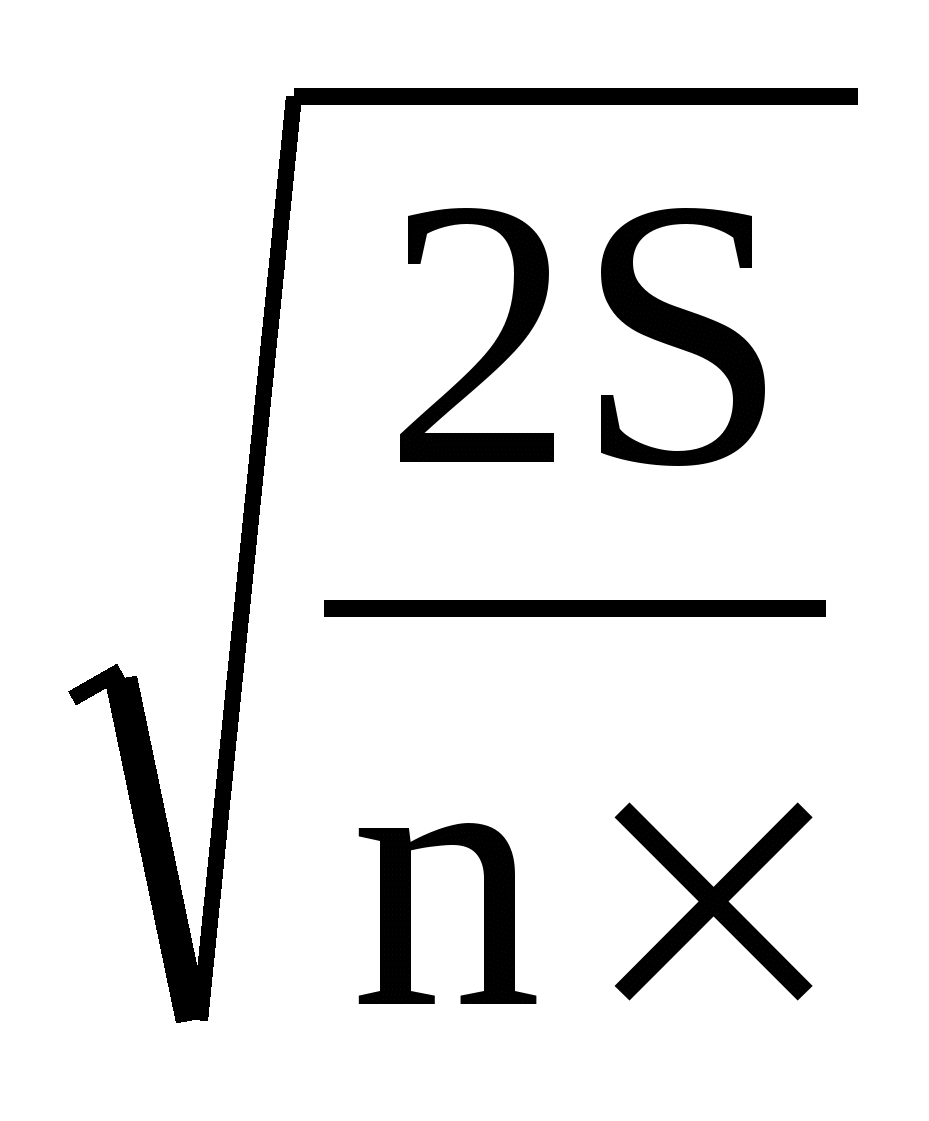Z ıı НСР05В,АВ = t05 × SdВ,АВ t05 – берут из таблицы при υz ıı = 24Заключение. Полученные значения НСРI05, НСРII05, НСРА05 и НСРВ05 используют: (Анализ таблицы № 1) По НСРI05 – оценивают значимость разностей между частными средними для делянок 1-го порядка т.е. эффект навоза при разных видах минеральных удобрений. а1в0 - а0в0 - эффект навоза без удобрений а1в4 - а0в4 - эффект навоза + NPK а1в1 - а0в1 - эффект N удобрений + навоз (на фоне навоза) а1в2 - а0в2 - эффект Р удобрений на фоне навоза а1в3 - а0в3 - эффект К удобрений на фоне навоза Таким образом, устанавливаем эффект навоза при применении разных минеральных удобрений. По НСРII05 оценивают существенность (значимость) разностей между частными средними по делянкам 2-го порядка т.е. эффект минеральных удобрений на разных фонах навоза (с навозом и без навоза). а0в1 - а0в0 - эффект N удобрений на фоне без навоза а1в1 - а1в0 - эффект N удобрений на фоне с навозом а0в2 - а0в0 - эффект Р удобрений на фоне без навоза а1в2 - а1в0 - эффект Р удобрений на фоне с навозом а0в3 - а0в0 - эффект К удобрений на фоне без навоза а1в3 - а1в0 - эффект К удобрений на фоне с навозом а0в4 - а0в0 - эффект NPК на фоне без навоза а1в4 - а1в0 - эффект NPК на фоне с навозом (Анализ таблицы №2. «Определение главных эффектов и взаимодействия). По НСРА05 оценивают существенность (значимость) среднего (главного) эффекта фактора А (навоза), не зависимо от видов минеральных удобрений. А1 – А2 = dА По НСРВ05 оценивают значимость (существенность) среднего (главного) эффекта минеральных удобрений (фактор В) не зависимо от фона В1 – В0 = d1в В2 – В1 = d2в В3 – В2 = d3в В4 – В3 = d4в ЛЕКЦИЯ № 9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||