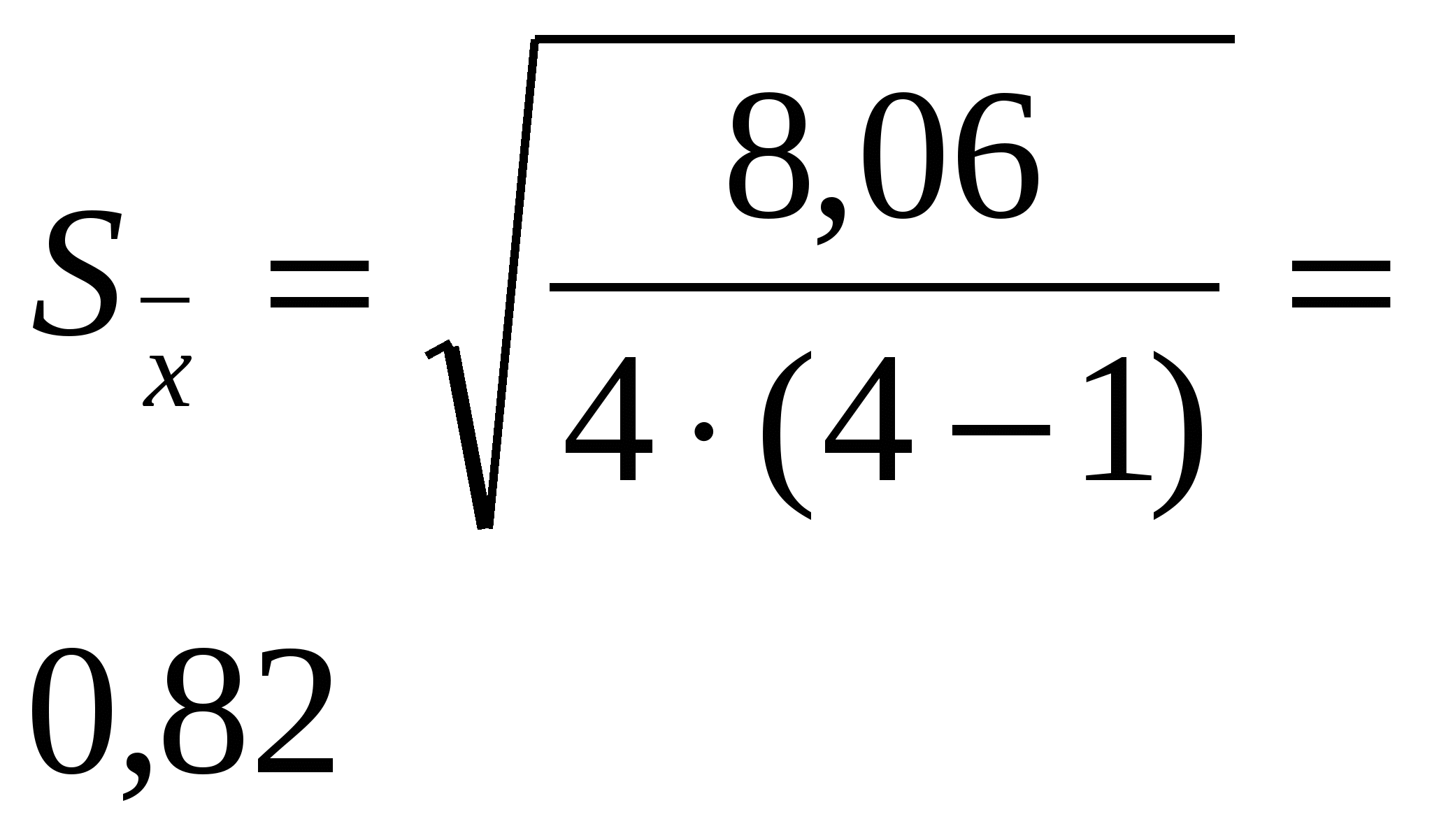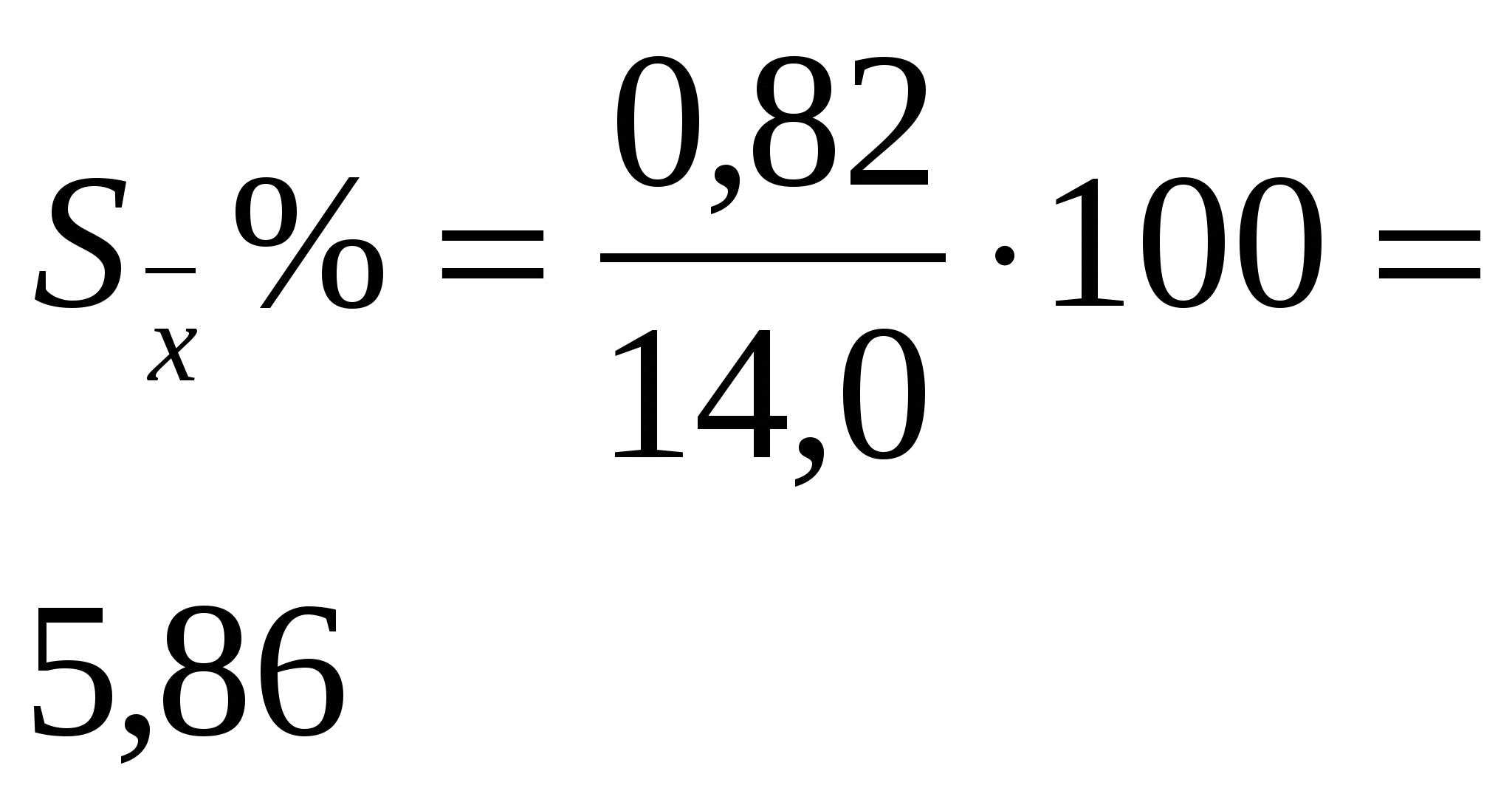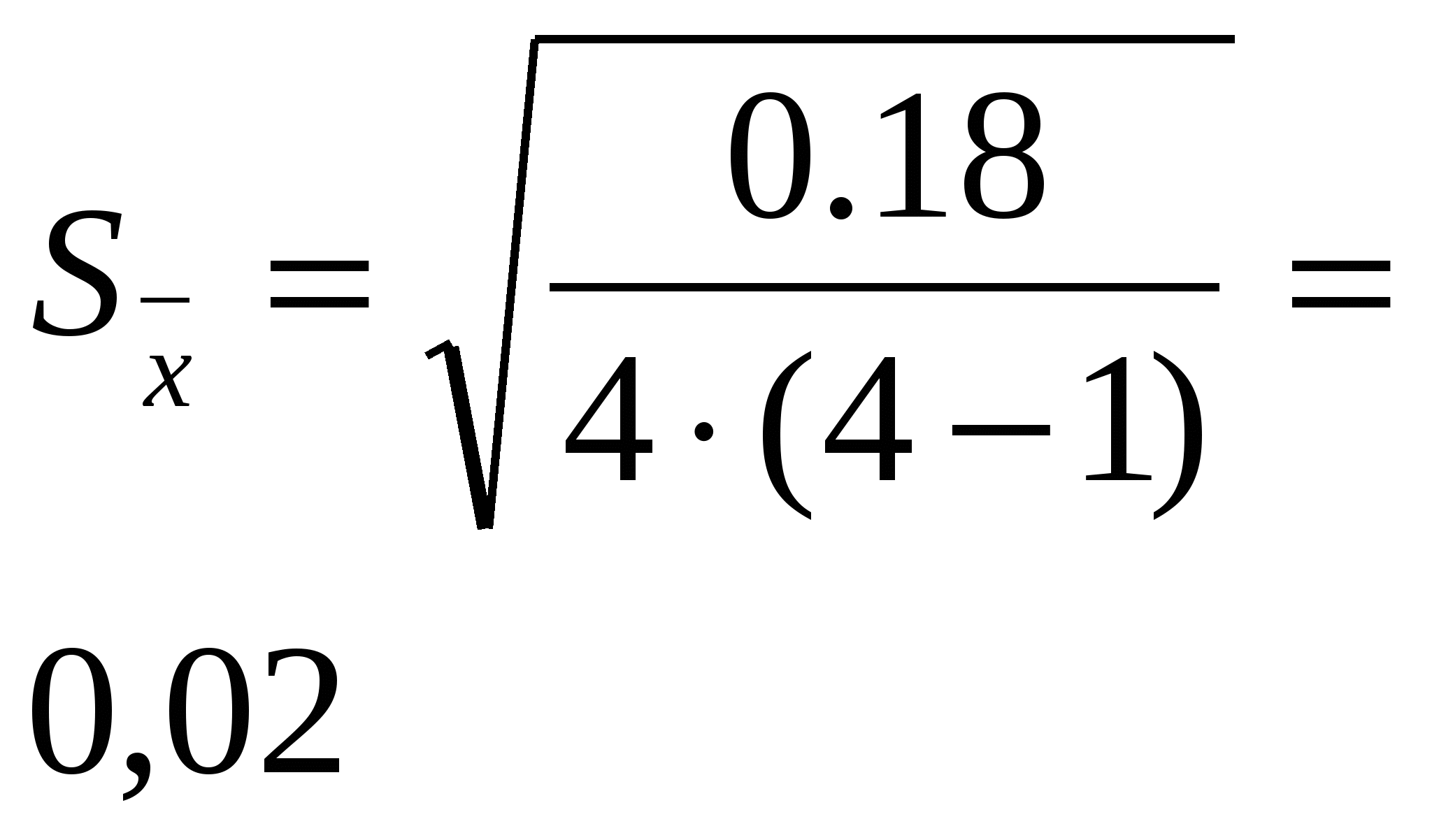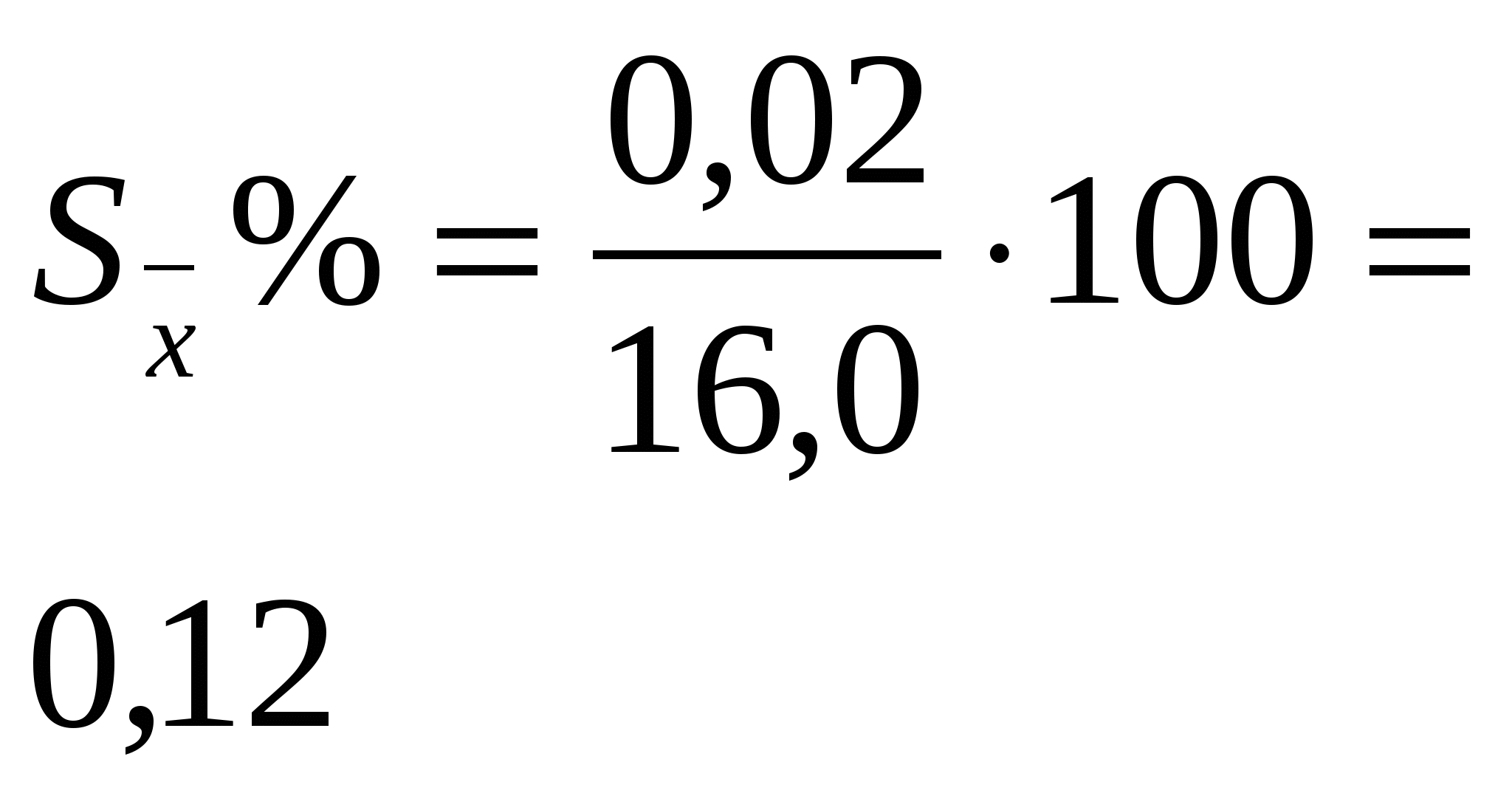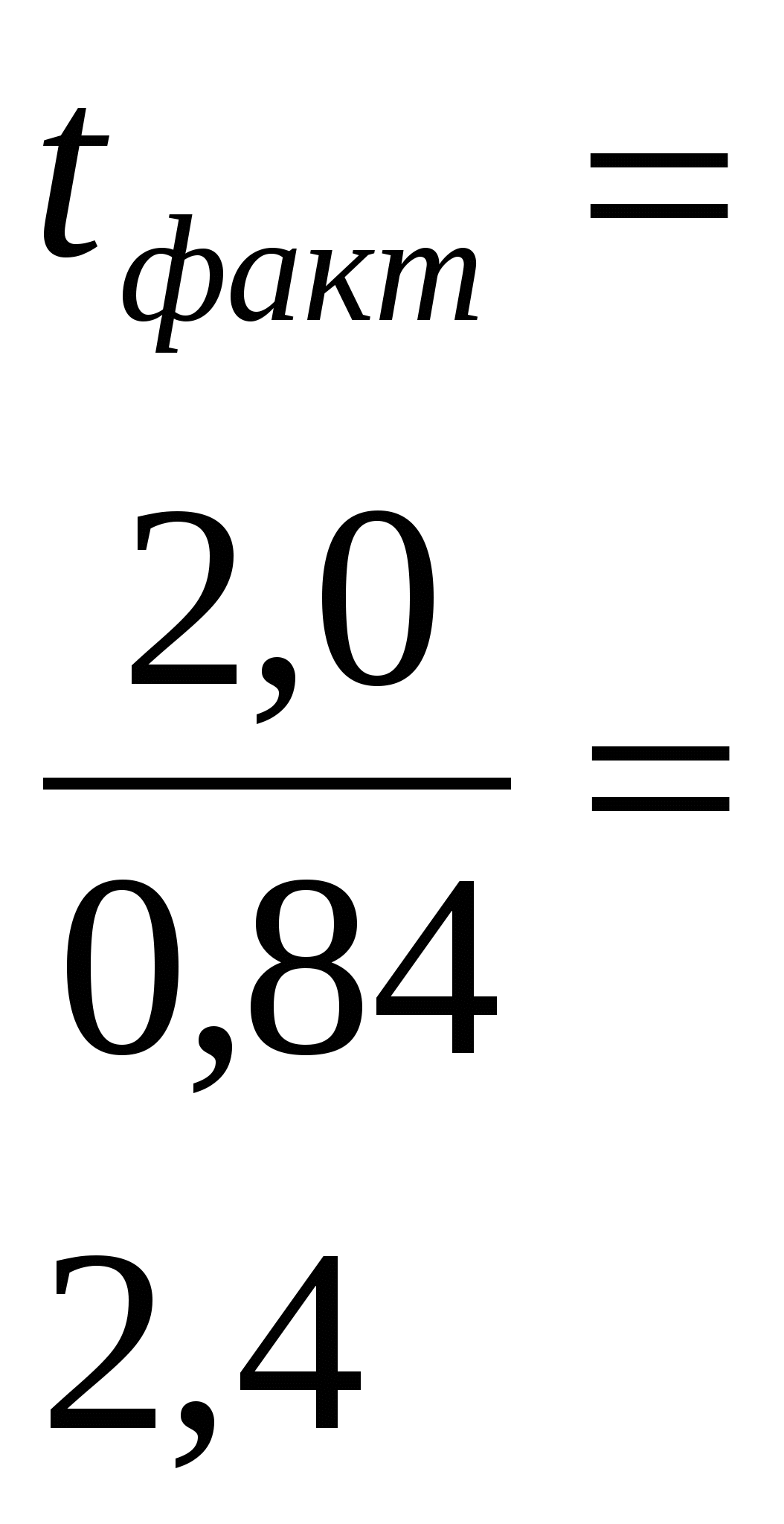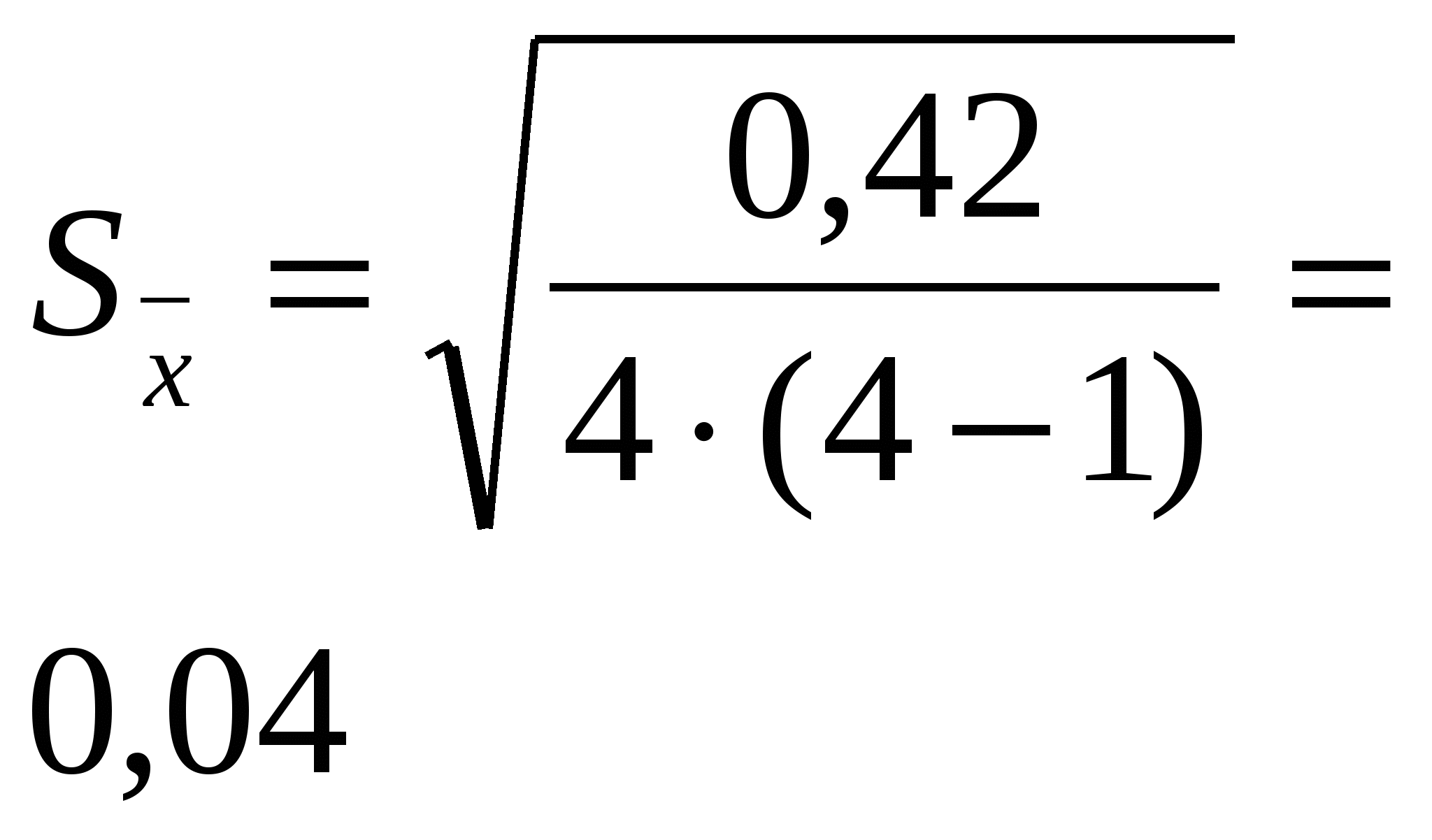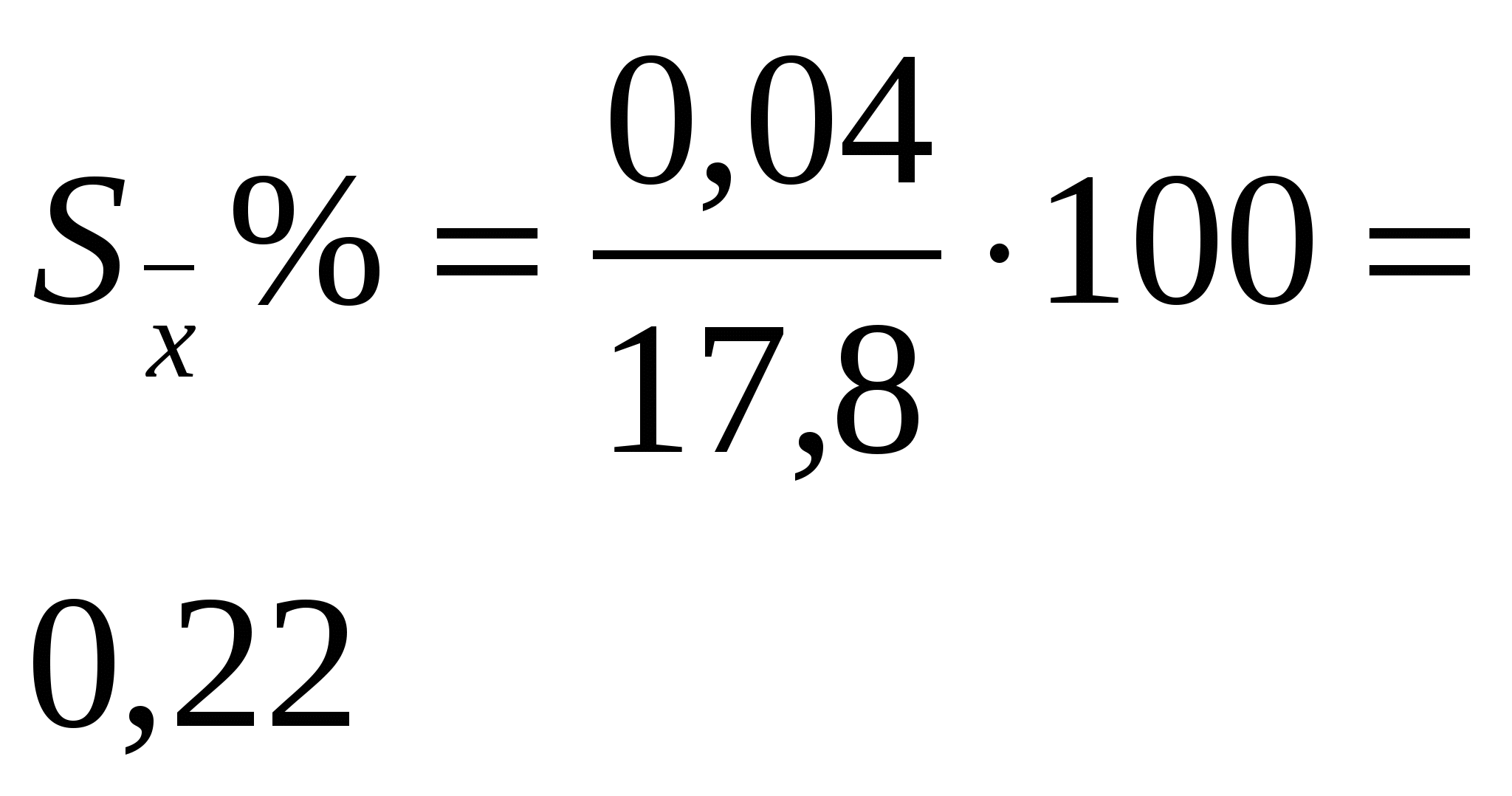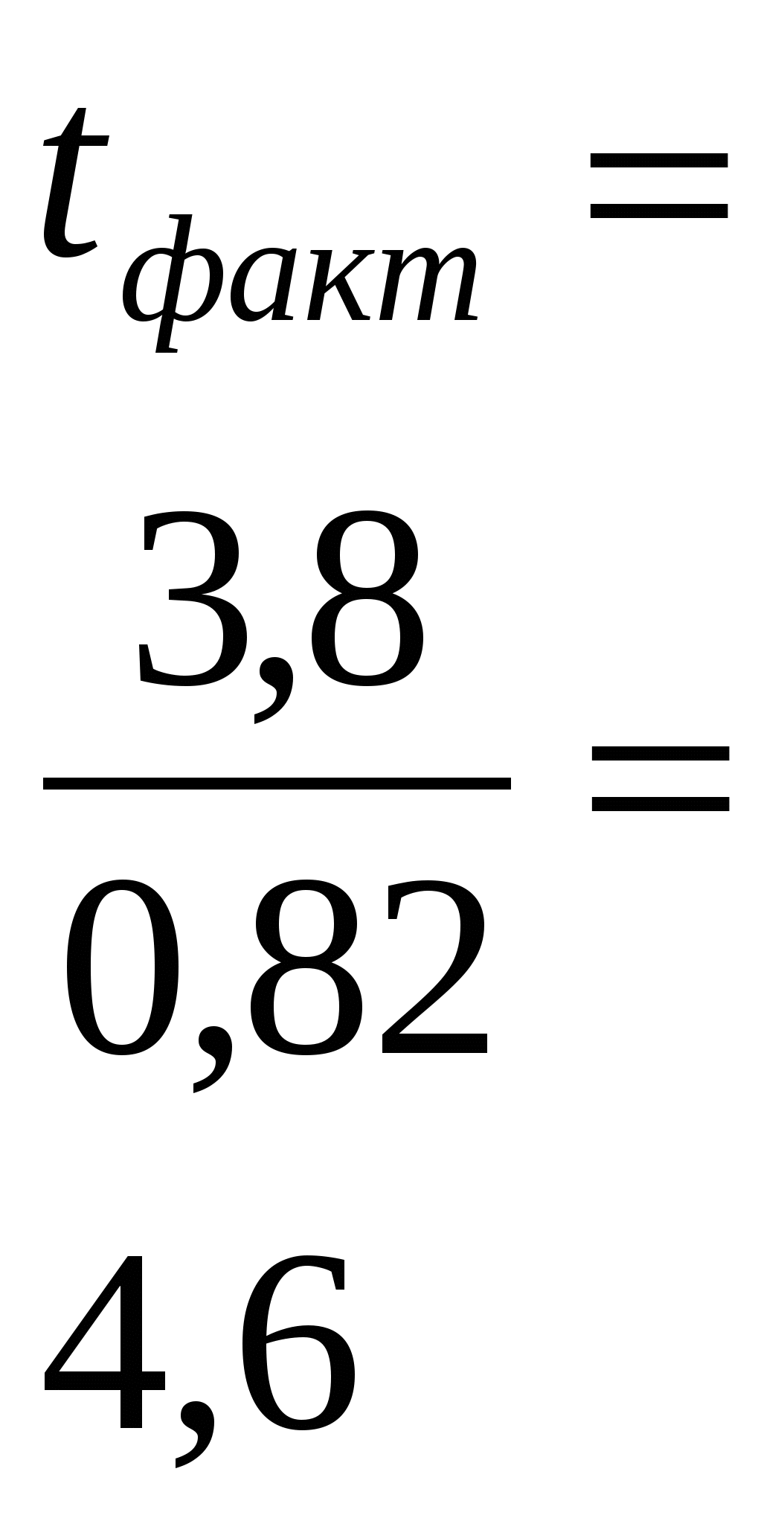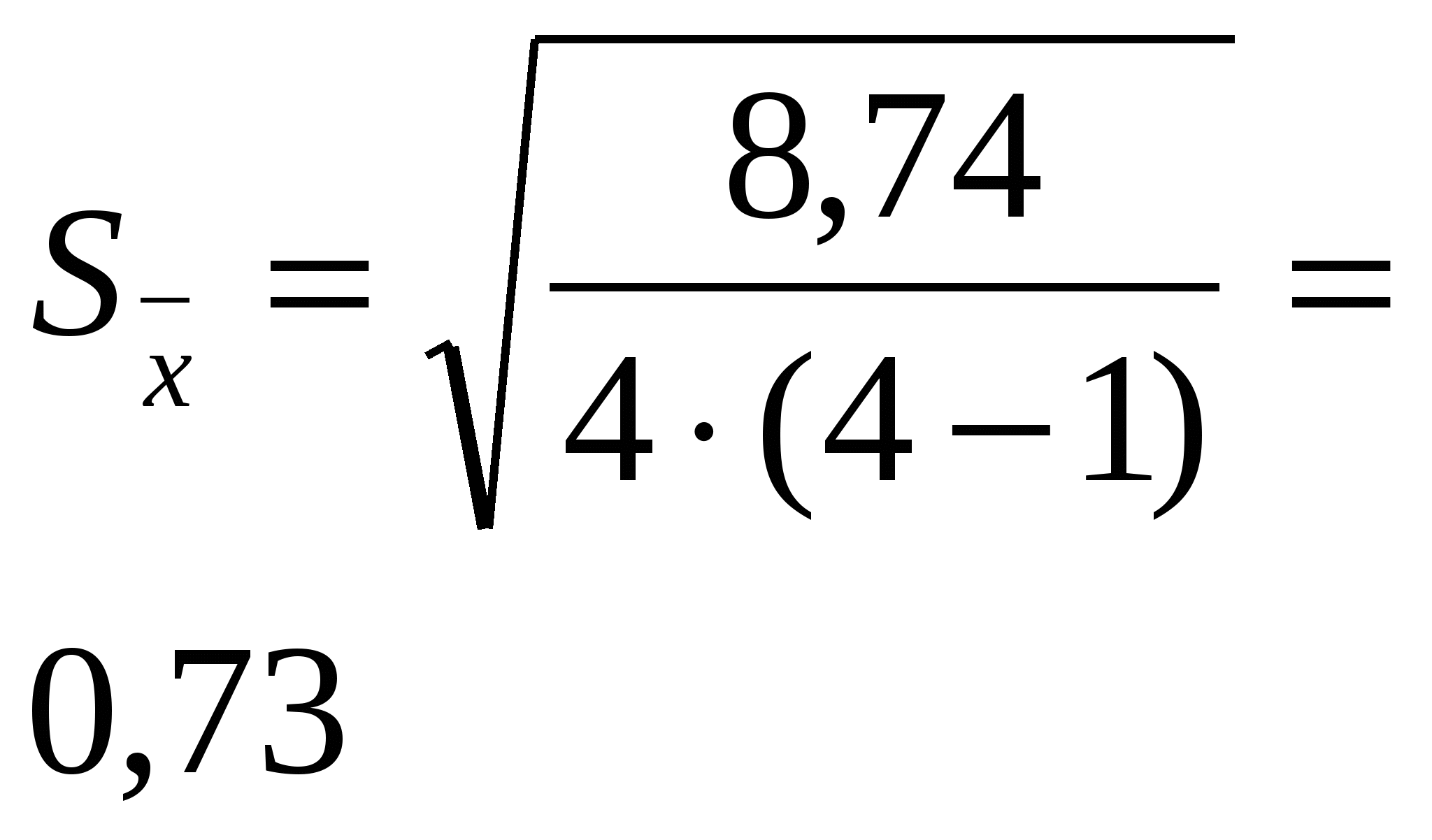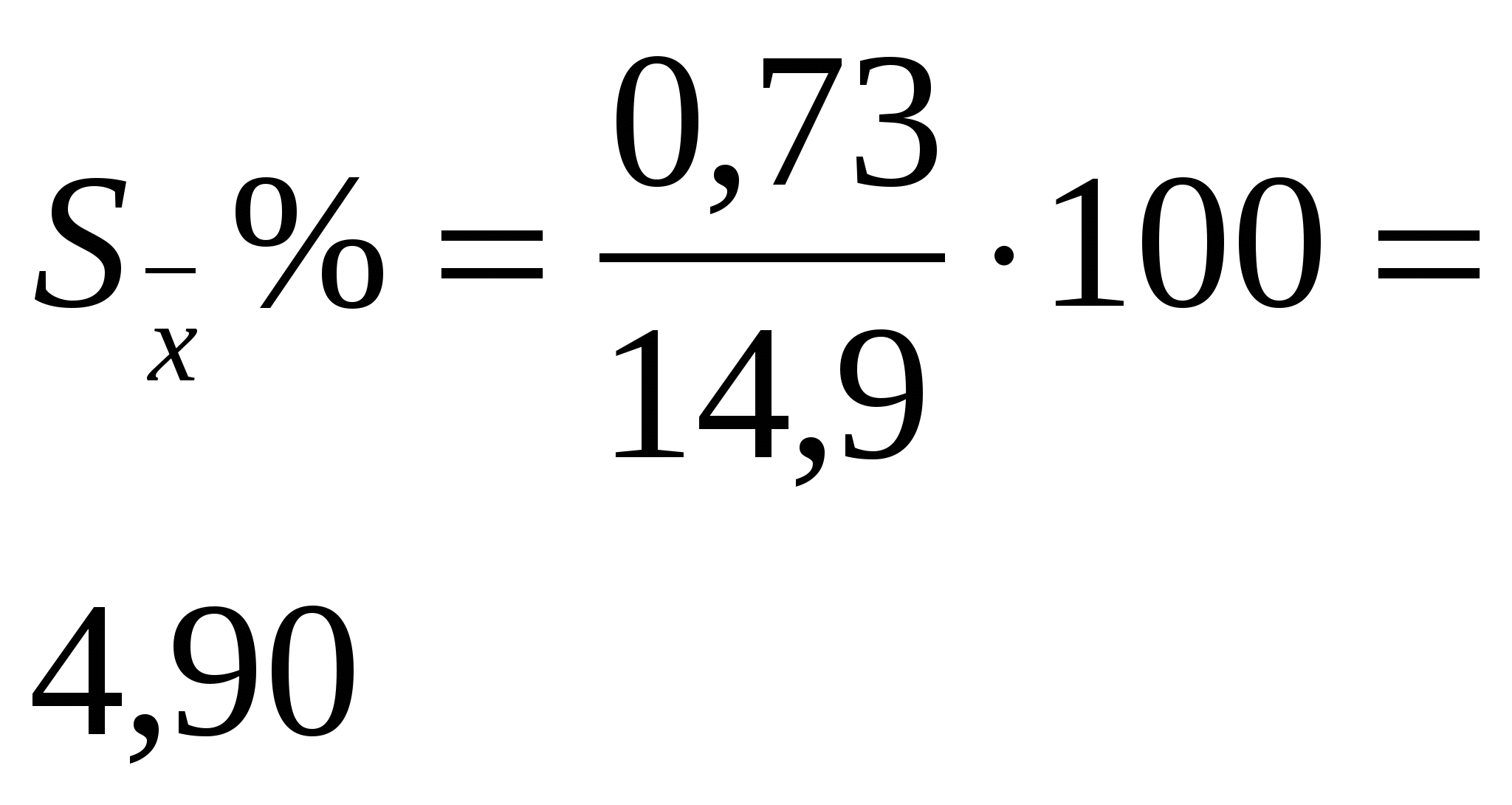Курс лекций по основам. Роль с Х. науки в развитии апк страны
 Скачать 1.33 Mb.
|
|
Тема: Дробный метод обработки данных Этот метод применяется для обработки результатов вегетационного опыта, в котором отсутствует связь между сравниваемыми вариантами – сосудами, а также полевых и лабораторных опытов, когда ошибки средних арифметических вычисляются на основании большого числа наблюдений (n = 20–30). Метод может в отдельных случаях применяться для обработки результатов полевого опыта (при отсутствии систематических ошибок). В опыте, проведённом по схеме: 1. Зяблевая вспашка на 20 – 22 см (контроль) 2. Осенняя плоскорезная обработка на 20 - 22 см 3. Осенняя плоскорезная обработка на 10 – 12 см 4. Весеннее лущение жнивья на 10 -12 см Получены следующие данные по урожайности: Обработку данных дробным методом проводят в следующей последовательности: 1.Составляют таблицу урожаев и вычисляют среднюю арифметическую величину по каждому варианту (  . 2. Находят отклонения поделяночных урожаев от среднего урожая по варианту (  – ). Правильность вычислений проверяют по равенству  (если найдена без остатка).3. Находят квадраты отклонений  и их суммы по каждому варианту в отдельности  4. Рассчитывают ошибки средних арифметических по вариантам.  5. Определяют разности между средними урожаями между контролем и опытными вариантами.  где d – разность;  и  – средние арифметическиесравниваемых вариантов 6. Определяют ошибку разности между двумя средними (контролем и опытным вариантом).  где Sd – ошибка разности и  – ошибки сравниваемых вариантов Обработка урожайных данных, полученных в опыте дробным методом
Эта формула применяется для расчёта  при условии, что  , и в случае, когда ошибки средних арифметических вычислены при большом числе наблюдений (n >20);7. Устанавливают существенность разности. Существенность различий между и оценивают по отношению их разности ( ) к её ошибке Sd. Это отношение и называется критерием существенности разности или критерием Стьютента ( tфакт ).По экспериментальным данным вычисляем фактическое значение критерия (  ): = Величина критерия t – показывает, во сколько раз разность (d) больше ошибки разности (Sd) Значение tтеор.- находят в приложении рабочей тетради при 5% или 1% уровне значимости и числе степеней свободы υ = n1 + n2 – 2 В нашем примере при Р = 5% и υ = 4 + 4 – 2 = 6 tтеор = 2,4 Разность считается существенной, если tфакт ≥ tтеор. При tфакт ≤ tтеор. разность между средними не выходит за пределы случайных колебаний т.е. считается несущественной. Так в нашем примере разница между вариантом с осенней плоскорезной обработкой на 20-22 см и вариантом с осенней вспашкой на 20-22 см в 2,0 ц/га будет существенной, т.к.  . Разница между вариантом с осенней плоскорезной обработкой на 10-12 см и контролем также существенна ( =4,6 > =2,4). Четвёртый вариант (без осенней обработки) не дал существенной прибавки урожая по сравнению с контролем.При достаточно большом числе наблюдений (  >20-30) разность  обычно считается существенной при уровне значимости 5%, если ≥ 2, а при уровне значимости 1% при ≥ 3. Если <2, то разность между средними считается несущественной.Несмотря на свою простоту, дробный метод имеет некоторые недостатки: - для оценки существенности разности используется отвлечённые показатели ( и ),- для каждого варианта в отдельности рассчитываются ошибка выборочной средней и ошибка разности, что увеличивает расчёты. ЛЕКЦИЯ № 7 ТЕМА: ДИСПЕРСИОННЫЙ АНАЛИЗ И ЕГО СУЩНОСТЬ Дисперсионный анализ считается наиболее совершенным методом. Он более других методов подходит для обработки данных полевых опытов, широко применяется в географической сети опытов по агротехнике с.- х. культур, , с удобрениями и в сортоиспытании. Этот анализ по сравнению с дробным и другими методами даёт возможность установить влияние всего комплекса факторов (изучаемых приёмов, плодородия почвы, случайных ошибок) и степень влияния каждого фактора в отдельности на изменчивость изучаемого признака (урожая в полевом опыте). Сущность дисперсионного анализа заключается в разложении общей вариации (общей суммы квадратов отклонений) и общего числа степени свободы на отдельные компоненты или структурные элементы эксперимента с целью оценки существенности действия (взаимодействия) изучаемых факторов по F-критерию. Фактическое значение этого критерия получают из отношения дисперсий изучаемого и неизучаемого факторов (  ). Стандартные значения критерия берут в соответствии с принятым уровнем значимости и числом степеней свободы для дисперсий числителя и знаменателя.Изменчивость изучаемого признака, обусловленную действием всех факторов, называют общим варьированием (или общей дисперсией) поделяночных урожаев. Общее варьирование выражается суммой квадратов отклонений поделяночных урожаев Х от среднего урожая опыта о, т.е.  . В зависимости от характера и методики опыта общее варьирование расчленяется на две-три или большее число составных частей:- варьирование между вариантами  , обусловленное действием изучаемых факторов (особенностями вариантов);- варьирование между повторениями  , вызванное различием в плодородии почвы по повторениям;- случайное (остаточное) варьирование  , являющееся следствием действия случайных ошибок в опыте, не контролируемых исследователем.При дисперсионном анализе одновременно обрабатывают данные нескольких вариантов (5-10 Общее варьирование опытных данных обусловлено влиянием изучаемых факторов (особенностями вариантов), различием в плодородии почвы отдельных повторений и действием случайных ошибок в опыте:  Из общего варьирования  можно вычленить варьирование, обусловленное влиянием изучаемых факторов , различием в плодородии почвы и выявить случайное варьирование , характеризующее ошибки опыта, от которых зависит его точность: При дисперсионном анализе можно использовать несколько методов (моделей) расчёта сумм квадратов отклонений для разных видов варьирования: от средней по опыту о; от произвольного начала (А); по фактическим данным (от фактического нуля, А=О).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- сумма урожаев
