КР надежность. Контрольная работа. Ростовский государственный университет путей сообщения (фгбоу во ргупс)

• Название: Ростовский государственный университет путей сообщения (фгбоу во ргупс)
• Анкор: КР надежность
• Дата: 03.02.2022
• Размер: 193.53 Kb.
• Имя файла: Контрольная работа.docx
• Тип: Контрольная работа; #350813

РОСЖЕЛДОР

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВО РГУПС)

Факультет – Заочный

Кафедра «Автоматизированные системы электроснабжения»

Специальность: 23.05.05 – Системы обеспечения движения поездов

Специализация №1 – Электроснабжение железных дорог

Контрольная работа

по дисциплине:

«Надежность систем электроснабжения»

Вариант № 5
Студент группы

ЭЖС-5-710 _______________Иванская Д.А.
Дата ______________

к. т. н., доцент _______________ Семенов Ю.Г.

2022

Введение
Сложные технические объекты (системы), рассчитанные на длительный срок службы, создаются, как правило, ремонтируемыми. Переход системы из неработоспособного (предельного) состояния в работоспособное осуществляется с помощью операций восстановления или ремонта. К первым, в основном, относятся операции идентификации отказа (определение его места и характера), замены, регулирования, заключительных операций контроля работоспособности системы в целом. Переход системы из предельного состояния в работоспособное осуществляется с помощью ремонта, при котором происходит восстановление ресурса системы в целом.

Цель контрольной работы.

Приобретение навыков по расчету показателей надежности резервированных систем, восстанавливаемых путем ремонта в эксплуатации.

Решаемые задачи.

В контрольной работе решаются следующие задачи:

1. Задача по определению коэффициентов готовности и вынужденного простоя нерезервированной восстанавливаемой системы, содержащей только один рабочий элемент [1]. Для определения условий вероятности состояний системы составляется системы дифференциальных уравнений.

2. Задача по определению коэффициентов готовности и вынужденного простоя резервированной восстанавливаемой системы, содержащей один рабочий и один резервный элемент [1]. В задаче используется вариант с общим резервированием замещением либо вариант с общим резервированием и постоянно включенным резервом (по заданию). Для определения условий вероятности состояний системы составляется системы дифференциальных уравнений.

3. Производится сравнение эффективности резервирования путем сравнения функций надежности систем без резервирования и с резервированием, а также своевременности и сроков ремонта.

Исходные данные: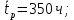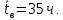




Задача №1
Решение:

Нерезервированная восстанавливаемая система в произвольный момент времени находится в одном из двух состояний: работоспособном 0 или неработоспособном 1. Процесс ее функционирования можно отразить графом состояний: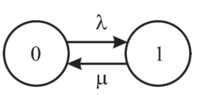



Рисунок 1. Граф состояний нерезервированной системы
Из состояния 0 в состояние 1 система переходит в результате отказов с интенсивностью 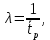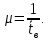, а из 1 в 0 - в результате восстановления с интенсивностью . В дальнейшем будем считать, что потоки отказов и восстановлений являются простейшими: , . Это значит, что производительность труда ремонтника постоянна и не зависит от времени.





Найдем 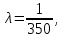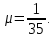и поставив исходные данные:





Основным показателем надежности нерезервированной восстанавливаемой системы является коэффициент готовности Г(t). Сокращение времени восстановления ведет к увеличению коэффициента готовности и не влияет на безотказность системы. Рассмотрим работу системы на интервале времени t= 0….2000 ч. Обозначим через P₀(t), P₀(t +∆t) и P₁(t), P₁(t +∆t) - вероятности того, что в момент времени t и t +∆t система находится в состоянии 0 и 1. Тогда P₀(t) + P₁(t) = 1 и Г(t) = P₀(t). Обозначим также через и - условную вероятность того, что в момент времени t система находится или в состоянии 0 или в состоянии 1, а в момент времени t +∆t или в состоянии 1 или в состоянии 0, т.е. за интервал времени ∆t произошел отказ (восстановление) системы.

Будем считать, что за время может 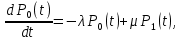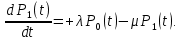произойти только один отказ или только одно восстановление.

Тогда:





Решение системы при начальных условиях P₀(t) = 1 и P₁(t) = 0, т.е. в начальный момент времени система работоспособна, имеет вид: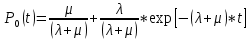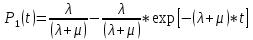





Найдем значение P₀(t) на интервале времени t= 0….2000 ч:

P₀(0) = 1;

P₀(100) = 0,913014483;

P₀(200) = 0,909260248;

P₀(300) = 0,909098218;

P₀(400) = 0,909091225;

P₀(500) = 0,909090923;

P₀(600) = 0,90909091;

P₀(700) = 0,909090909;

P₀(800) = 0,909090909;

P₀(900) = 0,909090909;

P₀(1000) = 0,909090909;

P₀(1100) = 0,909090909;

P₀(1200) = 0,909090909;

P₀(1300) = 0,909090909;

P₀(1400) = 0,909090909;

P₀(1500) = 0,909090909;

P₀(1600) = 0,909090909;

P₀(1700) = 0,909090909;

P₀(1800) = 0,909090909;

P₀(1900) = 0,909090909;

P₀(2000) = 0,909090909.

Найдем значение P₁(t) на интервале времени t= 0….2000 ч:

P₁(0) = 0;

P₁(100) = 0,08698551734;

P₁(200) = 0,0907397634;

P₁(300) = 0,0909017824;

P₁(400) = 0,0909087755;

P₁(500) = 0,090909091;

P₁(600) = 0,090909077;

P₁(700) = 0,090909091;

P₁(800) = 0,090909091;

P₁(900) = 0,090909091;

P₁(1000) = 0,090909091;

P₁(1100) = 0,090909091;

P₁(1200) = 0,090909091;

P₁(1300) = 0,090909091;

P₁(1400) = 0,090909091;

P₁(1500) = 0,090909091;

P₁(1600) = 0,090909091;

P₁(1700) = 0,090909091;

P₁(1800) = 0,090909091;

P₁(1900) = 0,090909091;

P₁(2000) = 0,090909091.

Функция готовности определяет вероятность нахождения системы в работоспособном состоянии в момент t, совпадает с вероятностью работоспособного состояния, т.е. Г(t) = Р₀(t). График функции готовности Г(t) для заданной системы без резервирования представлен на рисунке 2.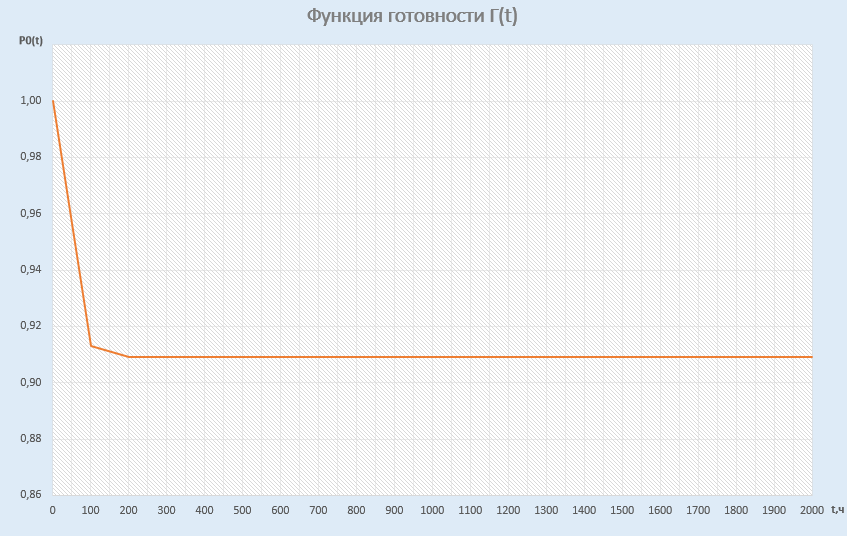


Рисунок 2. График функции готовности системы Г(t) без резервирования
Это означает, что при экспоненциальных законах распределения времени наработки на отказ и времени восстановления, случайный процесс работы восстанавливаемой системы стабилизируется, и вероятность застать систему работоспособной в произвольный момент времени остается постоянной. Система с указанным свойством называется эргодической, а сам процесс - Марковским случайным процессом. Случайный процесс называется Марковским, если для любого момента времени вероятности всех состояний системы в будущем зависят только от ее состояния в настоящем и не зависят от того, когда и как система пришла в это состояние.

Задача №2
Решение:

Дублированная система может находиться в одном из трех состояний, которые обозначим цифрами: 0 - система работоспособна (оба элемента работоспособны); 1 - система работоспособна, но один из элементов отказал (система предрасположена к отказу); 2 - система неработоспособна (отказала).

Обозначим вероятности перечисленных выше состояний через P₀(t), P₁(t), P₂(t). Эти вероятности зависят от начальных состояний системы, в которых она находилась при t=0.

Граф состояний дублированной системы с нагруженным резервом представлен на рисунке 3.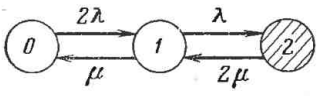


Рисунок 3. Граф состояний дублированной системы с нагруженным резервом
Процесс функционирования рассматриваемой восстанавливаемой резервированной системы можно определить, как нагруженный резерв; при отказах элементов они могут ремонтироваться как по одному, так и одновременно (восстановление без ограничений).

При нахождении в состояниях 0 и 1 система работоспособна, в состоянии 2 - неработоспособна.

Система дифференциальных уравнений для этой системы имеет вид: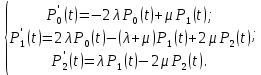



Решим полученную систему при начальных условиях Р₀(0) = 1, P₁(0) = Р₂(0) = 0 и найдем зависимость Р_i (t) для i=0, 1, 2.

Для рассматриваемой системы функция готовности имеет вид:

Г(t) = Р₀(t) + P₁(t) = 1- Р₂(t).

Функция готовности для рассматриваемой резервированной системы с восстановлением имеет вид: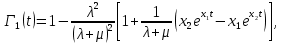



где , .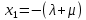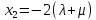

Найдем значение Г₁ (t) на интервале времени t= 0….2000 ч:

Г₁(0) = 1;

Г₁(100) = 0,99244843;

Г₁(200) = 0,991766325;

Г₁(300) = 0,991736866;

Г₁(400) = 0,991735595;

Г₁(500) = 0,99173554;

Г₁(600) = 0,991735537;

Г₁(700) = 0,991735537;

Г₁(800) = 0,991735537;

Г₁(900) = 0,991735537;

Г₁(1000) = 0,991735537;

Г₁(1100) = 0,991735537;

Г₁(1200) = 0,991735537;

Г₁(1300) = 0,991735537;

Г₁(1400) = 0,991735537;

Г₁(1500) = 0,991735537;

Г₁(1600) = 0,991735537;

Г₁(1700) = 0,991735537;

Г₁(1800) = 0,991735537;

Г₁(1900) = 0,991735537;

Г₁(2000) = 0,991735537.

Зависимость функции готовности для рассматриваемой резервированной системы с восстановлением представлена на рисунке 4.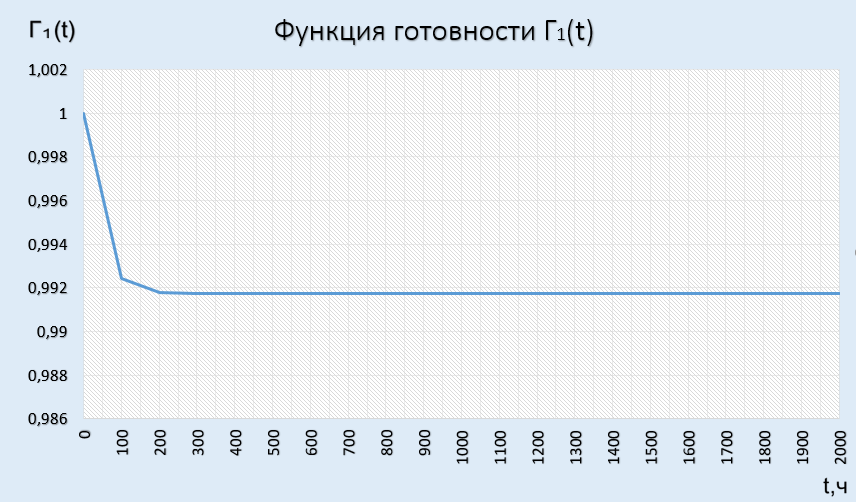


Рисунок 4. График функции готовности системы Г(t) резервированной системы с восстановлением
Таким образом, для повышения готовности восстанавливаемой дублированной системы необходимо стремиться к созданию условий, обеспечивающих осуществление ненагруженного резерва и восстановления без ограничений.

Анализ результатов и выводы
На рисунке 5 представлена функция готовности для нерезервированной восстанавливаемой системы (синяя линия) и резервированной восстанавливаемой системы (оранжевая линия) на интервале времени t = 0…..2000 ч с одинаковыми исходными .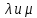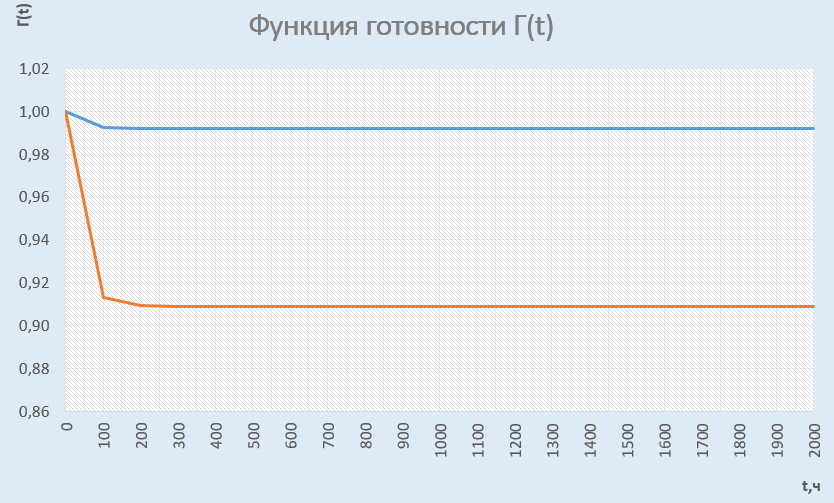




Рисунок 5. Функция готовности
Из графика видно, что введение резервирования в восстанавливаемую систему дает существенное приращение надежности системы при относительно невысокой надежности основной цепи.
Список использованных источников
1. Основы теории надежности и технической диагностики. Методическое пособие к лабораторно-практическим работам / Ю.Г. Семенов; Рост. гос. ун-т путей сообщения. Ростов н/Д, 2011. – 66 с.

2. Дружинин Г. В. Надежность автоматизированных производственных систем. - 4-е изд., перераб. и доп. – М.: Энергоиздат, 1986. – 480 с.

3. Ефимов А.В. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж.-д. трансп. / Ефимов А.В., Галкин А.Г. – Москва: УМПК МПС России, 2000. – 512 с.