Интегральные уравнения Вольтерры 2-го порядка. Курсова_робота_Олійник_Дар'ї. Розвязування інтегральних рівнянь Вольтерра другого роду
 Скачать 31.53 Kb. Скачать 31.53 Kb.
|
|
Дніпровський національний університет імЕНІ Олеся Гончара ФАКУЛЬТЕТ ПРИКЛАДНОЇ МАТЕМАТИКИ КАФЕДРА ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ ТАМАТЕМАТИЧНОЇ КІБЕРНЕТИКИКУРСОВА РОБОТА з основ прикладної математики на тему « Розв’язування інтегральних рівнянь Вольтерра другого роду » Виконав: студент групи ПА–17–1 спеціальності 113 «Прикладна математика» Олійник Дар’я Ігорівна Керівник: доцент кафедри ОМ та МК Волошко Віктор Леонідович Кількість балів____________ Національна шкала ________ Члени комісії : ___________ ____Козакова Н.Л.___ (підпис) (прізвище та ініціали) ___________ _Тонкошкур І.С.___ (підпис) (прізвище та ініціали) ___________ _Черницька О.В.___ (підпис) (прізвище та ініціали) м. Дніпро 2020 РЕФЕРАТ Курсова робота: 35 с., 6 рис., 9 джерел, 1 додаток. Об'єкт дослідження: чисельні та точні методи розв’язання інтегральних рівнянь Вольтерра другого роду. Мета роботи: вивчення існуючих чисельних методів розв’язання інтегральних рівнянь Вольтерра другого роду за допомогою розв’язання частинних похідних та порівняння їх з аналітичними методами. Одержані висновки та їх новизна: проаналізовано різні чисельні методи для розв’язання інтегральних рівнянь Вольтерра другого роду, та написано програму з використанням математичного пакету, яка розв’язує інтегральні рівняння. Результати досліджень можуть бути застосовані при вивченні фізичних явищ, таких як коливання струни, мембран тощо. Перелік ключових слів: РІВНЯННЯ ВОЛЬТЕРРА ДРУГОГО РОДУ, ЧИСЕЛЬНІ МЕТОДИ, МЕТОД КВАДРАТУР ЗМІСТ ВСТУП 1 ПОСТАНОВКА ЗАДАЧІ (Основні поняття про інтегральні рівняння та їх класифікація.) 2 ІСНУВАННЯ ТА ЄДИНІСТЬ РОЗВ’ЯЗКУ ІНТЕГРАЛЬНОГО РІВНЯННЯ ВОЛЬТЕРРА ДРУГОГО РОДУ 3 АНАЛІТИЧНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ІНТЕГРАЛЬНИХ РІВНЯНЬ ВОЛЬТЕРРА ДРУГОГО РОДУ 4 НАБЛИЖЕНЕ РОЗВ’ЯЗУВАННЯ ІНТЕГРАЛЬНОГО РІВНЯННЯ ВОЛЬТЕРРА ДРУГОГО РОДУ 5 Програмна реалізація алгоритму 6 Приклади чисельної реалізації ВСТУП Випадки формулювання задач у вигляді інтегральних рівнянь зустрічалися вже у першій половині XIX ст. Прикладами можуть бути формули обернення Фур’є і рівняння Абеля, яке отримано у ході розв’язку задачі таутохроні. Інтегральні рівняння привернули до себе увагу математиків на рубежі XIX-XX ст. Зараз існує визначений і достатньо широкий круг задач, для математичного опису якого використовують інтегральні рівняння і перетворення. Вони знайшли ефективне застосування у: фізиці – задачі дифузії і явище переносу, теорія потенціалу, теорія пружності, теплопровідність тощо, механіці – багатомасові системи, коливання валів й інші задачі аналізу динаміки машин і механізмів, аеродинаміці – власні коливання крил самолету, флатер тощо, електротехниці – аналіз і оптимальний синтез електричних ланцюгів тощо. Треба підкреслити важливу роль інтегральних рівнянь у розв’язку граничних задач і аналізів випадкових процесів. Рівняння, в яких шукана функція міститься під знаком інтегралу і поза, називають інтегральним рівняння другого роду. Якщо межі інтегрування фіксовані, то інтегральне рівняння називаються рівнянням Фредгольма, а якщо межі інтегрування змінні, то – рівняння Вольтерра. Деякі з задач приводять до інтегральних рівнянь. До них можна віднести задачі: про відновлення функції 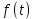 за її перетворення Фур’є, Коші для звичайного диференціального рівняння першого порядку, початкові для лінійних диференціальних рівнянь, Абеля, про малі коливання струни. за її перетворення Фур’є, Коші для звичайного диференціального рівняння першого порядку, початкові для лінійних диференціальних рівнянь, Абеля, про малі коливання струни.ПОСТАНОВКА ЗАДАЧІ Інтегральне рівняння – це рівняння, яке містить невідому функцію під знаком інтеграла, наприклад, 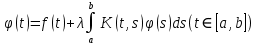 (1. 0) (1. 0)або 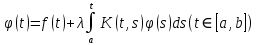 (1. 2) (1. 2)де 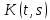 і і 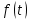 – задані функції, а – задані функції, а 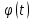 – шукана. Функція – шукана. Функція 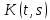 – ядро інтегрального рівняння, а – ядро інтегрального рівняння, а 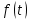 – вільний член, – вільний член, 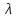 – параметр (з ℝ або ℂ). Якщо (1.1) ядро – параметр (з ℝ або ℂ). Якщо (1.1) ядро 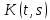 визначене в квадраті визначене в квадраті 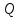 : :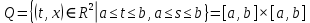 (1.3) (1.3)а якщо (1.2) – в трикутнику 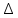 : :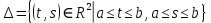 (1.4) (1.4)Ці рівняння належать до класу лінійних інтегральних рівнянь, де шукана функція 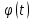 входить у ці рівняння лінійно. входить у ці рівняння лінійно. Коли шукана функція міститься лише під знаком інтеграла, то рівняння називають інтегральним рівняння першого роду. 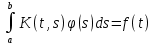 (1.5) (1.5)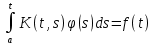 (1.6) (1.6)Рівняння, в яких функція міститься і під знаком ітеграла, і поза, називають інтегральними рівняннями другого роду. Наприклад, рівняння (1.1) і (1.2) Рівняння Фредгольма – межі інтегрування фіксовані (1.1), (1.5), рівняння Вольтерра – межі інтегрування змінні (1.2), (1.6). (1.1), (1.2), (1.5), (1.6) називають однорідними рівняннями 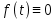 , а в протилежному випадку – неоднорідними. , а в протилежному випадку – неоднорідними.Ядро 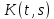 і вільний член і вільний член 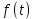 є неперервними функціями або задовольняють умовам інтегрованості є неперервними функціями або задовольняють умовам інтегрованості 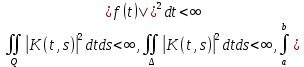 До розгляду допускаються комплексні функції. Функція 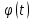 є розв’язком інтегрального рівняння і перетворює його на тотожність по є розв’язком інтегрального рівняння і перетворює його на тотожність по 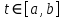 . .Наведемо приклади інтегральних рівннянь різних типів та їх розв’язки:  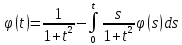 Показати, що 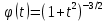 э розв’язком рівняння. э розв’язком рівняння.Розв’язок: підставимо замість 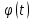 у праву частину рівняння функцію у праву частину рівняння функцію 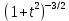 , отримаємо: , отримаємо: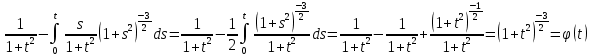 Отже, відовідно до визначення, 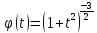 є розв’язком рівняння. є розв’язком рівняння.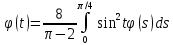 Показати, що 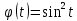 э розв’язком рівняння. э розв’язком рівняння.Розв’язок: підставимо замість 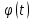 у праву частину рівняння функцію у праву частину рівняння функцію 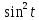 , отримаємо: , отримаємо: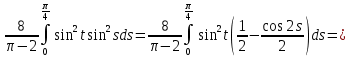 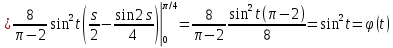 Отже, відовідно до визначення, 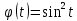 є розв’язком рівняння. є розв’язком рівняння.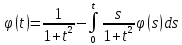 Показати, що 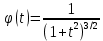 э розв’язком рівняння. э розв’язком рівняння.Розв’язок: підставимо замість 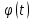 у праву частину рівняння функцію у праву частину рівняння функцію 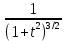 , отримаємо: , отримаємо: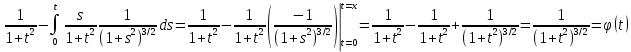 Отже, відовідно до визначення, 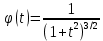 є розв’язком рівняння. є розв’язком рівняння.Розв’язання задачі для лінійних диференціальних рівнянь приводить до лінійних рівнянь Вольтерра другого роду. Нехай, наприклад, маємо диференціальне рівняння другого порядку 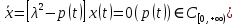 (0. 0) (0. 0) і початкові умови 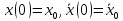 . Розглянувши неоднорідне рівняння . Розглянувши неоднорідне рівняння  з тими самими початковими умовами, де з тими самими початковими умовами, де 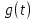 – деяка неперервна функція, за методом Лагранжа знайдемо – деяка неперервна функція, за методом Лагранжа знайдемо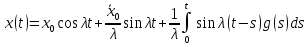 Повертаючись до рівняння (0.1), в якому 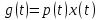 , дістанемо , дістанемо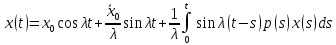 Це інтегральне рівняння Вольтерра другого роду відносно 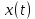 : :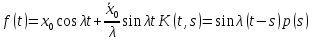 Розглянемо загальний випадок і застосуємо інший метод. Нехай маємо задачу Коші 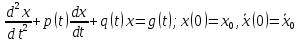 де функції 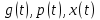 неперервні, наприклад, при неперервні, наприклад, при 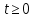 . .Покладемо 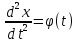 . Беручи до уваги початкові умови і формулу . Беручи до уваги початкові умови і формулу 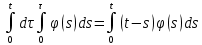 , знаходимо , знаходимо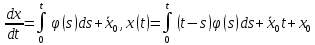 Підставимо тепер вирази для 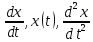 у диференціальне рівняння. Відносно у диференціальне рівняння. Відносно 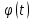 дістанемо дістанемо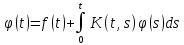 де 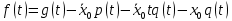 , ,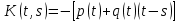 . Це інтегральне рівняння Вольтерра другого роду. Якщо функцію . Це інтегральне рівняння Вольтерра другого роду. Якщо функцію 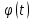 знайдено з цього рівняння, то знайдено з цього рівняння, то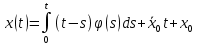 . . |
