Практическое руководство-ФинМат. Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1

• Название: Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1
• Дата: 10.02.2018
• Размер: 1.16 Mb.
• Имя файла: Практическое руководство-ФинМат.doc
• Тип: Руководство; #36180
• страница: 14 из 14

Задание 2.3

Кредит в размере 30000 д.е. выдан на срок 3 года и 160 дней при начислении сложных процентов по годовой процентной ставке 0,065 с временной базой 365 дней. Определите величину долга к концу сро­А.

Решение.

В практике финансовых вычислений расчет наращенной суммы для данного случая комбинируют: наращенную сумму для целого числа периодов рассчитывают по принципу сложных процентов , для дробного числа – по принципу простых процентов :

, где Р – первоначальная сумма долга, j – годовая процентная ставка, l – число лет,  - неполное число дней в периоде.

Находим:



Таким образом величина долга к концу срока составит 37270 д.е.

Задание 3.6

Выразить в форме y = a∙e^kt следующие функции : y = 2^t ; y = 1000∙2^t/3 ; y = 5∙(1,04)^t ; y = 6∙10⁸∙(1,05)^-t.

Решение.

Находим для функции y = 2^t:

Логарифмируем правые и левые части заданной функции , а затем преобразовываем функцию к требуемому виду lny = ln2^t  lny = t∙ln2 y = e^t∙ln2 y = e^ln2∙e^t y = 2∙e^t

В результате получим y = 2∙e^t.

Находим для функции y = 1000∙2^t/3:

Ln(y/1000) = ln2^t/3  ln(y/1000) = (t/3)∙ln2 y/1000 = e ^(t/3)∙ln2 y/1000 = e^ln2∙e^t/3

y = 2000∙e^t/3

В результате получим y = 2000∙e^t/3.

Аналогично находим и для остальных функций.

y = 5∙(1,04)^t у = 5∙1,04∙e^t  y = 5,2∙e^t

y = 6∙10⁸∙(1,05)^-t  y = 6∙10⁸∙1,05∙e^t  y = 6,3∙10⁸∙e^t.

Задание 4.9

Найдите годовую номинальную процентную ставку, соответствующую эффективной процентной ставке 0,084, если сложные проценты начисляются один раз: а) в полугодие; б) в квартал; в) в месяц; г) непрерывно.

Решение.

Для сравнения доходов от использования той или иной схемы начисления процентов применяется эффективная процентная ставка , начисление сложных процентов за год по которой дает то же соотношение между S(0) и S(t), что и при любой другой схеме начисления процентов.



Если в контракте указаны эффективная процентная ставка i_эф и число начислений m сложных процентов , то можно найти номинальную ставку по формуле:



а) для полугодового начисления процентов находим: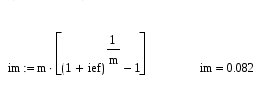



при полугодовом начислении процентов номинальная ставка составит 0,082;

б) для квартального начисления процентов: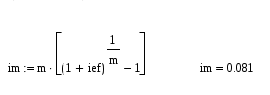



при поквартальном начислении процентов номинальная ставка составит 0,081;

в) для ежемесячного начисления процентов: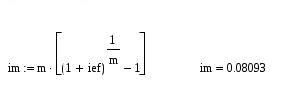



при ежемесячном начислении процентов номинальная ставка составит 0,08093;

г) при непрерывном начислении процентов:

воспользуемся соотношением ;

в нашем случае t = 1 , поэтому ,

при непрерывном начислении процентов номинальная ставка составит 0,084.

Задание 5.12

Сертификат номиналом 100 тыс. руб. с объявленной доходностью 12 % годовых, начисляемых простыми процентами, и сроком на 720 дней куплен по цене 110 тыс. руб. за 250 дней до погашения. Определите доходность инвестиций в виде эффективной процентной ставки.

Решение.

По формуле простых процентов определим стоимость сертификата на момент погашения.

, где j – годовая (номинальная) ставка ; n = 720/260 = 2 года- продолжительность периода .

S=100·(1+0.12·2)=124 тыс. р.

Тогда доходность операции: d = S/P₁ – 1 = 124/110 – 1 = 0,127 или 12,7%, где Р₁ – покупная цена сертификата.

Определи эффективную процентную ставку операции:

i_эф = (d∙m)/360 = ( 0,127∙250)/360 = 0,088 или 8,8%, где m – число дней операции.

Эффективная процентная ставка операции составляет 8,8%.

Задача 6.15

Молодожены имеют годовой доход 45000 д.е. Ипотечный банк дает в долг сумму, которая должна постоянно погашаться одной третьей месячного дохода. Бели банк использует начисление слож­ных процентов по месячной процентной ставке 0,012 и долг погаша­ется в течение 25 лет, то какова может быть величина взятого кредита?

Решение.

Определим величину ежемесячного платежа по кредиту:

R = 45000/(3∙12) = 1250 д.е.

Величину кредита определим по формуле: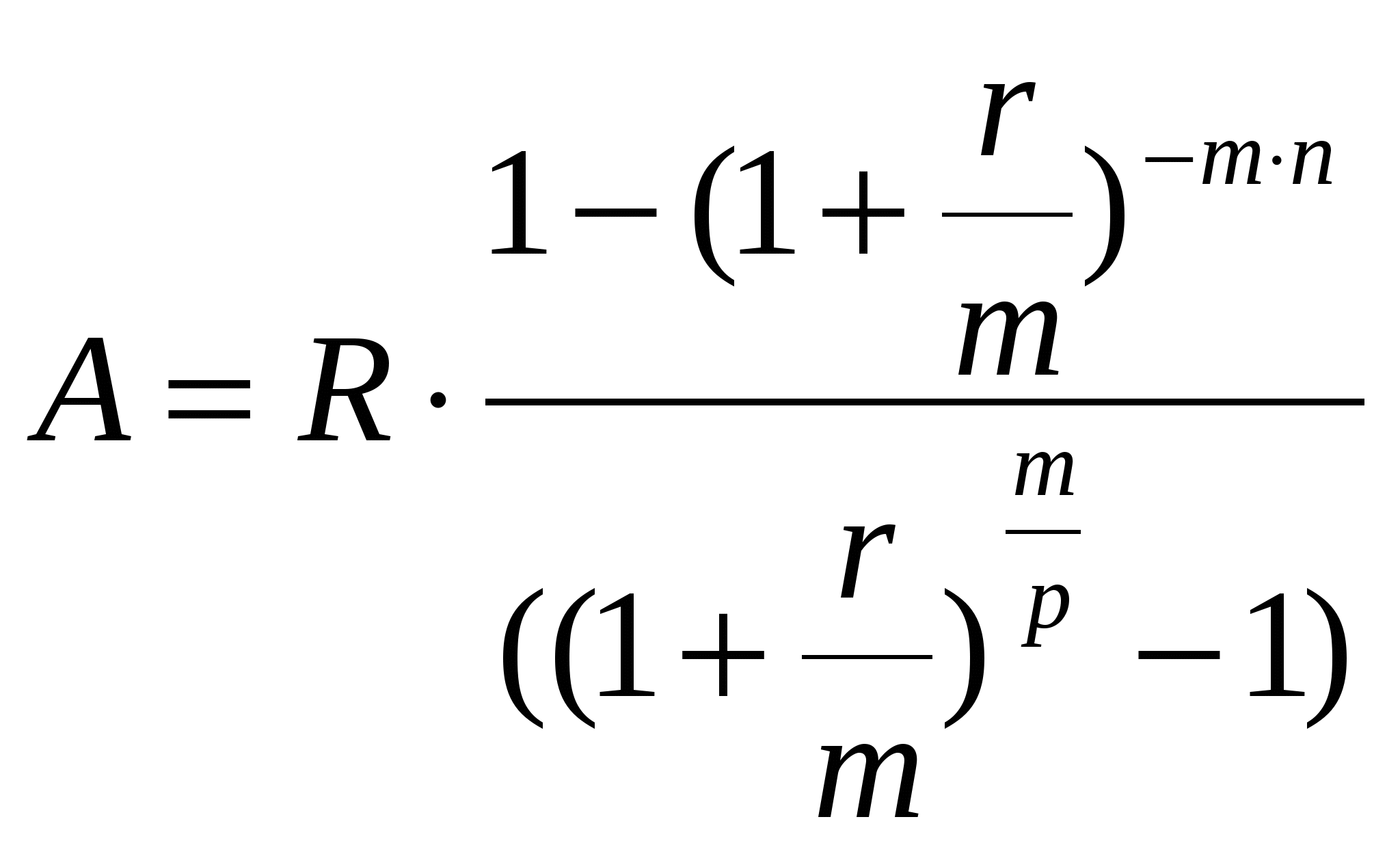

, где r- годовая процентная ставка ренты, р – число выплат в году, А - современная величина для n-срочной ренты , при начислении процентов m раз в год.

В нашем случае r = 0,012∙12 = 0,144, p = m =12, n = 25.

Находим: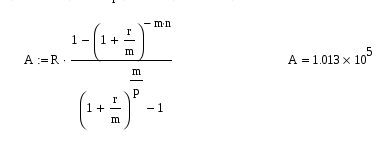



Семья может взять кредит в размере 101300 д.е.
Задача 7.18

Семья планирует купить новый автомобиль за 10000 д.е. Эту сумму семья взяла в долг на 36 месяцев под сложные проценты по процентной ставке 0,0075 в месяц. Определите величину ежемесяч­ных выплат.

Решение.

В данной задаче необходимо определить величину разового рентного платежа по современной величине ренты. Воспользуемся формулой: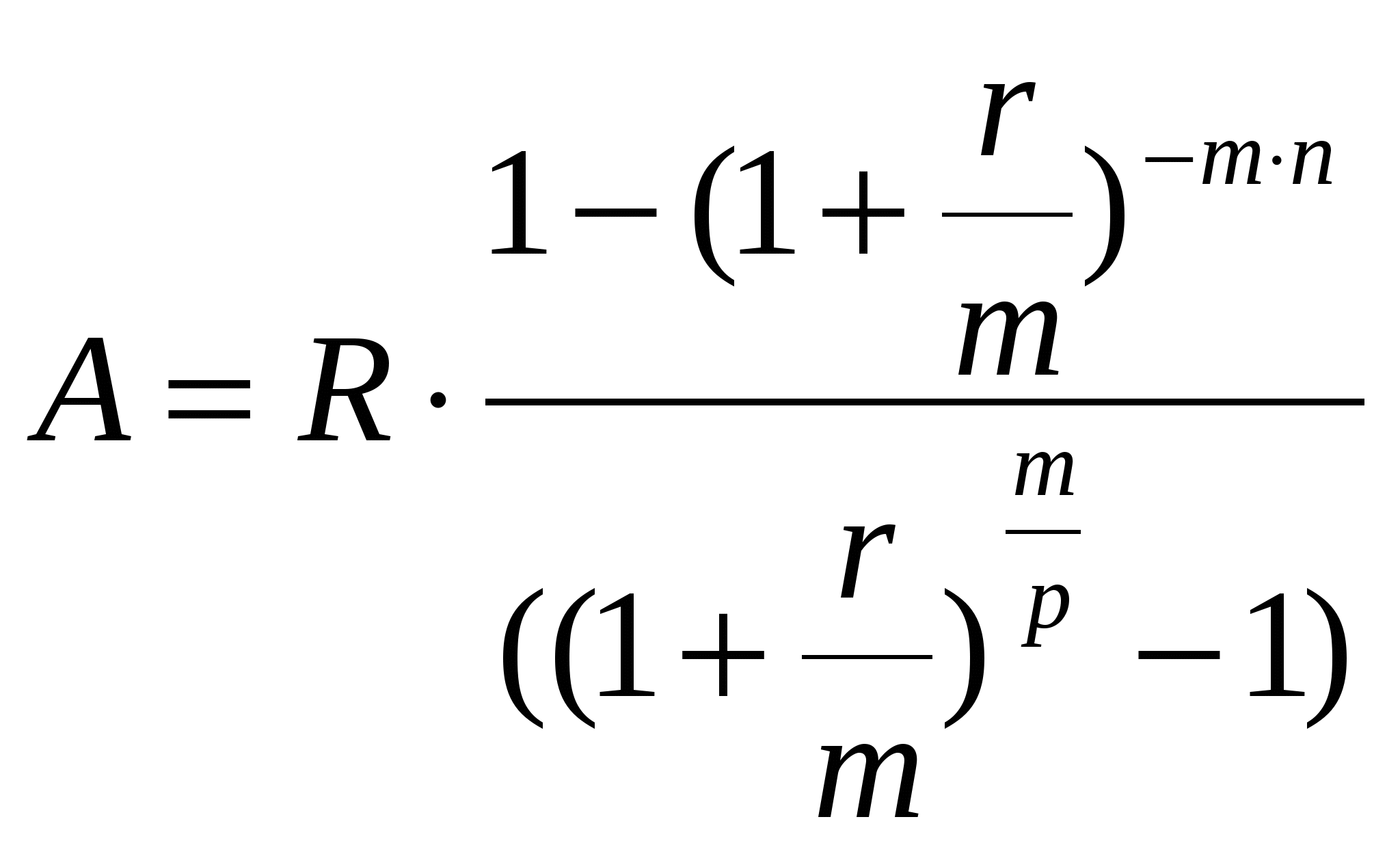

, где r- процентная ставка ренты , р – число выплат в году, А - современная величина для n-срочной ренты , при начислении процентов m раз в год :
Тогда разовый рентный платеж определяется как: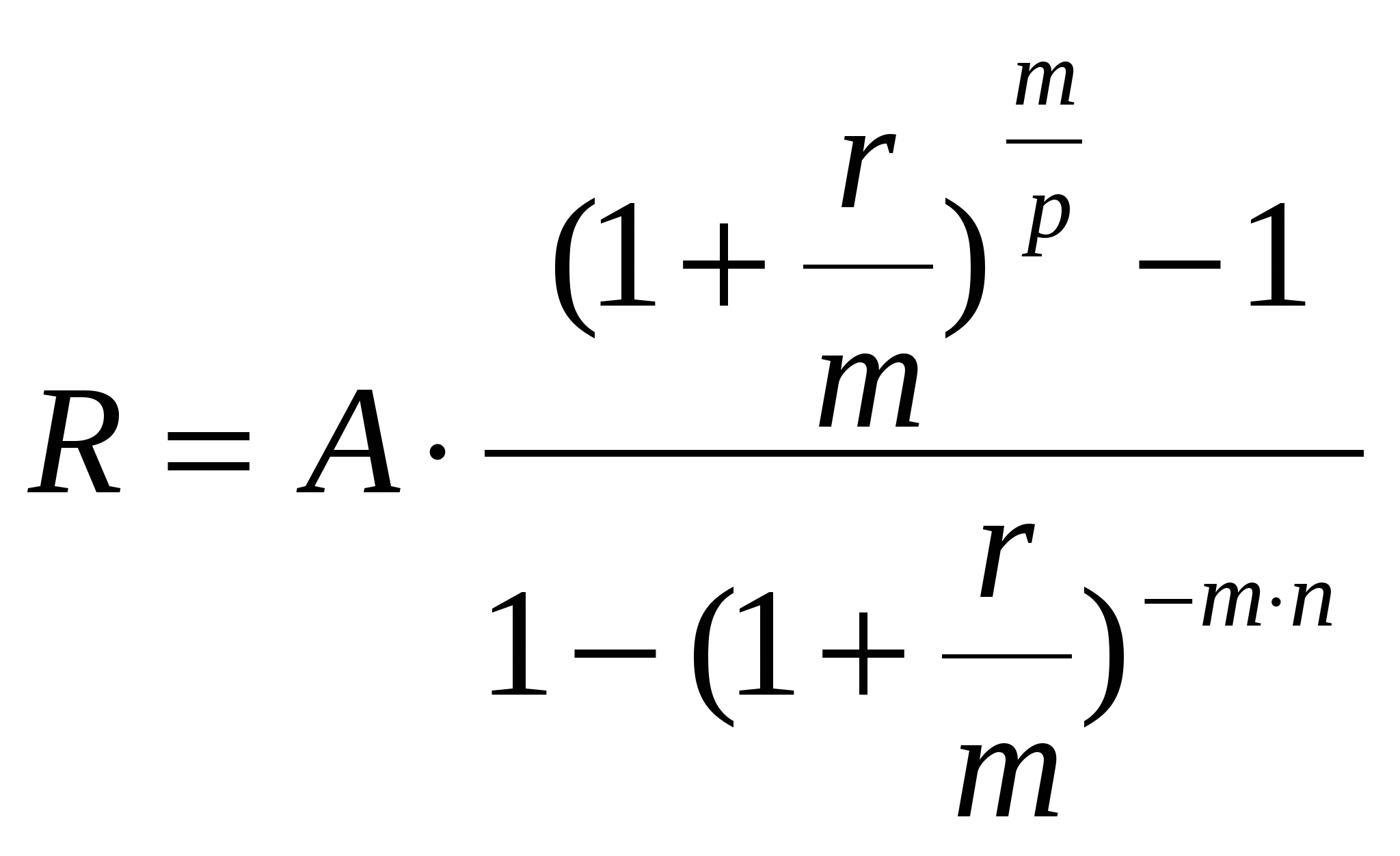



В нашем случае А= 10000д.е., n = 36/12 = 3, m = p = 12, r = 0,0075∙12 = 0,09.

Находим: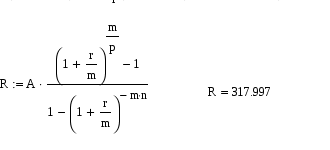



Ежемесячно семья должна выплачивать 317,997 д.е.

Задача 8.1

Пятилетний контракт предусматривает, что после первого пла­тежа 5000 д.е., производимого в конце первого года, последующие платежи ежегодно увеличиваются на 1000 д.е. При этом на платежи начисляются сложные проценты по годовой процентной ставке 0,08. Определите наращенную сумму потока платежей данного контракта, а также его современную величину.

Решение.

Современную стоимость данного потока платежей найдем как сумму дисконтированных платежей. Выберем момент времени на который будем производить дисконтирование t₀ = 0, тогда



27340 д.е.

Тогда наращенную сумму потока платежей определим как:

д.е.

Наращенная сумма потока платежей составит 40171,4 де.

Помощь на экзамене онлайн.