Практическое руководство-ФинМат. Руководство к практическим занятиям и самостоятельной работе по финансовой математике Содержание по финансовой математике 1
 Скачать 1.16 Mb.
|
Тема 12. Практическое приложение финансовых вычисленийРассмотрим практическое приложение финансовых вычислений на примере планирования погашения задолженности и ипотечных кредитов. На практике часто применяются способы погашения долга равными платежами или равными выплатами долга через равные промежутки времени. Каждый из способов имеет свои преимущества. При равных платежах заемщик до конца договора выплачивает одни и те же суммы, включающие в себя проценты и погашающие части долга, которые не равны между собой. При равных выплатах долга платежи не одинаковы, но легко определяются остатки долга. Цель проведения занятия –рассмотреть способы практических приложений финансовых вычислений, научиться выбирать оптимальную схему погашения задолженности и ипотечных кредитов, используя формулы финансовых вычислений и электронные таблицы EXCEL. Типовые задачи с решениями Пусть заем в сумме Р выдан под r простых ссудных процентов на n периодов. К концу финансовой операции величина займа составит величину  .Если предполагается возвращать займ одним платежом в конце срока финансовой операции, то величина F и есть размер возвращаемого платежа. Задача 1. Погашение займа одним платежом. Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить размер платежа, если ссуда возвращается одним платежом в конце срока финансовой операции и начисляются простые проценты. Решение Величину платежа находим по формуле при Р=5; r = 0,1; n =5: Размер платежа равен 7 500 000 руб. Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. К концу финансовой операции величина займа составит величину  .Если предполагается возвращать займ одним платежом в конце срока финансовой операции, то величина F и есть размер возвращаемого платежа. Задача 2. Погашение займа одним платежом. Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить размер платежа, если ссуда возвращается одним платежом в конце срока финансовой операции и начисляются сложные проценты. Решение Величину платежа находим по формуле при Р=5; r = 0,1; n =5: Размер платежа равен 8 052 550 руб. Сам заем называется основным долгом, а наращиваемый добавок –процентными деньгами. Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. За первый год процентные деньги составят величину rP. Если эти деньги выплатить, то останется только основной долг в размере Р. Таким же образом в конце каждого года (кроме последнего) выплачивается одна и та же величина rP. В конце n-ного, последнего года, выплаты составят величинуrP+Р, процентные деньги и сумму основного долга. Общая сумма выплат за n периодов составит величину Р+rPn=P(1+nr), т.е. операция погашения займа способом погашения основного долга одним платежом в конце эквивалентна наращению долга по схеме простых процентов по ставке r. Задача 3. Погашение основного долга одним платежом. Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить общую сумму выплат, если ссуда возвращается способом «погашение основного долга одним платежом в конце срока финансовой операции». Решение Величина процентных платежей за 8 лет составит rPn=0,155=2,5 Общая сумма выплат составит 2,5 млн.+ 5 млн. =7,5 млн.руб. Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. При погашении основного долга равными годовыми выплатами в конце каждого года выплачивается n-ная доля основного долга и проценты, начисленные на сумму долга, которой пользовались в течение года. В конце первого года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы Р, которой пользовались в течение года, равные величине rP. Общий платеж в конце первого года равен величине P/n+ rP. В конце второго года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы (Р- P/n), которой пользовались в течение года, равные величине r (Р- P/n). Общий платеж в конце второго года равен величине P/n+ r (Р- P/n). В общем случае в конце года k+1 общий платеж равен величине P/n+ r (Р- kP/n). Платежи каждого года образуют арифметическую прогрессию с разностью d=rP/n, первым членом a1 =P/n+ rPи последним членом an=P/n+ rP/n. Сумма n членов арифметической прогрессии равна 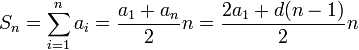 Величина выплат составит  Задача 4. Погашение основного долга равными годовыми выплатами Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить ежегодные выплаты и общую сумму выплат, если ссуда возвращается способом «погашение основного долга равными годовыми выплатами». Решение Найдем сумму арифметической прогрессии при Р=5000; r=0,1; n=5:5000+5000∙0.1(1+5) / 2=6500 Сумма ежегодных выплат представлена в таблице.
Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. При погашении займа равными годовыми выплатами ежегодные платежи можно рассматривать как годовую ренту (аннуитет) с продолжительностью nпериодов и неизвестным платежом, равным А. Неизвестный платеж ренты можно найти, приравнивая современную стоимость этой ренты сумме займа. Тогда платеж А находим из уравнения:  , поэтому  Общая сумма выплат при этом составит величину nA Задача 5. Погашение займа равными годовыми выплатами Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить общую сумму выплат, если ссуда возвращается способом «погашение займа равными годовыми выплатами». Решение Величину ежегодного платежа находим из уравнения при Р=5; r = 0,1; n =5; FM4(10%,5)=3,791A=1318,913 Общая сумма выплат составит 51318,913= 6 594 566 руб. Взятый заем может погашаться различными способами. Например, заемщик может создать специальный погасительный фонд и накапливать в нем средства, чтобы погасить заем одним платежом в конце срока финансовой операции. Очевидно, что это возможно только в том случае, если у заемщика есть возможность накапливать деньги в некотором фонде под более высокий процент. Пусть заем в сумме Р выдан под r1 сложных ссудных процентов на n периодов. Тогда к конце срока финансовой операции финансовой операции величина займа составит величину  . Платежи в погасительный фонд составляют годовую ренту с ежегодным платежом, равным А и процентной ставкой r2 > r1, будущая стоимость этой ренты равна величине . Тогда величину ежегодного платежа в погасительный фонд находим из уравнения: Задача 6. Создание погасительного фонда Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. У заемщика есть возможность создать накопительный фонд в банке, начисляющим по вкладам 12% годовых. Найти величину ежегодного платежа в погасительный фонд. Решение Величину ежегодного платежа в погасительный фонд находим из формулы при P=5; r1=0,1;r2=0,12;n=5A=1267550 Величина ежегодного платежа в погасительный фонд равна 1 267 550 руб. Общие расходы по погашению займа составят (1 267 550 ∙5)= 6 337 749 руб. Задачи для подготовки к занятию Задача 1. Кредит в размере К = 400 тыс. руб., выданный на год под простую ссудную ставку 20% годовых, должен погашаться четырьмя платежами в конце каждого квартала. Долг погашается равными выплатами, т.е. в каждый квартал погашается 100 тыс. руб. основного долга. Определить величину каждой квартальной выплаты, состоящей из погашаемой ¼ части основного долга и процентов с суммы задолженности за соответствующий квартал. Задача 2. Кредит в сумме 100 млн.руб. выдан на 5 лет под 20% годовых. Для погашения кредита создается погасительный фонд, на который начисляются проценты по ставке 22% годовых. Фонд формируется в течение 5 лет, взносы производятся в конце каждого года равными суммами. Необходимо найти размер срочных выплат. Задание на практическое занятие 13. Практическое приложение финансовых вычислений Контрольные вопросы
Задача 1. Кредит в размере 900 тыс. руб. взят на 4 года под ставку 5% годовых. Составить план погашения кредита равными годовыми выплатами. Задача 2. Фирма взяла в банке кредит в сумме 100 млн. руб. на 3 года под 30% годовых. Рассчитать все возможные схемы погашения кредита. Результаты расчетов занести в таблицу:
Задача 3. Банк выдал долгосрочный кредит в сумме 40 тыс. долл. на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. Начисление процентов производится раз в году. Составить план погашения займа. Задача 4. Фирма получила кредит 5 млн. руб. на 4 года под 8% сложных годовых в банке А. Кредитный контракт предусматривает погашение долга разовым платежом. Одновременно с получением кредита фирма начала создавать погасительный фонд, для чего открыла счет в банке Б. На размещенные средства банк Б начисляет 10% годовых. Определить ежегодные расходы фирмы по амортизации долга при условии, что в погасительный фонд вносятся ежегодно равные суммы. Задача 5. Долг, выданный на 5 лет под 8% годовых (сложные проценты), равен 80 тыс. долл. Платежи в погасительный фонд должны возрастать на 10% ежегодно. На взносы в погасительный фонд начисляются сложные проценты по ставке 9% годовых. Составить план погашения долга. Задача 6. Кредит, выданный на два года, составляет 500 тыс. руб. Процентная ставка по кредиту равна 18%. Клиенту предоставляется возможность выбора следующих вариантов погашения долга:
Составить план погашения кредита для каждого варианта, определить, какой из вариантов погашения кредита является наиболее выгодным с точки зрения минимизации издержек заемщика. | |||||||||||||||||||||||||||||||||||||||||||||||