лекции по теории вероятности. Лекции по теории вероятностей. Руководство к решению задач по теории вероятностей и математической статистике

• Название: Руководство к решению задач по теории вероятностей и математической статистике
• Анкор: лекции по теории вероятности
• Дата: 07.12.2021
• Размер: 0.61 Mb.
• Имя файла: Лекции по теории вероятностей.doc
• Тип: Руководство; #295399
• страница: 3 из 3

§ 7. Геометрическая вероятность

Пусть - некоторое множество на числовой прямой (на плоскости или в пространстве), имеющее конечную длину (площадь или объем) .

Р ассмотрим все возможные подмножества , имеющие конечную длину (площадь или объем). Ясно, такие подмножества образуют алгебру событий. Введем на этой алгебре вероятность по формуле . Эта вероятность носит название геометрической вероятности и представляет собой вероятность попадания брошенной наугад точки в фигуру S при условии, что эта точка обязательно попадет в .
Пример. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождение причала, если время стоянки обоих пароходов – 2 часа.

Решение. Пусть х и y время прихода пароходов к причалу. Тогда встреча состоится тогда и только тогда, когда .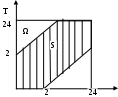


.

§2. Случайные величины
Определение 1. Пусть - вероятностное пространство. Числовая функция X( ), определенная на называется случайной величиной дискретного типа, если она принимает конечное или счетное множество значений , причем множество = являются событиями для всех значений величины X( ).

Определение 2. Функция f( )=P(X= ) называется законом распределения случайной величины Х.

Последовательность 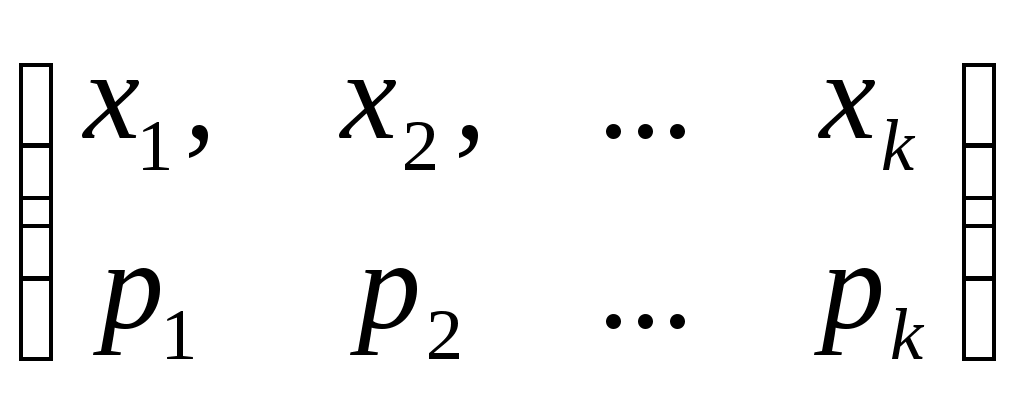, где = f( ) называется рядом распределения случайной величины Х.

График функции = f( ) называется многоугольником (полигоном) распределения вероятностей.

Определение 3. Две дискретные случайные величины и называются независимыми, если события являются независимыми при любых и .

Случайные величины , , …, (n≥2) называются независимыми, если события , , …, независимы в совокупности при любых возможных значениях этих величин.
§3. Числовые характеристики дискретных случайных величин
Определение 1 Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности

.

Для бесконечной случайной величины: .

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно этой величине:

M[C]=C, где С=const.

2. Числовой множитель можно выносить за знак математического ожидания:

M[CX]=C·M[X].

3. Математическое ожидание произведения двух независимых случайных величин Х и У равно произведению их математических ожиданий:

М[XY]=M[X] ·M[Y].

5. 
   Математическое ожидание суммы двух случайных величин Х и У равно сумме их математических ожиданий: М[X+Y]=M[X] +M[Y].
   
6. 
   Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
   

М(X-M[X])=0.

Математическое ожидание любой случайной величины Х представляет собой среднее арифметическое всех возможных значений этой величины.
Определение 2. Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения значений величины от ее математического ожидания:

.

Характеристиками рассеивания возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднеквадратичное отклонение.

Среднеквадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:

.

Дисперсия обладает следующими свойствами.

1. Дисперсияконстанты равна нулю: D[C]=0, где С=const.

2. При увеличении случайной величины в С раз ее дисперсия увеличится в C² раз: D[CX]=C²·D[X].

3. Дисперсия суммы (разности) двух независимых случайных величин Х и У равна сумме из дисперсий: D[X+Y]=D[X] +D[Y].

4. Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания: D[X]=M[X²] – (M[X])².
§4. Основные законы распределения дискретных случайных величин.

1, Дискретная случайная величина Х имеет биномиальный закон распределения, если она принимает значения 0, 1, 2, …, n с вероятностями

m=0,1,…,n, где q=1-p, 0 ≤p≤1. – формула Бернулли.

Теорема1. Математическое ожидание случайной величины Х, распределенной по биномиальному закону равно произведению числа испытаний на вероятность появления события в каждом испытании:

=np.

Теорема 2. Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

D[X]=npq.

Дискретная случайная величина Х имеет закон распределения Пуассона, если она принимает значения 0, 1, 2, …, m… с вероятностями:

(λ>0).

Теорема Пуассона. Закон распределения Пуассона является предельным случаем биномиального закона распределения при , , , т.е. при всех m=0, 1, 2, … при .

(Так как вероятность p в каждом испытании мала, то закон распределения Пуассона называют законом редких явлений).

Теоремой Пуассона можно пользоваться вместо формулы Бернулли, когда n большое число, p- малое и λ=np≤10.

Математическое ожидание случайной величины Х, распределенной по закону Пуассона, равно: = λ.

Дисперсия случайной величины Х, распределенной по закону Пуассона, равна:

D[X]= λ.

Функция распределения случайной величины

Определение 1. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x:

.

Определение 2. Cлучайная величина Х называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Свойства функции распределения

1. 
   Значения функции распределения принадлежат отрезку [0.1]: .
   
2. 
   Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т.е. если х₁< х₂, то F(x₁)≤F(x₂).
   
3. 
   Вероятность того, что случайная величина примет значение, заключенное в интервале (а, в) равна приращению функции распределения на этом интервале:
   
4. 
   
   
5. 
   Если все возможные значения случайной величины Х находятся на интервале (а, b), то F(x)=0 при х≤а и F(x)=1 при .
   
6. 
   , .
   

Определение. Плотность распределения вероятностей непрерывной случайной величины Х называют функцию - первую производную от функции распределения F(x): .

Плотность вероятности существует только для непрерывных случайных величин.

Свойство плотности вероятности непрерывной случайной величины Х.

1. 
   Плотность вероятности – неотрицательная функция, т.е. f(x)≥0.
   
2. 
   .
   
3. 
   Зная плотность распределения, можно найти функцию распределения случайной величины .
   
4. 
   Вероятность попадания непрерывной случайной величины в интервале [а, в] равна определенному интегралу от ее плотности вероятности в пределах от а до в, т.е. .
   

Формулы для математического ожидания и дисперсии непрерывной случайной величины