лекции по теории вероятности. Лекции по теории вероятностей. Руководство к решению задач по теории вероятностей и математической статистике
 Скачать 0.61 Mb.
|
|
§5 Условная вероятность события Пусть 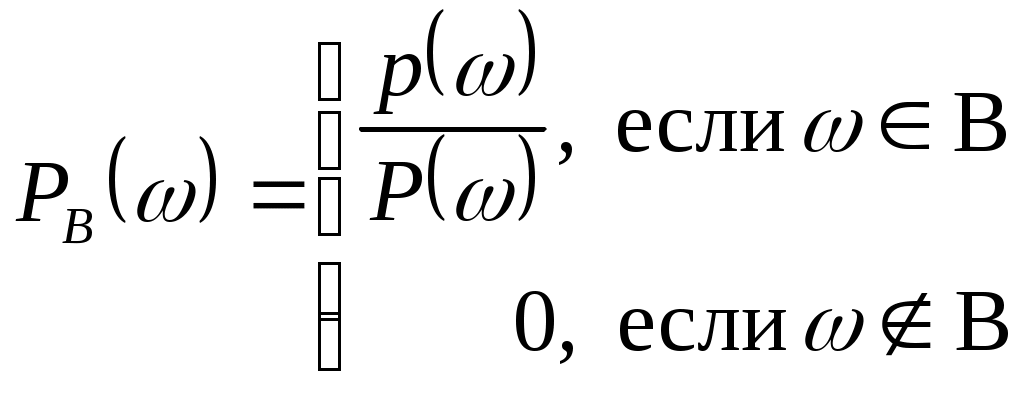 - вероятностное пространство (дискретное) и  произвольное событие из  , удовлетворяющее условию  . Определим на функцию  следующим образом:  .Легко убедиться, что функция  является вероятностью на пространстве . Действительно, первое условие определение вероятности – условие неотрицательности, очевидно, выполняется. Далее, поскольку , то и второе условие определения вероятности у нас выполняется.Определение 1. Функция называется условной вероятностью на , индуцированной событием В.Определение 2. Условной вероятностью события   относительно события называется число  .Основные свойства условной вероятности:  .Действительно, так как  при  , то  . . . Предположим, что элементарные события  равновозможны. Тогда в силу свойства1.  . Отсюда следует, что условная вероятность  представляет собой вероятность события , вычисленную при дополнительном предположении, что произойдет событие В.Примет 1. Брошены две игральные кости. Требуется определить вероятность того, что сумма выпавших на них очков равна 8 (событие А), если известно, что эта сумма есть четное число (событие В). Число всех исходов равно 36. Число исходов, благоприятствующих событию А равно 5. Так как i+j=8 удовлетворяется при i=2, 3, 4, 5, 6 и j=6, 5, 4, 3, 2. Следовательно, вероятность события А равна  . Вычислим теперь вероятность . Так как число исходов (i, j) с четной суммой i+j=18, то  .Пример 2. Из колоды карт последовательно вынуты две карты. Найти вероятность того, что вторая карта будет тузом, если первоначально был вынут туз. Обозначим  {первоначально был вынут туз}, {вторая карта является тузом}. .Пример 3. Вероятность попасть в самолет равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадении в самолет он будет сбит. Обозначим  {попадение в самолет}, {самолет сбит }.Тогда, так как  , то  . Следовательно,  .Теорема умножения вероятностей. Теорема. Вероятность произведения двух событий А и В равна произведению вероятности одного из событий на условную вероятность другого, при условии, что первое произошло:  .Эта теорема непосредственно вытекает из свойства 1 условной вероятности. Определение 2. Событие А независимо от события В, если  .Если А независимо от события В, то В независимо от А, и, следовательно, свойство независимости событий взаимно. Действительно, А независимо от В. Тогда  , т.е. В независимо от А.Пусть события А и В независимы, тогда в силу формулы (1) имеем.  , т.е. вероятность произведения двух независимых событий равна произведению их вероятностей.Свойства независимых событий 1º. Если события А и В независимы, то , обратно, если Если А и В удовлетворяют условию и , то А не зависит от В. 2º. Если А и В независимы, то независимы события  и В,  и Аи и .3º. Если  =  , то А и В независимы и наоборот.Определение 3. События А и В называются независимыми, если .События  (k≥2) называются попарно независимыми, если  , при i j.Определение 4. События  (k≥2) называются независимыми в совокупности, если для любой последовательности событий имеет место равенство  .Формула умножения вероятностей для нескольких событий Для любой последовательности событий справедлива формула  при условии, что  .Пример. Из колоды карт последовательно без возвращения вытаскиваются 3 карты. Какова вероятность того, что все три карты тузы. Обозначим А={первая карта туз}, B={вторая карта туз}, С={третья карта туз}. Тогда  .§6. Формула полной вероятности и формула Байеса Теорема 1. Пусть  полная группа событий из . Тогда для  события  имеет место формула, называемая формулой вероятности:  .Доказательство. Так как   и события  и  не пересекаются при  , то  .Пример 1. На продажу в магазин поступили однотипные изделия с двух заводов А и В. С завода А поступило 200 изделий, с завода В 800 изделий. При этом 50% изделий, доставленных с завода А, изготовлены в одном из цехов этого завода, 30% в другом и 20 % в третьем. Брак составляет соответственно 1,5%, 2% и 2,5%. Аналогично, 60% изделий, поступивших с завода В, изготовлено в одном цехе, а 40% - в другом. Брак составляет соответственно 1,5%, 2%. Какова вероятность того, что наугад выбранное изделие является дефектным? Решение: Обозначим  {выбранное изделие принадлежит i-му цеху завода В}, i=1, 2, 3. {выбранное изделие принадлежит j-му цеху завода В}, j=1, 2.События  ,  ,  , , образуют полную группу.Следовательно,  , где А ={выбранное изделие является дефектным}. Найдем вероятности, входящие в данную формулу.  ;  ;  ; ;  . ;  ;  ; ;  .Следовательно  .Пример 2. Из колоды карт последовательно без возвращения вытаскивается 3 карты. Какова вероятность того, что 3-я карта будет тузом, если известно, что первая карта является тузом. Обозначим  {вторая карта туз},  {вторая карта не туз}.Тогда  . ;  ;  ;  . Следовательно,  .Теорема 2. Пусть 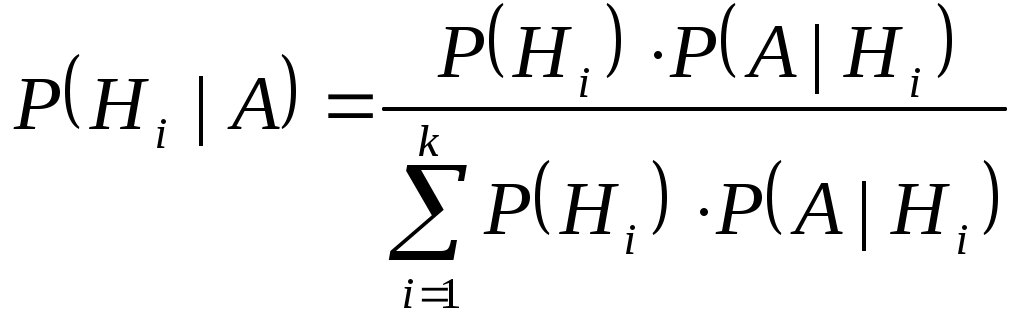образуют полную группу событий из . Тогда имеет место формула Байеса: , i=1,..,k. Пример 1. Два стрелка независимо друг от друга делают по одному выстрелу по общей мишени. Вероятность попадания в мишень для первого стрелка равна 0,8, а для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что эта пробоина принадлежит первому стрелку? Обозначим {первый стрелок попадет в мишень }, {второй стрелок попадет в мишень}, А={в мишени будет обнаружена одна пробоина}.Имеем,  . Так как  , то  Следовательно с учетом того, что  и  получаем  ;  .Пример 2. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру равна 0,6, к 2-му – 0,4. Вероятность того, что годная деталь будет призвана стандартной первым контролером, равна 0,94, а вторым -0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер. Решение. Обозначим 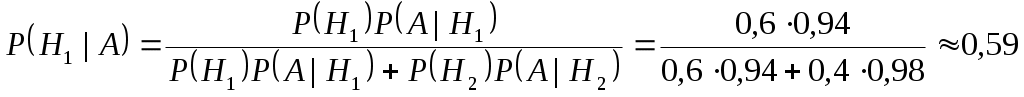{деталь проверил первый контролер}, { деталь проверил второй контролер}, А={деталь признана стандартной}. . |