Расчет неопределенности. ДП Оценивание неопределённости измерений. Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения
 Скачать 478.73 Kb. Скачать 478.73 Kb.
|
Приложение АМЕТОДИКА РАСЧЕТА НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЯ МАССОВОЙ ДОЛИ ВЛАГИ В МОЛОКЕ И МОЛОЧНЫХ ПРОДУКТАХ ПО ГОСТ 3626–73 1. Назначение Настоящий документ устанавливает методику расчета неопределенности измерений массовой доли влаги в молоке и молочных продуктах по ГОСТ 3626–73 п. 2. 2. Измерительная задача Метод измерения. Сущность метода определения массовой доли влаги в молоке и молочных продуктах основана на высушивании навески исследуемого продукта при постоянной температуре. Оборудование и средства измерений. При проведении измерений используются следующие средства измерения и оборудование: весы лабораторные 2-го класса точности Sartorius ВР-300S с допускаемой погрешностью ±0,0006 г. 3. Модель измерения и источники неопределенности Результат измерения массовой доли влаги рассчитываю формулам: 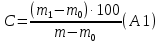 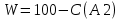 где C − массовая доля сухого вещества, %; W − массовая доля влаги в испытуемом образце, %; m0 − масса бюксы с песком и стеклянной палочкой, г; m − масса бюксы с песком, стеклянной палочкой и навеской исследуемого продукта до высушивания, г; m1 − масса бюксы с песком, стеклянной палочкой и навеской исследуемого продукта после высушивания, г. Модельное уравнение запишем в следующем виде: 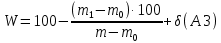 где δ – повторяемость определения массовой доли влаги, %; Величины, входящие в модель измерения, являются источниками неопределенности. Все входные данные с указанием применяемых условных обозначений, единиц измерений, в которых они будут оцениваться, их фактические значения, показатели точности приведены в таблице А1. Таблица А1 – Входные данные
4. Результат измерения Массовую долю сухого вещества (C) вычисляют по формуле (A1). За результат принимают среднее арифметическое двух параллельных определений, расхождение между которыми не должно превышать 0,2 % (для мороженого, сыра, творога и творожных продуктов). Массовую долю влаги вычисляют по формуле (A1), используя среднее значения сухого вещества. 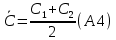 5. Анализ входных величин Входные величины и их стандартные неопределенности представлены в таблице А2. Таблица А2 – Анализ входных величин
6. Анализ корреляций Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах. 7. Суммарная и расширенная неопределенность Воспользуемся методом статистического моделирования Монте-Карло. В программе Excel создадим следующую таблицу: 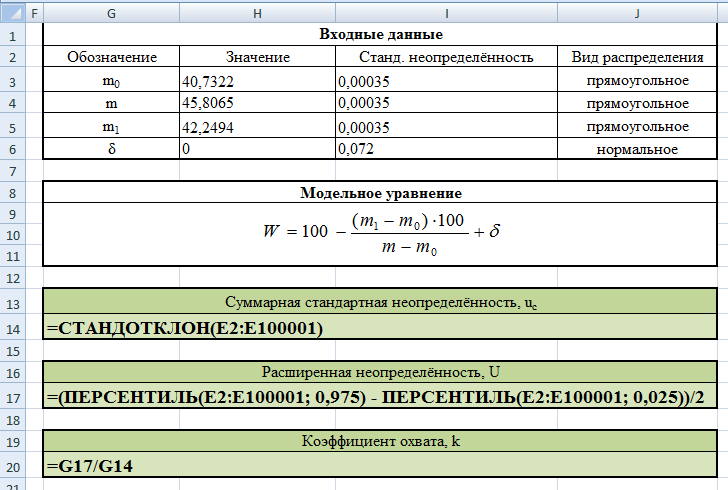 В ячейки A2-E2 внесём следующие формулы:
В столбцах A-E по 100001 строку заполним ячейки формулами по образцу строки 2. Результат вычислений представлен ниже:
8. Представление неопределенности, в зависимости от результата измерений. Входная величина, от которой зависит результат анализа, – m1 (масса бюксы с песком, стеклянной палочкой и навеской исследуемого продукта после высушивания). Варьируя её значения от 40,783 до 45,755 г, найдём расширенную неопределённость, полученные данные сведём в таблицу и построим график зависимости неопределённости от массовой доли сухого вещества.
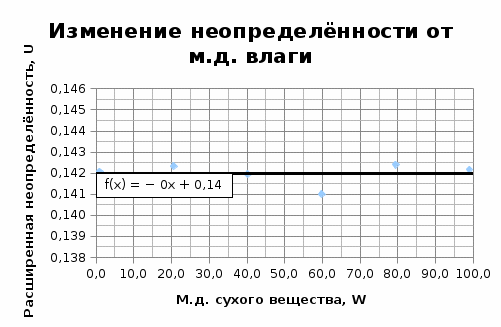 Регрессионное уравнение у = -4∙10-7x+ 0,142 отражает зависимость расширенной неопределённости от значения массовой доли влаги в диапазоне от 1,0 до 99,0 %. Отбрасывая малозначимое слагаемое -4∙10-7x и учитывая, что результат исследования округляется до одного знака после запятой, примем расширенную неопределённость U=0,2 % (округляем в большую сторону). 9. Полный результат измерения. Полный результат измерения влаги в молоке и молочных продуктах по ГОСТ 3626–73 п. 2 записывается в следующем виде: 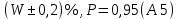 где W –значение массовой доли влаги, % 0,2 – расширенная неопределённость при коэффициенте охвата k= 2 и уровнем доверия Р=0,95. Стр. из | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||