Расчет неопределенности. ДП Оценивание неопределённости измерений. Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения
 Скачать 478.73 Kb. Скачать 478.73 Kb.
|
ПроцедураОбщие положения. Понятия «погрешность» и «неопределенность».Одним из ключевых положений ГОСТ ISO/IEC 17025-2019 является требование к испытательным лабораториям оценивать неопределенность измерений. В случае если хорошо известный метод испытаний устанавливает пределы значений основных источников неопределенности измерений и указывает форму представления результатов вычислений, то считается, что лаборатория выполнила требования оценке неопределённости измерений. Одновременно в большинстве аттестованных методик измерений, используемых при испытаниях, в качестве показателей точности определены приписанные показатели качества на основе характеристики погрешности. Это обусловлено тем, что концепция неопределённости используется сравнительно недавно в нашей стране. Вместе с тем существует определённая связь между этими двумя концепциями статистической оценки результатов измерений. Что бы уяснить её, рассмотрим базовые основы теории. Фундаментальным понятием классической теории измерений является погрешность: 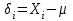 (1) (1)отклонение результата измерения Xi от истинного значения измеряемой величины μ. Погрешность возникает из-за несовершенства процесса измерений. Хотя погрешность не может быть точно известна (из-за неизвестности истинного значения), это понятие удобно использовать для статистического описания процесса измерений. Рассмотрим теперь, как определяется неопределенность. Согласно руководству ЕВРАХИМ/СИТАК «Количественное описание неопределённости в аналитических измерениях», неопределенность - это «Параметр, связанный с результатом измерения и характеризующий разброс значений, которые с достаточным основанием могут быть приписаны измеряемой величине. … Этим параметром может быть, например, стандартное отклонение или ширина доверительного интервала». Согласно другим определениям – неопределенность следует рассматривать как «параметр центрированной случайной величины, представляющей собой разность между истинным значением измеряемой величины и результатом измерений, то есть величины, совпадающей по модулю с погрешностью измерений, но противоположной ей по знаку». Другими словами, это параметр распределения величины 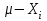 . .Таким образом, различие между традиционным подходом, использующим понятие «погрешность измерений» и подходом «неопределённость» сводится к различию систем координат, относительно которых рассматривают значение измеряемой величины и результат измерений. Из этого следует, что количественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают. Подробнее о соответствии различных форм представления показателей качества написано в РМГ 61-2010. Оценка неопределённости для МВИ с установленной погрешностью.Если результат измерения получен по методу (ГОСТ, ПНД Ф, МУ и т.п.) с установленными границами погрешности, то их значения принимаются равными расширенной неопределённости. 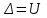 или или 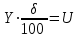 , (2) , (2)где Δ – границы абсолютной погрешности, δ – границы относительной погрешности, Y – результат измерений, U – расширенная неопределённость. Оценка неопределённости МВИ.Метод моделирования для оценки неопределённости измерений.Метод моделирования является наиболее разработанным и широко используемым для оценки неопределенности измерений. Он заключается в установлении модели измерений, которая связывает измеряемую величину с влияющими величинами, расчете стандартной неопределенности каждой влияющей величины и оценке с учетом весовых коэффициентов (коэффициентов чувствительности) стандартной неопределенности измеряемой величины. При использовании этого метода предполагается, что поправки на значимые систематические эффекты включены в модель. Применение закона распространения неопределенности дает возможность оценить суммарную неопределенность, связанную с результатом. Типичными выходными данными подхода моделирования является «бюджет неопределенности», дающий возможность получить итоговую оценку суммарной стандартной неопределенности результата измерения из неопределенностей входных величин. Бюджет неопределенности включает данные о каждой «входной величине» и ее вкладе в результат измерения и неопределенность и сами данные о результате измерения и ее неопределенности, как показано ниже на схеме.
Бюджет неопределенности относится к конкретному результату измерения. Однако разработанный алгоритм расчета бюджета неопределенности можно применить ко всем измерениям, проведенным с использованием того же метода. Для любого нового измерения суммарная стандартная неопределенность u(y) получается путем расчета после введения в алгоритм входных данных xi и u(xi) для этого измерения, на основании которых затем будут получены y и u(y). 1. Описание измерения, составление его модели и выявление источников неопределенности. В значительном числе случаев измеряемая величина Y зависит от N других измеряемых величин Х1, Х2, …, Хm и выражается через зависимость 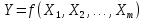 (3) (3)где – X1, X2, …, Xm – входные величины; Y – выходная величина (результат измерения). Входные величины X1, X2, …, XM, от которых зависит выходная величина Y, являются непосредственно измеряемыми и сами могут зависеть от других величин: 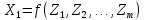 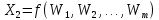 и т.п. (4) и т.п. (4)Описание измеряемой величины в виде функциональной зависимости (математической модели), связывающей измеряемую величину с параметрами, от которых она зависит, называется моделированием. Стадия моделирования является чрезвычайно важной, так как от правильности и тщательности составления модели измерения, которая определяется необходимой точностью, зависит количество источников неопределенности. Источниками неопределенности могут быть пробоотбор, условия хранения, аппаратурные эффекты, чистота реактивов, условия измерений, влияние пробы, вычислительные эффекты, влияние оператора и др. 2. Оценивание значений входных величин и их стандартных неопределенностей. Следующим этапом после выявления источников неопределенности является количественное описание неопределенностей, возникающих от этих источников. Для каждой входной величины необходимо определить ее оценку и стандартную неопределенность. Оценивание неопределенности от каждого источника возможно двумя способами: по типу А (статистически) и по типу В (расчётно). Исходными данными для оценивания стандартной неопределенности по типу А являются результаты многократных измерений 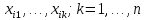 . . На основании полученных результатов рассчитывается среднее арифметическое xi по формуле (5), которое является оценкой входной величины Xi: 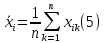 Стандартная неопределенность u(xi) определяется по формуле 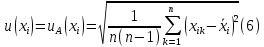 для результата измерения 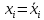 , вычисленного как среднее арифметическое. , вычисленного как среднее арифметическое.Если в МВИ приводятся о повторяемости результатов измерений, то неопределённость выходной величины по типу А можно рассчитать по формуле (для двух параллельных определений): 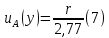 Исходными данными для оценивания стандартной неопределенности по типу В может быть следующая априорная информация: – данные предшествовавших измерений величин, входящих в уравнение измерения; – сведения о виде распределения вероятностей; – данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих средств измерений и материалов; – неопределенности констант и справочных данных; – данные поверки, калибровки, сведения изготовителя о средстве измерения и др. Если оценка xi берется из спецификации изготовителя, свидетельства о поверке, справочника или другого источника, то погрешность обычно задается как отклонение ±a или в виде относительной погрешности δ. Эти данные необходимо перевести в стандартную неопределённость по следующим формулам: 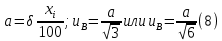 В большинстве случаев отклонение необходимо разделить на 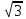 (так называемый равномерный закон распределения вероятностей). Деление на (так называемый равномерный закон распределения вероятностей). Деление на 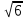 (треугольный закон распределения вероятностей) применяют в том случае, если можно предположить, что определяемая величина скорее находится у заявленного значения, нежели у его границ. В лаборатории это относится к использованию мерной посуды. В некоторых случаях, когда погрешность задана с доверительным интервалом 0,95, её необходимо разделить на 1,96 (нормальный закон распределения вероятностей). (треугольный закон распределения вероятностей) применяют в том случае, если можно предположить, что определяемая величина скорее находится у заявленного значения, нежели у его границ. В лаборатории это относится к использованию мерной посуды. В некоторых случаях, когда погрешность задана с доверительным интервалом 0,95, её необходимо разделить на 1,96 (нормальный закон распределения вероятностей).3. Анализ корреляций. В большинстве случаев проведение данного анализа не требуется. Однако, если есть подозрение, что входные величины испытывают одинаковое воздействие (к примеру измерение двумя термометрами температуры водяной бани), то следует провести анализ корреляций. Для этого вычисляют коэффициент корреляции r, который может принимать значения от -1 до 1. На практике вычисление этого коэффициента проводят в программе «Excel», с помощью функции КОРРЕЛ. Для 5 пар определений значимым будет являться 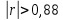 . .4. Вычисление вклада неопределённости входной величины в неопределённость выходной величины. Вклад неопределённости каждой входной величины u(xi) в неопределённость измеряемой величины u(y) (суммарную стандартную неопределённость) определяют как произведение u(xi) на коэффициент чувствительности ci: 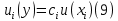 Коэффициенты чувствительности ci показывают, как оценка выходной величины y будет изменяться с изменением входных величин xi. Их находят как частные производные выходной величины по каждой из входных величин: 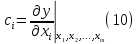 Для модельного уравнения в виде линейной комбинации входных величин вида 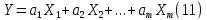 где a1, a2,…, am – постоянные коэффициенты, коэффициенты чувствительности равны коэффициентам при входных величинах: 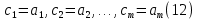 Для модельного уравнения в виде произведения степенных одночленов (напомним, что деление есть возведение в степень -1): 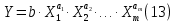 коэффициент чувствительности ci равен отношению измеряемой величины y к значению соответствующей входной величины xi, умноженному на соответствующую степень ai: 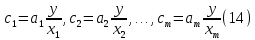 Исходную модель можно разбить на отдельные части, попадающие под модельные выражения, приведённые выше, рассчитать для них неопределённости и потом объединить. 5. Вычисление стандартной неопределенности выходной величины. Вычисление суммарной стандартной неопределённости осуществляется по формуле, называемой законом распространения неопределённости. При отсутствии корреляций между результатами измерения входных величин стандартная неопределённость выходной величины определяется как 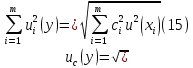 При наличии корреляции в подкоренное выражение вносится дополнительное слагаемое: 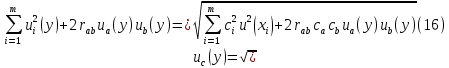 6. Вычисление коэффициента охвата. Коэффициент охвата k представляет собой множитель, на который умножают оценку стандартной суммарной неопределённости uc для получения расширенной неопределённости U. Для большинства применений рекомендуется, чтобы k было равно 2. Однако в тех случаях, когда суммарная неопределенность в большей степени основана на результатах статистических наблюдений (на неопределённости по типу А) с относительно небольшой выборкой (менее шести), то следует вычислить коэффициент охвата. Его расчёт приведён в специализированной литературе. 7. Вычисление расширенной неопределённости. Расширенную неопределённость U получают путём умножения неопределённости выходной величины (суммарной стандартной неопределённости) на коэффициент охвата: 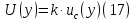 8. Запись полного результата измерения. Полный результат измерения включает в себя оценку выходной величины и приписанное ей значение расширенной неопределённости с указанием уровня доверия 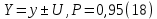 При записи результата следует придерживаться следующих правил: Значение расширенной неопределённости указывается не более, чем с двумя значащими цифрами. Измеренное значение должно оканчиваться цифрой того же разряда, что и округленная расширенная неопределённость. Метод статистического моделирования Монте-Карло для оценки неопределённости измерений.В методе Монте-Карло (ММК) входные величины Х1, Х2, …, Хm представлены как массив случайный чисел, подчиняющихся заданному закону распределения, математическому ожиданию и стандартной неопределённости. Из массивов входных величин получают массив выходной величины Y. Затем по формулам находят расширенную и стандартную суммарную неопределенность, коэффициента охвата. Порядок оценивания расширенной неопределенности с использованием ММК и применением программного обеспечения Excel является наиболее удобным и легко осуществленным. Он заключается в следующих операциях: 1. Формирование массивов данных а) Генерируют L массивов (по количеству входных величин) случайных чисел заданного объема n (n=100000), которые подчиняются необходимым законам распределения. Для этого в программе Excel используют следующие формулы:
в которых необходимо заменить x – на значение входной величины, a – на заданную полуширину, u – на стандартную неопределённость, ν – на число степеней свободы. б) Формируют массив выходной величины, путем подстановки сгенерированных значений входных величин в модельное уравнение. в) Упорядочивают от меньшего к большему (ранжируют) массив выходной величины. 2. Расчет параметров бюджета неопределенности (расширенной и стандартной суммарной неопределенности, коэффициента охвата). По получении массива данных выходной величины определяют: - оценку среднего результата измерения 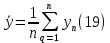 - оценку суммарной стандартной неопределенности результата измерения 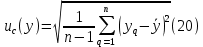 - расширенную неопределенность для заданного уровня доверия 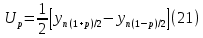 где yn(1+p)/2 и yn(1-p)/2 – соответствующие члены упорядоченного массива данных выходной величины. Для P = 0,95 и n = 105 для расчёта берут 97500 и 2500 член упорядоченного массива выходной величины. - оценку коэффициента охвата 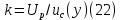 Метод электронных таблиц для вычисления неопределенности.В программе Excel можно реализовать непосредственное вычисление вкладов неопределённости, без определения коэффициентов чувствительности. Для этого используют метод частных приращений. Его суть заключается в использовании формулы: 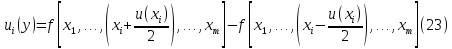 Представление неопределенности, зависящей от результата измерений.В химических измерениях часто наблюдается, что доминирующие вклады в общую неопределенность изменяются примерно пропорционально содержанию аналита в широком диапазоне значений. В таких случаях имеет смысл приводить неопределенность в виде относительной расширенной неопределённости. Если неопределенность не зависит от содержания аналита, то обычно приводят абсолютное значение неопределенности. Чтобы учесть как пропорциональную зависимость, так и возможность примерно постоянного значения неопределенности при изменении содержания, используется следующее общее выражение: 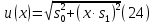 где u(x) – суммарная стандартная неопределенность результата x; s0 – постоянная составляющая неопределенности; s1 – коэффициент пропорциональности. Это выражение основано на обычном методе сложения двух составляющих суммарной неопределенности в предположении, что одна составляющая (s0) является постоянной, а другая (xs1) пропорциональна содержанию. Такой подход применим только тогда, когда можно получить достаточно большое число точек для построения графика зависимости. В действительности в экспериментальных исследованиях нечасто есть возможность набрать большую статистику данных. При таких обстоятельствах адекватное приближение можно получить с помощью простой линейной регрессии, включающей четыре или более значений суммарной неопределенности, полученных при различных концентрациях аналита. В этом случае зависимость задаётся выражением 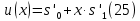 В общем случае, неопределенности могут быть представлены в виде значений s′0 и s′1. Эти значения можно использовать для того, чтобы дать оценку неопределенности в области применения методики. В частных случаях возможны следующие упрощения выражения (25): Неопределенность не зависит от содержания аналита (преобладает слагаемое s′0). При этих обстоятельствах значение s′1 можно принять равным нулю. s′0 представляет собой вычисленную стандартную неопределенность. Неопределенность явно зависит от содержания аналита (преобладает слагаемое s′1). При этих обстоятельствах, а также когда область применения методики не охватывает близкие к нулю содержания, s′0 с достаточным основанием можно принять равным нулю, a s′1 будет просто представлять собой относительную неопределенность. |