Расчет неопределенности. ДП Оценивание неопределённости измерений. Руководство по выражению неопределенности измерения гост р исо 110952007 Статистические методы. Линейная калибровка с использованием образцов сравнения
 Скачать 478.73 Kb. Скачать 478.73 Kb.
|
Практические аспекты оценки неопределённости КХА.Источники неопределенности при проведении КХА.Типичными источниками при проведении количественных химических измерений являются неопределенности оценивания: 1) массы; 2) объема раствора (жидкости); 3) степени чистоты реактива; 4) значения эталонного образца; 5) градуировочной функции; 6) эквивалентного объема титранта; 7) погрешности средств измерений и испытательного оборудования; 8) влияния случайных факторов и др. Более подробное описание каждого из возможных источников и их количественная оценка представлены ниже. 1) Неопределенность оценивания массы. Неопределенность, связанную с нахождением массы анализируемой навески, оценивают исходя из данных о погрешности весов, которые, как правило, приведены в свидетельстве о поверке или калибровке весов или в документации производителя. ПРИМЕР 1. Необходимо оценить стандартную неопределенность массы навески m = 30,2378 г, которую определяли с помощью весов лабораторных модели ВЛР-200г-М 2-го класса точности с пределом допускаемой погрешности Δm = ±0,0005 г. Предполагая равномерный закон распределения погрешности весов, стандартную неопределенность массы вычисляют по уравнению 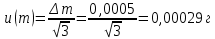 2) Неопределенность оценивания объема жидкости. Объем жидкости, находящейся в мерной посуде, подвержен влиянию двух основных источников неопределенности: калибровка и влияние температуры. ПРИМЕР 2. Необходимо рассчитать стандартную неопределенность объема воды, в котором растворяли навеску вещества, при этом использовали мерную колбу исполнения 1, вместимостью 100 мл, 1-го класса точности (1-100-1 ГОСТ 1770–74). Калибровка. Стандартная неопределенность u(Vk) вычисляется исходя из предположения о треугольном распределении вероятностей отклонения объема от заявленной вместимости. Выбор треугольного распределения, а не прямоугольного (равномерного), обусловлен тем, что технологически, в процессе производства мерной посуды, номинальные значения объёма более вероятны, чем крайние. В данном случае для колбы 1-100-1 ГОСТ 1770–74 допустимая погрешность равна 0,1 мл, а стандартная неопределенность: 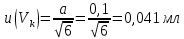 Влияние температуры. Мерную стеклянную посуду калибруют при температуре 20 °С, в то время как температура в лаборатории колеблется в пределах 20±5 °С. Коэффициент объемного расширения воды и, следовательно, водных растворов равен α=2,1·10–4 °С–1. Возможные колебания объема a из-за различия температуры, при которой проводятся испытания, от температуры, при которой калибруется мерная посуда, определяют по формуле 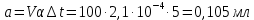 Исходя из прямоугольного распределения вероятностей, стандартная неопределенность, связанная с изменением температуры, составит: 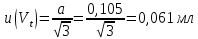 Эти два вклада суммируют, получая стандартную неопределенность объема u(V): 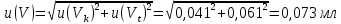 3) Неопределенность оценивания степени чистоты реактива. Стандартную неопределенность чистоты реактива u(P), или неопределенность содержания вещества в реактиве, рассчитывают исходя из информации о степени его чистоты или содержании основного вещества, указанных в сертификате производителя или другой документации. ПРИМЕР 3. Необходимо рассчитать стандартную неопределенность чистоты гидроксида натрия марки х. ч. по ГОСТ 4328–77. Паспортное значение массовой доли основного вещества – 99,8%. В соответствии с ГОСТ 4328–77, допускаемая относительная суммарная погрешность результата анализа ±0,6 % при доверительной вероятности Р = 0,95. Абсолютная погрешность содержания гидроксида натрия составит: 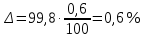 Стандартная неопределенность u(P) рассчитывается исходя из нормального закона распределения (так как известны границы погрешности и доверительная вероятность Р): 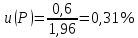 или в неименованных относительных единицах: 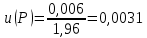 4) Неопределенность оценивания значения эталонного образца. Стандартная неопределенность значения эталонного образца (государственного стандартного образца (ГСО), стандартного образца, аттестованного образца или приготовленного из чистых реактивов) рассчитывается исходя из погрешности аттестации ΔQ. Если образец готовят из стандарт-титра (фиксанала) со строго определенным количеством вещества, то необходимо при оценке неопределенности учесть погрешность содержания вещества и погрешность, вносимую при разбавлении (см. пример 2). Если образец готовят из чистых реактивов, то необходимо учесть чистоту реактива, погрешность взвешивания, а также погрешность объема, вносимую при его растворении (см. примеры 1–3). ПРИМЕР 4. Необходимо рассчитать стандартную неопределенность стандартного образца состава водного раствора этанола с номинальным значением массовой концентрации этанола 2 мг/см3 (ГСО 7969–2001), который имеет границы относительной погрешности 1% (при P = 0,95). Стандартную неопределенность u(Q) рассчитывают исходя из нормального закона распределения (так как известны границы погрешности и доверительная вероятность Р): 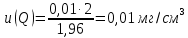 5) Неопределенность оценивания градуировочной функции. Часто в аналитических измерениях концентрацию вещества находят используя градуировочный график. Для этого из стандартных образцов или чистых реактивов готовят градуировочные растворы с известной концентрацией анализируемого соединения (xi) и измеряют их аналитический сигнал (yi). На основании результатов измерений (yi) градуировочных растворов и значений концентрации соединений в растворах (xi) строят градуировочный график, откладывая по оси абсцисс концентрацию соединения в градуировочных растворах хi, а по оси ординат – соответствующее измеренное значение отклика yi. Уравнение градуировочной характеристики обычно имеет линейный вид: 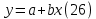 где a – точка пересечения градуировочного графика с осью ординат; b – угловой коэффициент линейного градуировочного графика. Коэффициенты a и b находят методом наименьших квадратов (МНК). Удобнее всего для этого использовать программу Excel и её функцию ЛИНЕЙН. Для этого необходимо заполнить столбцы значениями x и средних значений y. Затем выделить две смежных ячейки и в строке формул ввести следующую формулу: =ЛИНЕЙН(B1:B5;A1:A5) и нажать «Crtl + Shift + Enter». В ней B1:B5 – это диапазон значений y, A1:A5 – диапазон значений x. В первой выделенной ячейке будет рассчитанное значение b, во второй – a. Полученная линейная градуировочная зависимость используется затем для вычисления концентрации xизм в исследуемом растворе, по полученным результатам измерения yизм: 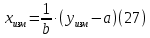 При нахождении неопределенности концентрации (xизм) рассматривают следующие основные источники неопределенности: а) случайные эффекты, результатом которых являются погрешности приписанных исходных значений концентраций градуировочных растворов xi; б) случайные колебания при измерении y, которые оказывают влияние как на отклики при градуировке yi, так и на измеряемый отклик yизм. Оценивание неопределенности u(xизм, x), обусловленной неопределенностями приписанных исходных значений концентраций градуировочных растворов xi, проводится в зависимости от того, каким образом осуществлялось приготовление градуировочных растворов (примеры 1–4). Оценивание неопределенности u(xизм, y), обусловленной случайными колебаниями величины y, можно осуществить разными способами. Рассмотрим способ, основанный на данных градуировки. 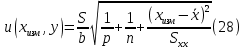 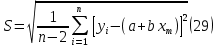 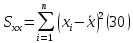 где S – остаточное стандартное отклонение; p – число параллельных измерений исследуемой пробы; n – общее число измерений при построении градуировки; m – индекс, соответствующий номеру градуировочного раствора; 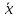 – среднее значение концентрации градуировочных растворов. – среднее значение концентрации градуировочных растворов.Расчет суммарной стандартной неопределенности определяемой концентрации соединения в испытуемом растворе u(xизм) осуществляется суммированием неопределенностей, оцененных исходя из указанных двух источников: 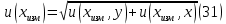 ПРИМЕР 5. При градуировке получены следующие значения:
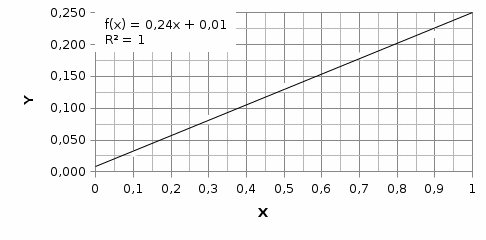 Методом наименьших квадратов найдены коэффициенты градуировочной зависимости: b= 0,2410, a= 0,0087. При этом 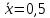 , число градуировочных уровней m = 5, а общее число измерений n = 15. , число градуировочных уровней m = 5, а общее число измерений n = 15.Рассчитаем неопределённость для xизм = 0,26 мг/дм3, полученного как среднеарифметическое двух измерений. 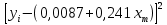
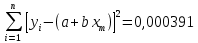 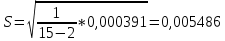 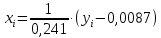
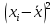
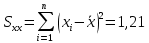 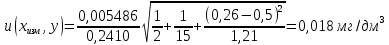 6) Эквивалентный объем титранта. Эквивалентный объем жидкости, пошедшей на титрование, подвержен влиянию трех основных источников неопределенности: калибровка бюретки, воздействие температуры и смещение в результате визуального установления конечной точки титрования. ПРИМЕР 6. Необходимо рассчитать стандартную неопределенность эквивалентного объема гидроксида натрия Vэ = 22 мл, пошедшего на титрование раствора соляной кислоты. Для титрования использовали бюретку типа 1, исполнения 3-го, 2-го класса точности вместимостью 25 мл, с ценой деления 0,1 мл (1-3-2-25-0,1 ГОСТ 29251–91). Калибровка. Стандартная неопределенность эквивалентного объема титранта, возникающая из-за отклонения бюретки 1-3-2-25-0,1 ГОСТ 29251–91 от номинальной вместимости (а = 0,1 мл) при ее изготовлении 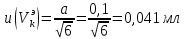 Влияние температуры. Возможные колебания эквивалентного объема титранта а из-за отличия температуры, при которой проводятся испытания, от температуры, при которой калибруется бюретка, определяют по формуле 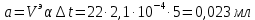 Исходя из равномерного распределения вероятностей значений эквивалентного объема титранта в указанном интервале стандартная неопределенность 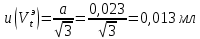 Визуальное установление конечной точки титрования. Если вместо системы автоматического титрования, которая определяет точку эквивалентности по форме рН-кривой, используют индикатор для визуального установления конечной точки, то появляется смещение. Изменение цвета индикатора происходит в некотором диапазоне рН, что приводит к избыточному объему титранта и смещению результата титрования по сравнению с установлением конечной точки с помощью рН-метра. Избыточный объем титранта равен объему одной капли и для данной бюретки составляет 0,05 мл. Исходя из равномерного распределения вероятностей значений избыточного объема титранта в указанном интервале стандартная неопределенность 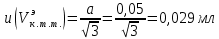 Эти три вклада суммируют и получают стандартную неопределенность эквивалентного объема u(Vэ): 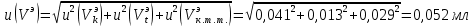 7) Погрешность средств измерений и оборудования. Источниками неопределенности является погрешность средств измерений и оборудования, используемого для создания условий испытаний. Информацию о погрешностях можно найти в свидетельстве о калибровке средств измерений, свидетельстве об аттестации испытательного оборудования, паспорте или другой документации. При проведении измерений с помощью стрелочных приборов, а также контрольно-измерительных мер и приборов (линейка, штангенциркуль и т. д.) неопределенность включает в себя помимо погрешности средства измерения вклад из-за погрешности оператора при снятии показаний со шкалы средства измерения. Погрешность оператора при снятии показаний со шкалы средства измерений может не учитываться, если проводятся повторные измерения одной и той же величины и вычисляется неопределенность типа А. В этом случае погрешность отсчитывания попадет в число случайных отклонений, охватываемых неопределенностью типа А. ПРИМЕР 7. Необходимо рассчитать стандартную неопределенность длины образца, которую определяли при помощи линейки 300 ГОСТ 427–75 с ценой деления 1 мм и допускаемой погрешностью ±0,1 мм. Стандартную неопределенность измерения рассчитывают исходя из равномерного закона распределения и пределов допускаемой погрешности измерения ±0,1 мм: 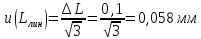 Вклад из-за погрешности оператора при снятии показаний со шкалы линейки также рассчитывается исходя из равномерного закона распределения по формуле 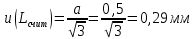 где 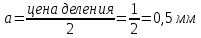 Эти два вклада суммируют, получая стандартную неопределенность измерения длины образца: 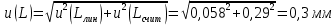 8) Влияние случайных факторов. Влияние случайных факторов при получении параллельных результатов оценивается повторяемостью. Стандартная неопределенность повторяемости ux(повт) оценивается на основании данных среднеквадратического отклонения (СКО) повторяемости. Среднеквадратическое отклонение повторяемости результатов измерений может быть получено из результатов: – нескольких параллельных измерений, выполненных для получения результата измерений в соответствии с МВИ. Расчет СКО повторяемости результата измерения осуществляется по формуле (6). – внутрилабораторного эксперимента, специально организованного с целью оценки СКО повторяемости. Расчет СКО повторяемости осуществляют по формуле (6). – межлабораторных или внутрилабораторных исследований, проведенных с целью оценки точности МВИ при ее разработке. Информация о повторяемости результатов измерений приводятся в МВИ в виде СКО повторяемости (Sr) или предела повторяемости (r) (предел разности нескольких параллельных измерений). В этом случае стандартная неопределенность 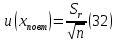 или 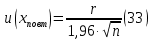 где n – число параллельных измерений; r – предел повторяемости. Для двух параллельных определений формула (33) принимает вид формулы (7) 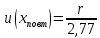 ПРИМЕР 8. Необходимо рассчитать стандартную неопределенность повторяемости при определении концентрации раствора гидроксида натрия NaOH. Известно, что допускаемое расхождение между результатами двух параллельных измерений в одной лаборатории не должно превышать 0,05 моль/л. В данном случае стандартную неопределенность повторяемости можно вычислить исходя из предела повторяемости r = 0,05 моль/л по формуле (7) 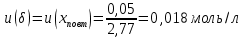 Суммирование неопределённостей.При оценивании неопределенности с целью установления суммарной неопределенности от разных источников необходимо производить суммирование стандартных неопределенностей входных величин. Суммирование в случае отсутствия корреляции входных величин осуществляется с учетом весовых коэффициентов, в качестве которых используют соответствующие частные производные. 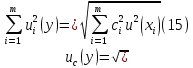 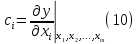 ПРИМЕР 9. Необходимо рассчитать расширенную неопределенность концентрации раствора гидроксида натрия марки х. ч., приготовленного из навески массой m = 30,2378 г и растворенного в 0,1 л. Молярную концентрацию раствора NaOH вычисляют по формуле 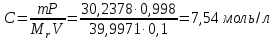 где m – масса NaOH, г; P – степень чистоты NaOH; Mr – молярная масса NaOH, г/моль; V – объем раствора NaOH, л. Стандартная неопределенность концентрации раствора NaOH включает в себя пять вкладов: u(m) – стандартная неопределенность массы NaOH; u(V) – стандартная неопределенность объема, в котором был растворен NaOH; u(P) – стандартная неопределенность степени чистоты NaOH; u(Mr) – стандартная неопределенность молярной массы NaOH (имеет незначительный вклад и поэтому неучитывается); u(δ) – стандартная неопределенность повторяемости. Расчет стандартных неопределенностей u(m), u(V), u(P), u(δ) проводится в соответствии с примерами 1–3, 8. Суммирование стандартных неопределенностей осуществляется с учетом коэффициентов чувствительности, которые рассчитываются как частные производные выходной величины от входной: 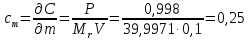 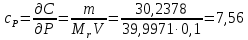 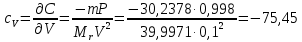 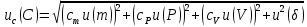 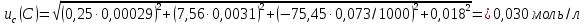 где 0,073/1000 неопределённость объёма переведённая из размерности [мл] в размерность [л]. Расширенная неопределённость при коэффициенте охвата k= 2 и уровнем доверия 0,95: 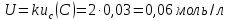 Таким образом, концентрация гидроксида натрия в приготовленном растворе составляет: 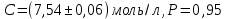 Процентный вклад каждой входной величины в суммарную неопределенность рассчитывается как 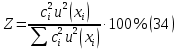
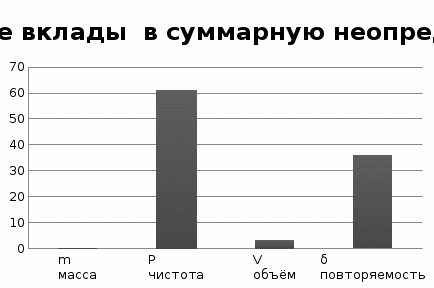 Как видно из гистограммы, наибольший вклад вносит неопределенность, возникающая из-за погрешности объема и случайных факторов. Бюджет неопределенности, в котором отражается основная информация о рассчитанных неопределенностях, представлен в таблице ниже.
Нахождение неопределённости, используя метод Монте-Карло.Воспользуемся методом статистического моделирования Монте-Карло для оценки неопределённость концентрации раствора гидроксида натрия из примера 9. ПРИМЕР 10. Исходные данные для моделирования следующие: - расчётная формула 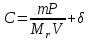 - масса навески гидроксида натрия m=30,2378 г, погрешность взвешивания Δm = ±0,0005 г с прямоугольным распределением; - степень чистоты гидроксида натрия P=0,998, стандартная неопределённость u(P)=0,0031 с нормальным распределением; - молярная масса гидроксида натрия Mr=39,9971 г/моль; - объём раствора V=0,1 л, погрешность определения объёма состоит из двух составляющих: ΔVk=0,0001 л с треугольным распределением и ΔVt=0,000105 л с прямоугольным распределением; - неопределённость связанная со случайными факторами u(δ)=0,018 моль/л. Для характеристики точности взвешивания и измерения объёма взяты характеристики погрешности (полуширины распределения). Это влияет лишь на используемые формулы для генерации массива случайных значений. В программе Excel сгенерируем массив из 100000 случайных значений для каждой переменной. Общий вид формул Excel приведен в разделе 5.3.2, для нашего примера они примут следующий вид:
Создадим файл Excel и заполним ячейки A1, B1, C1, D1 приведёнными формулами. Перейдём на ячейку A100000, затем зажав клавишу «Shift» перейдём на ячейку D1 (произойдёт выделение таблицы из 4 столбцов и 100000 строк). На Главной вкладке в разделе Редактирование выберем Заполнить → Вниз.  Полученный массив данных скопируем, нажав клавиши «Ctrl+C». Создадим новый файл Excel, щёлкнем правой кнопкой мыши по ячейке A1, в появившемся контекстном меню выберем Специальная вставка → Значения.  Тем самым мы перенесли сгенерированный массив данных в новый лист Excel. Файл с генерацией случайных значений больше не нужен. В ячейку E1 введём следующую формулу: =A1*B1/(39,9971*C1)+D1. Заполним ячейки E1:E100000, по аналогии как это было сделано для генерации массива случайных значений. Скопируем столбец E в столбец D, используя специальную вставку значений. Отсортируем значения в столбце D от меньшего к большему. Для этого выделим столбец D и на Главной вкладке в разделе Редактирование выберем Сортировка и фильтр → Сортировка от минимального к максимальному.  В свободном месте таблицы введём следующие формулы: 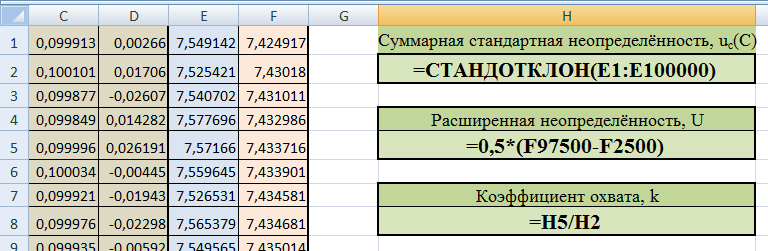 Получаем расширенную неопределённость с уровнем доверия 0,95: 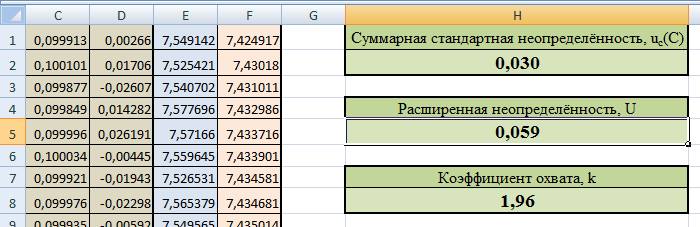 Оценка неопределенности, найденная ММК, совпадает с оценкой неопределённости полученной аналитическим методом. Примечание. Вместо сортировки значений от меньшего к большему и выборкой значений соответствующих границам 97,5% и 2,5% всех значений (ячейки F97500 и F2500), можно использовать функцию Excel ПЕРСЕНТИЛЬ. Тогда формулу для расчёта расширенной неопределённости можно записать в следующем виде: =(ПЕРСЕНТИЛЬ(E1:E100000; 0,975) - ПЕРСЕНТИЛЬ(E1:E100000; 0,025))/2 . Нахождение неопределённости методом частных приращений.В программе Excel можно реализовать непосредственное вычисление вкладов неопределённости, без определения коэффициентов чувствительности. Вклад отдельных составляющих вычисляется по формуле (23): 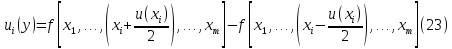 Оценим неопределённость концентрации раствора гидроксида натрия из примера 9. ПРИМЕР 11. Исходные данные для расчёта следующие: - расчётная формула 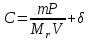 - масса навески гидроксида натрия m=30,2378 г, стандартная неопределенность u(m)=0,00029 г; - степень чистоты гидроксида натрия P=0,998, стандартная неопределённость u(P)=0,0031; - молярная масса гидроксида натрия Mr=39,9971 г/моль; - объём раствора V=0,1 л, стандартная неопределенность u(V)=0,000073 л; - неопределённость, связанная со случайными факторами u(δ)=0,018 моль/л. Заполним таблицу исходными данными и формулами, как показано ниже 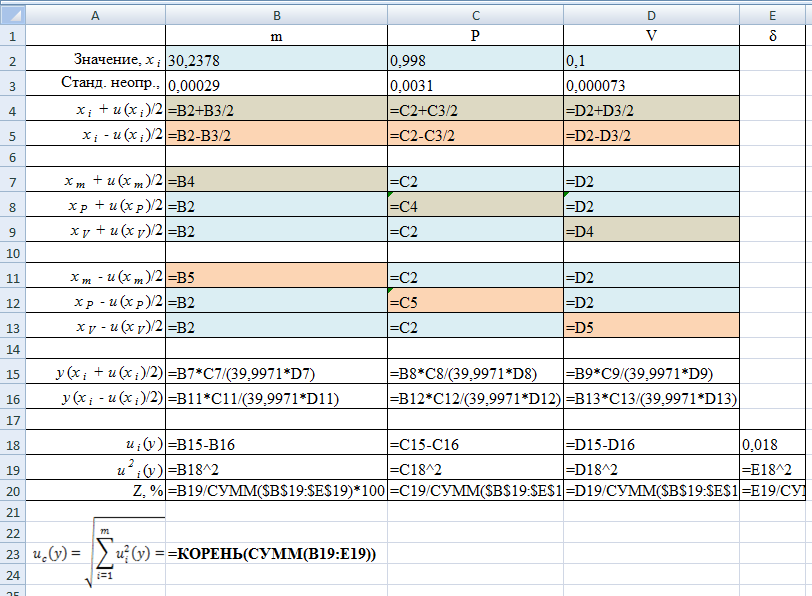 В строках 4 и 5 вычисляются значения переменных скорректированных на половинное значение их неопределённостей (неопределённость, делённая на два, прибавляется или вычитается). В строках 7-9 и 11-13 заполняется матрица значений, где по диагонали представлены скорректированные значения переменных, а в остальных ячейках – исходные значения. В строках 15 и 16 вычисляем концентрацию гидроксида натрия для каждой скорректированной переменной. В строке 18 попарно вычитаем полученные концентрации, тем самым находя вклад каждой переменной в стандартную неопределённость концентрации гидроксида натрия. Извлекая квадратный корень из суммы квадратов всех составляющих неопределённости, получим стандартную неопределённость концентрации гидроксида натрия. Процентный вклад каждой входной величины в суммарную неопределенность рассчитывается в строке 20. 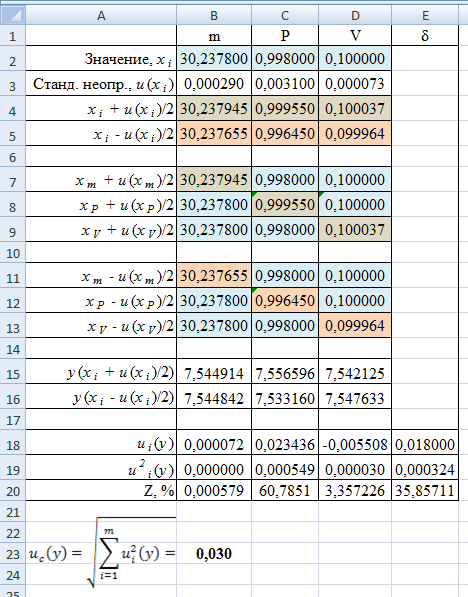 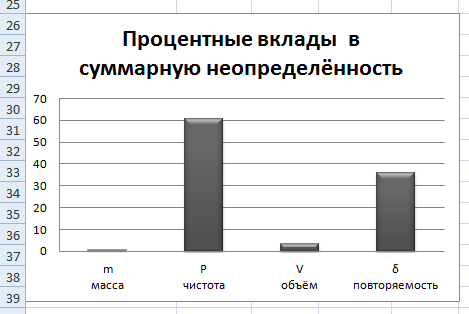 Расширенная неопределённость при коэффициенте охвата k= 2 и уровнем доверия P=0,95 составит: 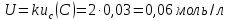 Представление неопределенности, зависящей от результата измерений.Оценим характер зависимости неопределённости от содержания аналита и установим её для широкого диапазона входных значений, на основе примера 10. ПРИМЕР 12. Исходная задача как в примере 10, за исключением массы навески гидроксида натрия, которая варьируется в диапазоне от 25 до 50 г. Найдём расширенную неопределённость для различных навесок гидроксида натрия, полученные данные сведём в таблицу и построим график зависимости неопределённости от концентрации гидроксида натрия.
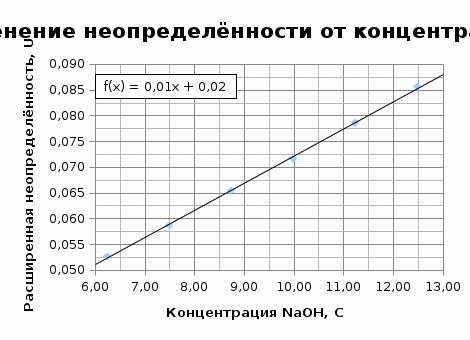 Регрессионное уравнение у = 0,0053x+ 0,0193 отражает зависимость расширенной неопределённости от значения концентрации гидроксида натрия в диапазоне концентраций от 6,25 до 12,5 моль/л. Таким образом, расширенная неопределённость с уровнем доверия Р=0,95, в диапазоне концентраций от 6,25 до 12,5 моль/л составит: 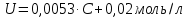 где C – концентрация гидроксида натрия, моль/л. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
