Контрольная работа по математике. С. Е. Царева выделяет следующие этапы решения текстовой задачи
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
     Вопрос №1. В начальном курсе математики рассматриваются простые задачи и составные преимущественно в 2-4 действия. Задача, для решения которой надо выполнить несколько действий, связанных между собой (независимо от того, будут ли это разные или одинаковые действия), называется составной. Для составных задач нет единого основания классификации, которое позволило бы разделить их на группы. Однако в методической литературе из всего многообразия составных задач выделяются некоторые группы, сходные или математической структурой (например, задачи, в которых надо сумму разделить на число), или способом решения (например, задачи, решаемые способом нахождения значения постоянной величины), или конкретным содержанием (например, задачи на движение) и т.п. Особое внимание в начальной школе уделяется обучению решения задач с пропорциональными величинами: на нахождение четвёртого пропорционального, на пропорциональное деление, на нахождение неизвестных по двум разностям. Решение составной задачи сводится к расчленению её на ряд простых задач и к последовательному их решению. Таким образом, для решения составной задачи надо установить систему связей между данными и искомым, в соответствии с которой выбрать, а затем выполнить арифметические действия. Подготовкой к решению составных задач будет умение вычленять систему связей, иначе говоря, разбивать составную задачу на ряд простых, последовательное решение которых и будет решением составной задачи. В методике работы на этой ступени выделяются следующие этапы: 1 этап – ознакомление с содержанием задачи; 2 этап – поиск решения задачи; 3 этап – выполнение решения задачи; 4 этап – проверка решения задачи. С.Е. Царева выделяет следующие этапы решения текстовой задачи: 1. Восприятие и осмысление задачи. 2. Поиск плана решения. 3. Выполнение плана решения. 4. Проверка решения. 5. Формулировка ответа на вопрос задачи (вывода о выполнении требования). 6. Исследование решения. Рассмотрим особенности осуществления каждого из этих этапов в процессе решения составных задач с пропорциональными величинами. Составные задачи на нахождение четвёртого пропорционального. Задача. Мама купила несколько пирожков с капустой по 5 рублей за штуку и столько же пирожков с мясом по 10 рублей за штуку. За пирожки с капустой она уплатила 30 рублей. Сколько стоили пирожки с мясом? а). 1-й этап. Восприятие и осмысление задачи. После прочтения текста задачи учитель в ходе беседы с учащимися обсуждает её условие. Составляется краткая запись в виде таблицы (табл. 1).  б). 2-й этап. Поиск плана решения. На данном этапе можно использовать различные схемы рассуждения: от вопроса к данным, от данных к вопросу. Обсуждение может проводиться устно, а может фиксироваться на доске в виде схем (табл. 2).  в). 3-й этап. Выполнение плана решения. Учитель может указать на форму записи решения. Если это не сделано, то ученик вправе самостоятельно определить её, например (табл. 3):  г). 4-й этап. Проверка решения. Проверку можно осуществить двумя способами. Способ 1. Решение задачи другим способом: 1) Во сколько раз больше стоит пирожок с мясом, чем с капустой? 10 : 5 = 2 (руб.) 2) Сколько заплатили за пирожки с капустой? 60 : 2 = 30 (руб.) Способ 2. Составление и решение обратной задачи (табл. 4). 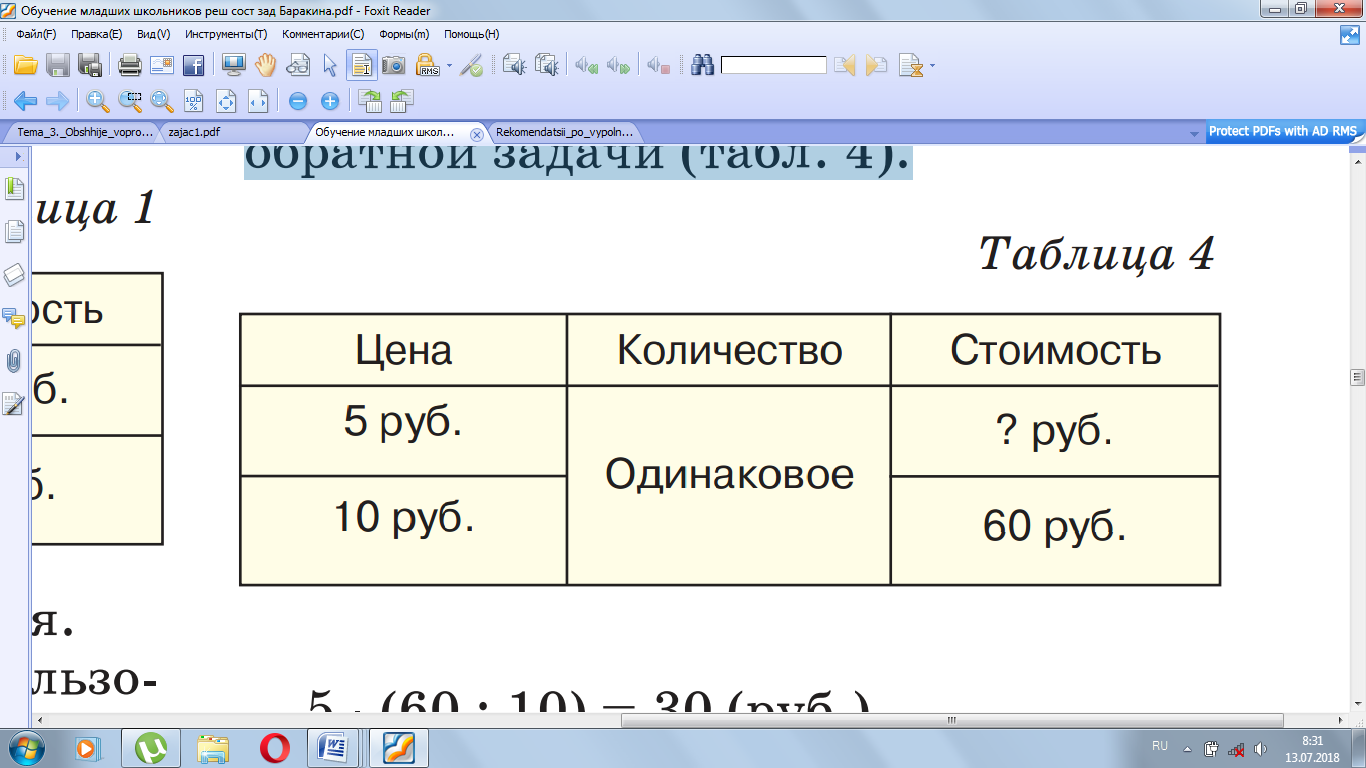 5 .(60 : 10) = 30 (руб.) Вывод: задача решена верно. 5-й этап. Формулировка ответа на вопрос задачи (вывода о выполнении требования). Ответ: 60 рублей стоили пирожки с мясом. 6-й этап. Исследование решения. На данном этапе целесообразно обсудить, какой из найденных способов решения задачи более рациональный, удобный. Вопрос№2. Работа над неравенствами ведется с I класса, органически сочетаясь с изучением арифметического материала. Программа по математике для I-III классов ставит задачу выполнять сравнение чисел, а также сравнение выражений с целью установления отношений "больше", "меньше", "равно"; научить записывать результаты сравнения с помощью знаков Опираясь на операции над множествами и сравнение множеств, учащиеся практически усваивают важнейшие свойства равенств и неравенств (если а>b, то b<а). Неравенства с переменной вида: х+3<7, 10-х>5, х-4>12,72: х<36 вводятся во II классе. Заранее ведется соответствующая подготовительная работа: включаются упражнения, в которых переменная обозначается не буквой, а "окошечком" (квадратом), например: □ >0, 6+4> □, 7+ □ <10 и т.д. Рассматривая во II классе, например, неравенство х+3<10, учащиеся путем подбора находят, при каких значениях буквы х значение суммы х+3 меньше, чем 10. В каждом таком задании дается множество чисел - значений переменной. Ученики подставляют значения буквы в выражение, вычисляют значение выражения и сравнивают его с заданным числом. В результате такой работы выбирают значения переменной, при которых данное неравенство является верным. Позднее в упражнениях с неравенствами значения переменной не даются, учащиеся сами подбирают их. Такие упражнения, как правило, выполняются под руководством учителя. Работая с неравенствами, учащиеся закрепляют представление о переменной и подготавливаются к решению неравенства в IV классе. Изучение уравнений начинается с подготовительного этапа уже в 1 – м классе, когда дети, действуя с предметами, решают такие «задачи» (см. Л. Г. Петерсон «Математика 1», ч. 1, урок 15); ? + = Затем учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в окошке ( см. «Математика 1», ч. 1, урок 20), например: □ + 2 = 7 5 + □ = 7 7 - □ = 2 □ – 5 = 2 Дети находят числа либо подбором, либо на основе знаний состава числа. На данном этапе учителю необходимо включать в устные упражнения следующие задания: - Сколько надо вычесть их 3, чтобы получилось 2? - Сколько надо прибавить к 2, чтобы получилось 4? На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения» (термин «корень» вводится в речевую практику, но внимание на нем не акцентируется) (см. «Математика 1», ч. 3, урок 11). Однако обеспечить пропедевтику такой работы, научить детей подстановке числа вместо буквы в буквенное выражение можно уже в начальной школе. Это сделано, например, в учебнике Л.Г. Петерсон. На данном этапе дети должны понимать, что в записи уравнений в качестве неизвестного числа могут использоваться различные буквы латинского алфавита, например: k + 4 = 7; Р – 3 = 8; Z : 6 = 7 и т. п. Запись решения уравнений сопровождается словесным описанием выполняемых действий. Для выработки правильной математической речи и навыков решения первых уравнений данного вида необходимо использовать таблицы с образцами решений. При решении уравнений учитель должен уделять особое внимание проверке. Так как в старших классах бывает трудно сделать проверку к некоторым уравнениям, следует уже в начальной школе сформировать у детей умение выполнять ее – сначала письменно, а затем уже устно. Уравнения решаются на основе взаимосвязи между частью и целым. При изучении данной темы дети должны научиться находить в уравнениях компоненты, соответствующие целому( сумма, уменьшаемое), и компоненты, соответствующие его частям (слагаемое, вычитаемое, разность). При решении уравнений детям нужно будет вспомнить лишь два известных правила: - Целое равно сумме частей. - Чтобы найти часть, надо из целого вычесть другую часть. На следующем этапе решение уравнений происходит с использованием зависимости между компонентами. В этом случае при нахождении неизвестного числа можно пользоваться приемом замены данного уравнения равнозначным ему уравнением. Опорой перехода может быть граф. Приведу примеры уравнений и замены их равнозначными уравнениями с опорой на графы. 4 х 16 : 4 х 4 = 16 х = 16 4 х = 4 4 4 = 16 : 5 х 7 5 х : 5 = 7 х = 7 5 х = 35 35 : 5 = 7 После того как учащиеся научатся решать простейшие уравнения, включаются более сложные уравнения видов: 48 – х = 16 + 9, а – (60 – 14) = 27, 51 – (х + 15) = 20, решение которых выполняется также на основе взаимосвязи между результатами и компонентами арифметических действий, ведется подготовка к решению задач способом составления уравнений. Несколько иначе это сделано лишь в учебнике Л.Г. Петерсон, где, например, решение уравнений на умножение и деление строится на соотнесении компонентов уравнения со сторонами и площадью прямоугольника и в итоге также сводится к правилам, но это правила нахождения стороны или площади прямоугольника. Уравнения используются для решения задач. Существует правило составления уравнения: 1. Выясняется, что известно, что неизвестно. 2. Обозначение неизвестного за х. 3. Составление уравнения. 4. Решение уравнения. 5. Полученное число истолковывается в соответствии с требованием задачи. Введение записи задачи (о нахождении неизвестной величины) с помощью уравнения начинается с конкретной задачи. Для того, чтобы найти способ решения уравнения, достаточно определить сначала по схеме, а позже и сразу по формуле, чем является неизвестная величина: частью или целым. Если известная величина является целым, то для ее нахождения нужно сложить, а если она часть, то из целого нужно вычесть известные части. Таким образом, ребенку не нужно запоминать правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого.Схема здесь выступает в качестве средства решения уравнения, а уравнение, в свою очередь, как средство решения задачи. В начальной школе в процессе работы над уравнениями закрепляются правила о взаимосвязи части и целого, сторон прямоугольника с его площадью, формируются вычислительные навыки и понимание связи между компонентами действий, закрепляется порядок действий и формируются умения решать текстовые задачи, идет работа над развитием правильной математической речи. На уроках закрепления уравнения позволяют разнообразить виды заданий. Вопрос№3. План изучения темы и время введения 1. Килограмм и литр. – 1 класс. 2. Грамм. – 2 класс. 3. Центнер, тонна. – 3 класс. 4. Обобщенная таблица единиц массы. Формирование понятия массы Первые представления о том, что предметы имеют массу, дети получают в жизненной практике. Взяв в руки предметы, дети могут выяснить, какой легче, а какой тяжелее. Но это можно сделать только в случае явного различия масс. Легко показать, что, сравнивая эти предметы «на руку», можно ошибиться. Этим обосновывается необходимость использования рычажных весов для правильного ответа на вопросы: что легче? что тяжелее? одинаковы ли? В 1 классе с помощью рычажных весов проверяется правильность сравнения масс предметов. Учитель предлагает учащимся сравнить с помощью весов массы портфеля и двухкилограммовой гири; книги и килограммовой гири и т.д. Схематическое изображение весов можно затем использовать так же, как и линейку, для совершенствования вычислительных навыков. Например, используется плакат, в который можно вставлять различные разновесы. Практическое задание может быть таким: выяснить, сколько весит буханка хлеба, ведро картофеля и т.д. Эти данные можно использовать при составлении задач. При этом полезно рассматривать задачи, иллюстрирующие процесс взвешивания. "На одной чаше весов стоит ящик с яблоками, на другой - две гири по 5 кг. Найти массу яблок, если масса ящика 1 кг". Такие задачи вырабатывают у детей практические навыки. Во 2 классе происходит знакомство с граммом. Название этой единицы измерения уже известно детям, учитель только формирует наглядное представление о грамме. С этой целью детям демонстрируют различные виды весов и разновесы к ним. Показывают гирьки в 1г, разновес из гирь до 100 г. При практическом взвешивании с точностью до грамма, действиями с полученными результатами дети углубляют свои знания нумерации в 1000. Хорошим наглядным пособием является циферблат весов, на котором кг разбит на сотни г, десятки г и единицы г. Учащиеся сопоставляют массу гирь 100 г, 200 г, 300 г, 10 г, 20 г, 30 г с показаниями стрелки циферблатных весов, учатся взвешивать на этих весах сыпучие предметы. С помощью аптекарских или лабораторных весов определяют массу. В 3 классе происходит знакомство с центнером и тонной, их соотношением с кг, составляется обобщенная таблица единиц массы. Новые понятия «центнер» и «тонна» можно иллюстрировать различными примерами: масса автомобиля «Запорожец» – 1 т, масса двух мешков картофеля, двух мешков сахара – 1 ц, масса всех учащихся класса – 1 т (если в классе 30-35 человек). В классе вывешивается сводная таблица мер массы: 1 т = 1000 кг, 1 т = 10 ц, 1 ц = 100 кг, 1 кг = 1000 г. Ученики используют ее при выполнении преобразований и сравнении величин: 1) выразите в килограммах 2 т 6 кг, 8000 г; в граммах – 1 кг 25 г; в центнерах – 6 т 9 ц, 8 000 кг; в тоннах – 570 ц; 2) сравните: 12 т и 1 200 кг; 3 200 г и 32 кг; 4 т 8 ц и 480 кг; 220 ц и 20 т 2 ц. Рычажные весы можно применять для иллюстрации понятия уравнения. Например: определить массу предметов, изображенных на рисунке. 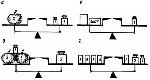 Методика знакомства с емкостью В 1 классе учащиеся сравнивают емкость или вместимость различных сосудов. Вначале сравнение проводится на глаз (сосуды значительно отличаются по своей емкости). Например, предлагается сравнить, куда войдет воды больше: в банку или в кастрюлю. Перед учащимися ставятся пол-литровая банка и кастрюля емкостью 2-3 л, измеряется, сколько банок воды входит в кастрюлю. Тема "Литр" изучается в концентре "Десяток". Выявляя имеющийся у учащихся опыт, учитель предъявляет и стандартные банки вместимостью 1 л, 2 л, 3 л. Учитель выясняет также, знают ли учащиеся, какими мерами измеряют объем молока, бензина, растительного масла, вообще жидкости. Затем он показывает детям литровую кружку, бутылку, банку, наливает воду в кружку, а затем поочередно переливает воду из нее в бутылку и банку. Так учащиеся подводятся к выводу, что в банку вмещается столько же воды, сколько в кружку, и столько же, сколько в бутылку, т.е. равное, одинаковое количество воды – 1 л. Далее учащиеся учатся измерять вместимость сосудов и отмеривать заданное количество литров. Учащиеся должны запомнить емкость стандартных, наиболее часто встречающихся в быту сосудов: банки емкостью 0,5 л, 1 л, 2 л, 3 л, 5 л, бидоны емкостью 1 л, 2 л, 3 л, 5 л, 10 л, 20 л, 40 л, ведра емкостью 8л, 10л, 12 л. После того как введена единица измерения емкости, решаются различные практические задачи. Например: "В одном сосуде 5 л, а в другом 3 л. Как сделать, чтобы в сосудах было поровну?" (Из первого сосуда отлить 2 л воды, тогда в каждом сосуде будет по 3 л, или из первого сосуда перелить во второй 1 л воды). Задача решается практически. "В одном сосуде 3 л воды, а в другом на 2 л больше. Что можно сделать, чтобы во втором сосуде воды было больше только на 1 л?" Задача решается практически, но требует от ученика проведения рассуждений, которые должны предопределить, предугадать практический результат. Полезно рассмотреть различные способы решения данной задачи. Начало формы Собственно все задания связаны с практической проверкой предполагаемого результата, но они даны в виде задачи, а поэтому вызывают больший интерес, чем простое измерение количества воды с помощью банки в 1 л. Кроме литровой банки детям можно показать кубик «тысячи» из арифметического ящика, ведь объем 1 л соответствует 1 куб.дм. Дети часто не верят, что в литровую банку и этот кубик помещается одинаковое количество воды или сыпучих продуктов. Можно склеить 1 куб. дм из плотной бумаги и быстро вылить в него воду или пересыпать сыпучие продукты объемом 1 л. По мере ознакомления учащихся с понятием «масса», «объем» выполняются: 1. Упражнения, иллюстрирующие свойства сложения (вычитания) масс, объемов в процессе решения текстовых задач: «В банке 3 л молока, а в бидоне на 4 л больше. Сколько литров молока в бидоне». 2. Упражнения, раскрывающие свойства умножения (деления) массы (величины) на число: «Масса арбуза 4 кг, а тыквы в 3 раза больше. Узнай массу тыквы». 3. Задания, иллюстрирующие возможность деления массы, объема (величины) на величину: «Вместимость 1 банки 3 л. Сколько потребуется таких банок, чтобы разлить 12 л сока?». 4. Задания, направленные на выражение одной единицы измерения массы через другие, являющиеся основой выполнения арифметических действий с величинами. Например: 5 т 380 кг + 4 т 930 кг; 10312 кг = 10 т 312 кг. Вопрос№4. Учащиеся выпускающиеся из начальной школы должны: 1) узнавать на рисунках отрезки, треугольники, четырёхугольники, пятиугольники, круг и окружность; 2) Измерять длину отрезка, строить отрезок заданной длины, сравнивать отрезки; 3) Строить с помощью линейки, циркуля, клетчатой бумаги различные фигуры; 4) Уметь вычислять периметр многоугольника, площадь прямоугольника; 5) знать единицы измерения длины и площади и отношения между ними. Основными задачами изучения геометрического материала в 1-3 классах являются: 1) формирование геометрических представлений; 2) формирование пространственных представлений и развитие воображения, умений наблюдать, сравнивать, абстрагировать и обобщать; 3) выработка у учащихся практических навыков измерения и построения геометрических фигур с помощью измерительных и чертежных инструментов; 4) формирование умений использовать наглядность в приобретении знаний. Точка и отрезок Изучение геометрического материала в начальной школе обычно начинается с изучения точки и отрезка. В других программам и системах обучения учащиеся знакомятся и с такими понятиями, как линия, прямая, кривая линия, луч, ломаная, звенья ломаной, замкнутые и незамкнутые линии. С точкой дети знакомятся на первых же уроках, как только берут в руки карандаш. Понятием отрезка и его длины учащиеся знакомятся во 2 классе. После получения наглядной модели они показывают, какие предметы в классе имеют вид отрезка (указка, край стола, парты и т.д.). После этого чертят отрезок. Отмечают две точки, прикладывая к ним линейку, соединяют их линией и получают отрезок. Многие учителя с отрезком знакомят уже в 1 классе в связи с изображением условия задачи с помощью отрезков. Во 2 классе, после изучения понятия отрезка полезно выполнять следующие упражнения: 1) Отметь на бумаге три точки и соедини их попарно отрезками. Сколько отрезков получится? 2) Какую фигуру образуют построенные отрезки? 3) Отметь на отрезке АВ точку С. Сколько отрезков на полученном чертеже? Из каких отрезков состоит отрезок АВ? В ходе изучения геометрических фигур точка и отрезок приобретают другие свойства: они становятся их вершиной, стороной и др.. При решении задач с взаимопроникающими элементами отрезки становятся общей стороной двух фигур. Многоугольник, угол, круг Учитель демонстрирует модели круга, треугольника, четырехугольника и пятиугольника. Выясняют, что у последних имеются углы: три угла, четыре угла, пять углов. Их называют: треугольник, четырехугольник, пятиугольник. Выясняют, что они имеют не только угол, но и стороны, определяют число сторон и углов, показывают на модели. В 3 классе рассматривают модели треугольника, четырехугольника и т.д. и называют их одним словом многоугольники, т.е. делают обобщение. После введения обозначения точки как "имени", эти фигуры уже называют "именами": отрезок АВ, треугольник АВС, стороны треугольника - АВ, ВС, АС, вершины - угол А, угол В, угол С. После ознакомления с многоугольниками учащиеся в окружающей обстановке называют или показывают предметы, имеющие форму соответствующего многоугольника, показывают углы, стороны, вершины. Первые сведения об углах учащиеся получают в процессе работы с многоугольниками. При получении модели угла учащимся демонстрируем оторванные углы треугольника и выясняем, что угол образуют две стороны и вершина. где соединяются эти стороны. Для ознакомления с прямым углом демонстрируем модели прямоугольника, четырехугольника с тупым и острым углом. Отрываем прямой, тупой и острый углы и сравнением выясняем, что все эти углы разные. После этого сообщаем: "Вот этот угол называется прямым углом (показываю), а эти - непрямые". После этого учащимся рекомендуется самим получить прямой угол с перегибанием листа бумаги неопределенной формы: они дважды перегибают лист бумаги пополам. Учащимся показывается чертежный треугольник с прямым углом и наложением прямого угла на разные углы показывается, как определить прямой угол. Предлагается назвать предметы, имеющие прямой угол. Для закрепления понятия прямого угла предлагаются упражнения: 1) Найдите прямые углы в предложенных многоугольниках (предлагаются модели, чертежи). 2) Начертите треугольник, имеющий прямой угол. После усвоения понятия прямого угла, учащиеся знакомятся с прямоугольником как четырехугольником, у которого все углы прямые. Для закрепления полученных знаний выполняют упражнения в учебнике. Дети находят прямоугольники, установив предварительно с помощью угольника, что все углы у них прямые. После этого учащиеся называют предметы, имеющие форму прямоугольника и обосновывают свои ответы. Построение прямоугольника целесообразно предложить после установления свойства прямоугольника: противоположные стороны прямоугольника равны. Это свойство устанавливается, используя его модель и измерением длины сторон. Построение же выполняется, используя разлиновку тетради или же, если есть возможность, использованием чертежного треугольника с прямым углом. Методика ознакомления с квадратом аналогична методике ознакомления с прямоугольником. В этом случае из предложенных прямоугольников выделяют тот, у которого все стороны равны. Это и есть квадрат. В ходе практической работы с моделями и чертежами прямоугольника учащиеся знакомятся с такими понятиями, как противоположные стороны прямоугольника, диагонали прямоугольника и их свойствами: противоположные стороны прямоугольника равны; диагонали прямоугольника (квадрата) равны и в точке пересечения делятся пополам; диагонали квадрата при пересечении образуют прямой угол. Окружность и круг, как геометрические фигуры, на уроках математики по традиционной программе рассматриваются в 3-м классе. И здесь, используя практическую работу и метод работы с учебником учащиеся усваивают основные термины: окружность граница круга; центр окружности и круга; радиус и диаметр окружности и круга. Задачи с геометрическим содержанием В начальных классах используются следующие виды задач с геометрическим содержанием: 1. Задачи на составление фигур. 2. Задачи на деление фигур на заданные фигуры. 3. Задачи на распознавание геометрических фигур. 4. Задачи на нахождение суммы длин сторон многоугольника (ознакомление с периметром). 5. Задачи на построение с помощью циркуля и линейки. В начальных классах, кроме задач на построение простейших геометрических фигур, в 3-м классе учащимся предлагаются следующие задачи на построение с помощью циркуля и линейки: 1) построение прямого угла и деление отрезка пополам; 2)построение треугольника с двумя равными сторонами; 3)построение треугольника по трем заданным сторонам; 4)построение прямоугольника (квадрата) используя окружность. Вопрос №5. Длина прямоугольного участка 60 м, а ширина в 3 раза меньше. Четвёртая часть площади участка занята овощами. Какая площадь занята овощами? Цель упражнения: закрепить навыки решения уравнения на основе правил о взаимосвязи сторон прямоугольника с его площадью. Методика работы над ним: 1. Выясняется, что известно, что неизвестно. 2. Обозначение неизвестного за х. 3. Составление уравнения. 4. Решение уравнения. 5. Полученное число истолковывается в соответствии с требованием задачи. x ? а b S=a • b - площадь прямоугольника. S Известно, что a=60м; b=a:3м; 1/4 S - занята под овощами. Требуется найти площадь занятую овощами. Пусть 1/4S=x, тогда если S=a • b, то 4x=60•60/3. Составим уравнение: 4x=1200. Решим уравнение: 4x=1200; x=1200:4; x=300 (м²) - площадь занятая под овощи. Ответ: 300 м². Проверка решения: нужно подставить значение x в уравнение, если они равны, то уравнение решено верно. 4•300=1200; 1200=1200. Вывод: задача решена верно. Список литературы:
|
