Контроль качества44. С. Н. Яшин Титова Н. А., Корнилов Д. А

• Название: С. Н. Яшин Титова Н. А., Корнилов Д. А
• Дата: 27.05.2022
• Размер: 0.69 Mb.
• Имя файла: Контроль качества44.docx
• Тип: Учебное пособие; #552313
• страница: 9 из 14

2.4. ДИАГРАММА РАССЕИВАНИЯ

Диаграмма рассеивания (диаграмма разброса) – это точечная диаграмма, где форма множества свидетельствует о взаимосвязи между парами соответствующих переменных. Рассмотрим три основных вида диаграммы разброса, представленные на рис. 2.20.

Рисунок 2.20. Примеры диаграмм разброса: а – положительная корреляция; б – отрицательная корреляция; в – корреляция отсутствует

 

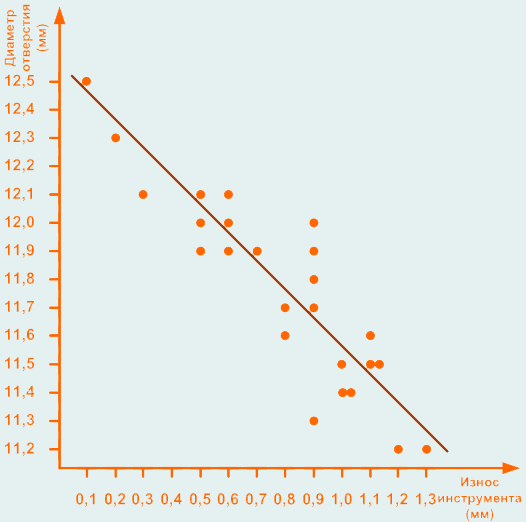
Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению ожидания другой.

Наличие положительной корреляции между случайными величинами означает прямую связь между ними, то есть с ростом одной величины растет и другая. Отрицательная корреляция означает, что с ростом одной из величин вторая уменьшается. Наконец, отсутствие корреляции – отсутствие какого-либо влияния роста одной из величин на другую.

Рассмотрим этапы построения диаграммы разброса.

1. Занести полученные значения пар данных x, y в таблицу для удобства дальнейшего использования. Для получения достоверного результата рекомендуется использовать не менее 30 пар данных.

2. Построить горизонтальную и вертикальную оси. Для удобства прочтения графика рекомендуется выбрать масштаб и диапазон шкал для осей таким образом, чтобы размер рабочих частей осей для отображения полученных значений пар x и yпримерно совпадал. В случае если одна из переменных – фактор, а другая – характеристика качества, рекомендуется для фактора выбрать ось x, а для характеристики качества – ось y.

3. Нанести точки полученных пар значений x и y на график. Если в результате разных наблюдений получены одинаковые пары значений x, y, то отметить эти точки каким-либо знаком или поставьте рядом вторую точку.

4. Сделать вывод.

Для увеличения результативности следует строить и производить сравнение графиков рассеяния, полученных в разные моменты времени.

Рассмотрим пример построения диаграммы разброса. Диаграмма разброса построена для парных данных – «износ инструмента» и «диаметр отверстия». Данные собирались таким образом, чтобы показать влияние износа инструмента на диаметр отверстия.

Результаты измерений представлены в табл. 2.10. Диаграмма разброса представлена на рис. 2.21. Для отображения данных на диаграмме использовался коэффициент масштабирования 10. Между точками на графике можно провести прямую линию, вдоль которой они концентрируются. Это свидетельствует о корреляции между исследуемыми парными данными. Диаграмма разброса показывается величину и наличие взаимосвязи между двумя переменными. Направление и «сжатость» кластера точек говорит о виде и силе взаимосвязи между двумя переменными. Чем больше этот кластер имеет сходство с прямой линией, тем сильнее корреляция между парными данными.

Как и предполагалось, чем больше износ инструмента, тем меньше должен быть диаметр отверстия. На основании проведенного анализа, который предоставляет диаграмма разброса, можно принимать дальнейшие решения. В частности, для приведенного примера можно установить допустимый предел износа инструмента в зависимости от разрешенного допуска на диаметр отверстия.

В практике управления возникают ситуации, при которых необходимо оценить степень взаимосвязи между какими-либо характеристиками или факторами, имеющими количественное выражение. Для этих целей используется коэффициент корреляции. Он может принимать значения от -1 до +1, то есть -1 ≤ r ≤ 1. Положительная корреляция означает прямую связь, то есть при увеличении одной из величин будет увеличиваться и другая. Отрицательная корреляция означает, что при увеличении одной из величин другая будет уменьшаться. Чем больше значение коэффициента корреляции по модулю, тем сильнее взаимосвязь между факторами или величинами.
Таблица 2.10

Результаты измерений износа инструмента и диаметра отверстия

№ измерения	Износ инструмента (мм)	Диаметр отверстия (мм)
1	1,1	11,6
2	1,0	11,5
3	0,9	11,3
4	0,5	12,0
5	0,6	11,9
6	0,9	11,7
7	1,3	11,2
8	1,0	11,4
9	1,1	11,5
10	0,6	12,0
11	0,2	12,3
12	0,9	11,8
13	0,5	11,9
14	1,1	11,5
15	1,0	11,4
16	0,8	11,7
17	0,8	11,6
18	0,5	12,1
19	0,1	12,5
20	1,2	11,2
21	0,7	11,9
22	0,6	12,1
23	0,9	11,9
24	0,3	12,1
25	0,9	12,0

При коэффициенте корреляции, по модулю близком к 1, можно говорить о высокой степени тесноты связи между исследуемыми переменными.

Качественная характеристика связи дается на основе коэффициента корреляции по шкале Чеддока. Эта шкала является довольно условной. Однако благодаря ей становится возможным «перевести» численное (количественное) значение в качественную характеристику (табл. 2.11).

Рисунок 2.21. Диаграмма разброса

Таблица 2.11

Шкала Чеддока

Коэффициент корреляции	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 - 0,9	0,9 – 0,99
Сила связи	слабая	умеренная	заметная	высокая	Весьма высокая

То есть, если в результате расчетов получился коэффициент корреляции, равный 0,7313, то можно сказать, что обнаружена высокая связь.

Если коэффициент корреляции меньше чем на 1% отличается от единицы (составляет 0,99 и больше), то в таком случае говорят об установлении функциональной связи. Если же он отличается менее чем на 10% от нуля, то это говорят об отсутствии какой бы то ни было существенной связи между изучаемыми переменными.

Кроме того, коэффициент корреляции может иметь как положительное, так и отрицательное значение. Интерпретация характера связи в зависимости от значения коэффициента корреляции представлена в табл. 2.12.

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности.